De driehoek van Pascal is een bijzondere wiskundige figuur met heel veel interessante eigenschappen. Het is eigenlijk een opeenstappeling van getallen in een soort piramidevorm. Ook al draagt deze driehoek de naam van de wiskundige Blaise Pascal¹ (1623-1662), deze driehoek en een aantal van zijn eigenschappen waren reeds bekend aan Indische (10e eeuw) en Chinese wiskundigen (11e eeuw). Pascal gebuikte deze driehoek om een aantal kansproblemen op te lossen.

De driehoek wordt rij per rij opgebouwd, van de top naar de basis. Bovenaan de top komt een 1, op de rij eronder komt 1 1 te staan. Elke volgende rij wordt dan als volgt toegevoegd: aan de randen staat steeds een 1 en alle andere getallen in een rij zijn de som van de twee getallen die er net boven staan.

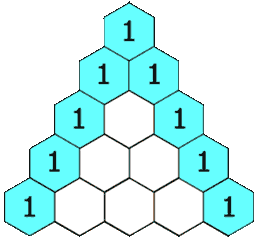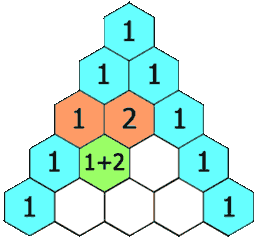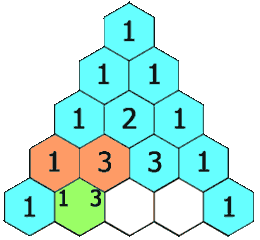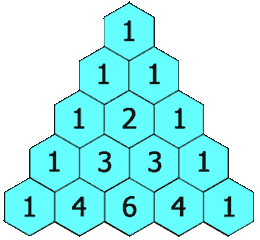
Schrijf een programma dat de driehoek van Pascal op het scherm plaatst. Het programma vraagt eerst aan de gebruiker de ''hoogte'' van de driehoek. De driehoek zelf schrijven we uit als een rechthoekige driehoek (ipv een piramide) waarbij elke rij telkens tegen de kant van het scherm start.

Voorbeeld

Input

De gebruiker geeft eerst de hoogte van de driehoek op:

Ouput

De getallen in elke rij worden op het scherm geschreven, telkens in kolommen met breedte 4

   1
   1   1
   1   2   1
   1   3   3   1
   1   4   6   4   1
   1   5  10  10   5   1
   1   6  15  20  15   6   1
   1   7  21  35  35  21   7   1

Epiloog

Zoals hierboven reeds aangehaald, heeft de driehoek van Pacal heel interessante eigenschappen. Voor de geïntereseerde lezer sommen we er hier een aantal op (zonder bewijs). Merk op dat de rijen van de driehoek steeds vanaf 0 genummerd worden. Dus de top is rij 0.

De som van alle getallen op rij $$n$$ is gelijk aan $$2^n$$.
Als het tweede getal op een rij een priemgetal is dan zijn alle andere getallen op die rij (behalve de 1 aan de randen) ook deelbaar door dit getal.
De tweede getallen op elke rij vormen alle natuurlijke getallen
De derde getallen op elke rij vormen de driehoeksgetallen².
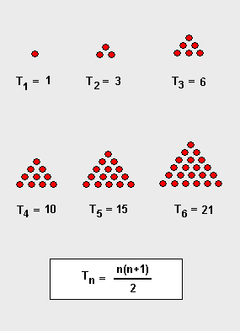
De vierde getallen op elke rij vormen de tetraëdergetallen³.
Als je alle cijfers op rij $$n$$ na elkaar plaatst, krijg je steeds $$11^n$$. Op rij 0 staat $$1=11^0$$. Op rij 1 staat $$11 = 11^1$$. De cijfers op rij 2 vormen $$121 = 11^2$$, enz.
Als je een willekeuig aantal opeenvolgende getallen op een diagonaal, te beginnen bij het getal 1, bij elkaar optelt, dan is de som gelijk aan het getal dat niet op de diagonaal ligt net onder het laatste getal. Men noemt dit het hockeystickpatroon.
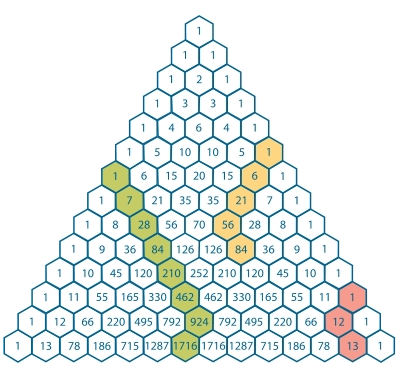
Indien je alle oneven getallen in de driehoek voorstelt met een zwarte stip (en alle even getallen met een witte stip) dan ontstaat een figuur met een fractale structuur: de driehoek van Sierpinski⁴
Indien we de getallen in de driehoek van Pascal ordenen in een rechthoekige driehoek (zoals in het bovenstaande programma), dan vormen de som van de getallen op een schuine diagonaal de Fibonacci-getallen.
Er zijn nog veel meer patronen te vinden in de driehoek van Pascal. Meer patronen en info vind je bijvoorbeeld op https://www.cut-the-knot.org/arithmetic/combinatorics/PascalTriangleProperties.shtml⁵