The sieve of Eratosthenes is an algorithm that dates back to about 240 BC. It can be used to list primes and is one of the oldest methods of its kind. This elegant method is particularly effective when used for smaller primes. However, the method requires keeping a list of all numbers smaller than or equal to a predetermined upper limit $$n$$. This is an increasing disadvantage as the primes to be determined get larger.

Demonstration of the method used in the sieve of Eratosthenes for finding prime numbers smaller than or equal to 120.

The method to find the list of primes that are smaller or equal to a predefined integer $$n$$ works as follows:

make a list of all the numbers from 2 to $$n$$
define $$m$$ as the smallest number from the list
cross out all multiples of $$m$$ in the list, without crossing out $$m$$ itself
define $$m$$ as the next number from the list
continue from step 3, or stop if no next number $$m$$ can be determined

The numbers which were eventually not crossed off are all prime numbers smaller than or equal to $$n$$. This procedure can be sped up in several ways:

in step 4 it is useless to choose a number that has already been crossed off, because all its multiples are already crossed off in the previous steps
you can start with crossing of the multiples of $$m$$ from $$m^2$$. All smaller multiples are already crossed off in the previous steps
if $$m^2$$ is larger than $$n$$, than the procedure can be stopped

Let us clarify the procedure above with an example, in which we seek the prime numbers smaller or equal to $$n = 30$$. We start with a list of 2 until and including 30.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

In the first round we cross off the multiples of $$m = 2$$, starting with $$2^2 = 4$$.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Then we continue crossing of the multiples of $$m = 3$$, starting with $$3^2 = 9$$. Because some numbers can be crossed off multiple times we will now display the multiples of $$m$$ that are crossed off in the next step in green. The numbers displayed in grey are multiples of $$m$$ that are smaller than $$m^2$$. These numbers can be skipped, because they have already been crossed off in the previous steps.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

The number $$m = 4$$ has already been crossed off. We continue crossing off the multiples of $$m = 5$$, starting with $$5^2 = 25$$.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

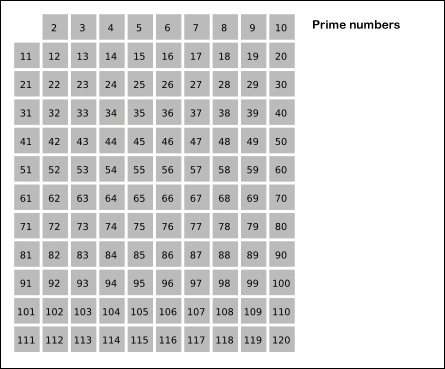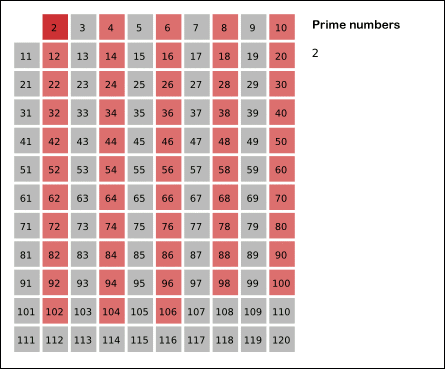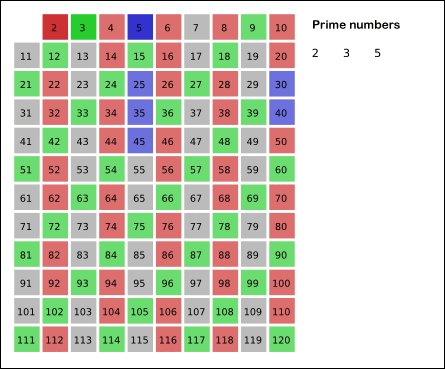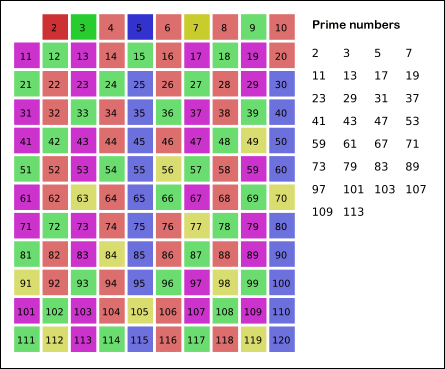
The next number that has not been crossed off yet is $$m = 7$$. We should now cross off the multiples of 7, starting with $$7^2$$. This square, however, is larger than 30, which means the procedure stops here. The result is the prime numbers smaller or equal to $$n = 30$$.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Assignment

Write a function sieve that takes a number $$n \in \mathbb{N}$$. The function must return a sorted list that contains all prime numbers smaller than or equal to $$n$$. The function must implement the sieve of Eratosthenes, including the suggested optimizations that speed up the procedure.

Example

>>> sieve(6)
[2, 3, 5]
>>> sieve(30)
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29]
>>> sieve(100) 
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]