Consider a square $$n \times n$$ grid in which each cell is labeled. Labels are either integers or strings. Cells with the same label form a group. Labeling the cells results in an equidivision if each group has $$n$$ cells and is connected. Two cells are contiguous when they have a common side. A group is connected if all its cells thus form a contiguous unit.

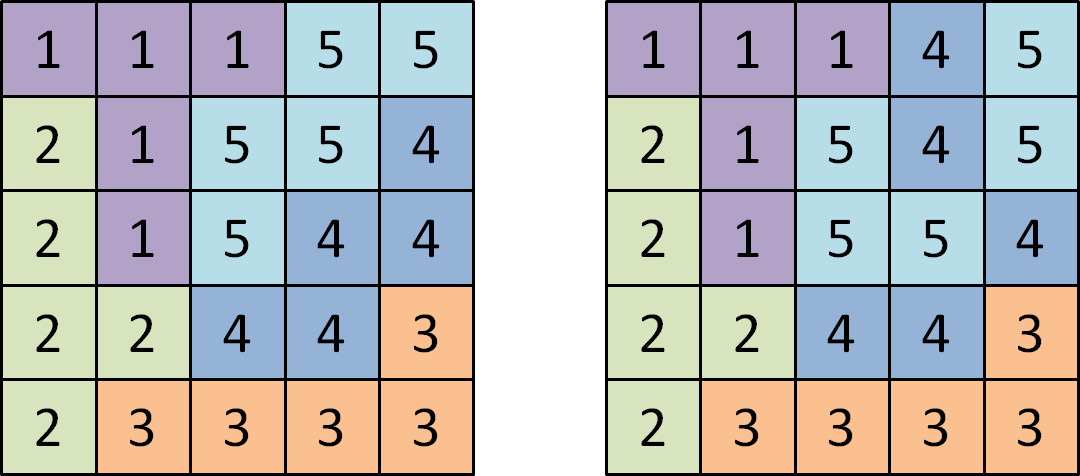
The cells of these two $$5 \times 5$$ grids have been labeled with the integers in the range 1 to 5. All groups have 5 cells, but all groups are connected only in the left grid. The left grid thus is an equidivision, where the right grid is not (groups 4 and 5 are not connected).

Assignment

We represent a square grid of labeled cells as a sequence (list or tuple) containing the rows of the grid, listed from top to bottom. Each row is itself represented as a sequence (list or tuple) containing the labels of the cells on that row, listed from left to right.

The position of a cell in a grid is described by a tuple $$(r, c)$$, with $$r$$ the row number (int) and $$c$$ the column number (int) of the cell in the grid. Rows are indexed top to bottom starting from zero, and columns are indexed left to right starting from zero.

Your task:

Write a function groups that takes a square grid of labeled cells. The function must return a dictionary (dict) that maps each label used in the grid to the set of positions of cells in the grid that carry the label.
Write a function isconnected that takes a collection (list, tuple, set, …) with the positions of the cells in a group. The function must return a Boolean value (bool) that indicates whether the given group is connected.
Write a function isequidivision that takes a square grid of labeled cells. The function must return a Boolean value (bool) that indicates whether the square grid of labeled cells is an equidivision.

Tip

You can make use of a flood fill algorithm for the implementation of the function isconnected.

We start by choosing an element $$e$$ from the collection of points $$S$$. Put that element in a list $$L$$. Here, $$L$$ represents the list of all elements that we have labeled as reachable, but whose neighbors may not have been labeled as such. Remove $$e$$ from $$S$$. Next, we repeat the following procedure until $$L$$ is empty.

choose an element $$f$$ from $$L$$
remove $$f$$ from $$L$$
for all neighbors $$b$$ of $$f$$ in $$S$$
- add $$b$$ to $$L$$
- remove $$b$$ from $$S$$

If $$L$$ is empty, all elements in $$S$$ that are reachable from the element $$e$$ will be removed. If there still are elements in $$S$$, the collection is not connected.

Example

>>> grid = [[1, 1, 1], [2, 2, 3], [2, 3, 3]]
>>> groups(grid)
{1: {(0, 1), (0, 0), (0, 2)}, 2: {(2, 0), (1, 0), (1, 1)}, 3: {(1, 2), (2, 1), (2, 2)}}

>>> grid = [[1, 1, 1, 5, 5], [2, 1, 5, 5, 4], [2, 1, 5, 4, 4], [2, 2, 4, 4, 3], [2, 3, 3, 3, 3]]
>>> groups(grid)
{1: {(0, 1), (0, 0), (0, 2), (2, 1), (1, 1)}, 2: {(3, 0), (2, 0), (1, 0), (3, 1), (4, 0)}, 3: {(4, 1), (4, 4), (3, 4), (4, 3), (4, 2)}, 4: {(3, 2), (2, 3), (2, 4), (1, 4), (3, 3)}, 5: {(1, 2), (0, 3), (1, 3), (2, 2), (0, 4)}}

>>> isconnected({(1, 2), (1, 3), (2, 2), (0, 3), (0, 4)})
True
>>> isconnected({(1, 2), (1, 4), (2, 2), (0, 3), (0, 4)})
False

>>> grid = [[1, 1, 1], [2, 2, 3], [2, 3, 3]]
>>> isequidivision(grid)
True

>>> grid = [[1, 1, 1], [2, 2, 3], [3, 3, 2]]
>>> isequidivision(grid)
False

>>> grid = [[1, 1, 1, 5, 5], [2, 1, 5, 5, 4], [2, 1, 5, 4, 4], [2, 2, 4, 4, 3], [2, 3, 3, 3, 3]]
>>> isequidivision(grid)
True