De formule van Heron is een bijzondere formule waarmee de oppervlakte van een driehoek berekend kan worden aan de hand van de zijden. De formule is genoemd naar Heron van Alexandrië1 die deze bewezen heeft in zijn grote werk Metrica.
De formule voor een driehoek met zijden \(\mathsf{a}\), \(\mathsf{b}\) en \(\mathsf{c}\) is als volgt:
\[\mathsf{A = \sqrt{s \cdot (s-a)\cdot (s-b)\cdot (s-c) } }\]hierbij stelt \(\mathsf{s}\) de halve omtrek voor.
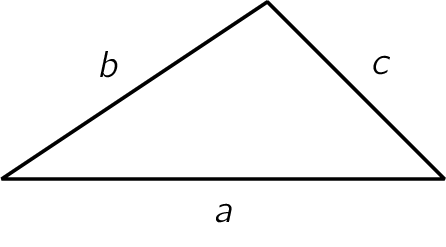
Opgave
Schrijf een functie oppervlakte(a, b, c) die de oppervlakte van een willekeurige driehoek berekent met behulp van de formule van Heron. Rond het resultaat af op 2 cijfers na de komma.
Schrijf eronder een programma dat aan de gebruiker drie getallen vraagt en vervolgens de oppervlakte van de driehoek op het scherm weergeeft.
Voorbeelden
Geeft de gebruiker 4, 13 en 15 in, dan verschijnt er:
De oppervlakte bedraagt 24.0 cm².
de functie werkt hier immers als volgt:
>>> oppervlakte(4, 13, 15)
24.0
Geeft de gebruiker 15, 18 en 20 in, dan verschijnt er:
De oppervlakte bedraagt 129.76 cm².
de functie werkt hier immers als volgt:
>>> oppervlakte(15, 8, 20)
129.76