In his 1986 book The Blind Watchmaker¹, Richard Dawkins says:

I don't know who it was first pointed out that, given enough time, a monkey bashing away at random on a typewriter could produce all the works of Shakespeare. The operative phrase is, of course, given enough time. Let us limit the task facing our monkey somewhat. Suppose that he has to produce, not the complete works of Shakespeare but just the short sentence 'METHINKS IT IS LIKE A WEASEL', and we shall make it relatively easy by giving him a typewriter with a restricted keyboard, one with just the 26 (capital) letters, and a space bar. How long will he take to write this one little sentence?

Then Dawkins suggests that this is a bad analogy for evolution, and proposes the following alternative:

We again use our computer monkey, but with a crucial difference in its program. It again begins by choosing a random sequence of 28 letters, just as before … it duplicates it repeatedly, but with a certain chance of random error — 'mutation' — in the copying. The computer examines the mutant nonsense phrases, the 'progeny' of the original phrase, and chooses the one which, however slightly, most resembles the target phrase, 'METHINKS IT IS LIKE A WEASEL'.

He then describes a computer program that simulates his monkey, which he says took about half an hour to yield the target phrase because it was written in the programming language BASIC². When he rewrote his program in the programming language Pascal³, runtime dropped to eleven seconds.

However, Dawkins overlooked to include the source code of the computer program in his book, nor did he include a formal description of the algorithm used. All the book contains is an output sequence of some of the simulations steps generated by the computer program. To illustrate evolution, Dawkins starts with the phrase

Y YVMQKZPFJXWVHGLAWFVCHQYOPY

New phrases breed from this random phrase. The program duplicates the phrase repeatedly, but with a certain chance of random error — a mutation — in the copying. Every 10th generation is recorded and its (best) result is displayed:

Y YVMQKSPFTXWSHLIKEFV HQYSPY
YETHINKSPITXISHLIKEFA WQYSEY
METHINKS IT ISSLIKE A WEFSEY
METHINKS IT ISBLIKE A WEASES
METHINKS IT ISJLIKE A WEASEO
METHINKS IT IS LIKE A WEASEP

This way, the target phrase

METHINKS IT IS LIKE A WEASEL

was reached in 64 generations. Without a detailed explanation of the algorithm, the procedure for generating these phrases is open for interpretation. Speculations were fueled even more by a fragment in the BBC series Richard Dawkins made about his book, in which a simulation of the computer program is displayed on a computer screen (see video fragment, starting from 4:00).

Assignment

What Richard Dawkins describes in his book, is a forerunner of what today would be called a genetic algorithm⁴. This is a class of meta-heuristics that is routinely used to generate useful solutions to optimization and search problems by using techniques inspired by natural evolution such as inheritance, mutation, selection and crossover. Your task is to implement some of the basic building blocks of a genetic algorithm.

• Write a function fitness that takes two string arguments. In case the strings have a different length, the function must raise an AssertionError with the message strings must have equal length. Otherwise, the function must return an integer that indicates the number of positions in which both strings have the same character.

• Write a function mutation that takes a string argument. The function also has a second optional parameter mutations (default value: 1) that takes an integer $$m \in \mathbb{N}$$. If the given string has length $$n \in \mathbb{N}$$, the function must return a string containing $$n$$ uppercase letters and spaces that differs in exactly $$m$$ positions from the given string. In other words, the given string must have undergone exactly $$m$$ mutations. Make sure all positions have equal probability for a mutation, and that all uppercase letters or the space have equal probability to replace a character at a given position. Of course, it must hold that $$0 \leq m \leq n$$. If this is not the case, the function must raise an AssertionError with the message invalid number of mutations.

• Write a function crossover that takes two string arguments. In case the strings have a different length, the function must raise an AssertionError with the message strings must have equal length. The function also has a third optional parameter point, that takes an integer $$c \in \mathbb{N}_0$$. If the given strings have length $$n \in \mathbb{N}$$, the function must return a tuple containing the two strings that result from crossover of the given strings with crossover point at position $$c$$. This crossover procedure is illustrated in the figure below.

  

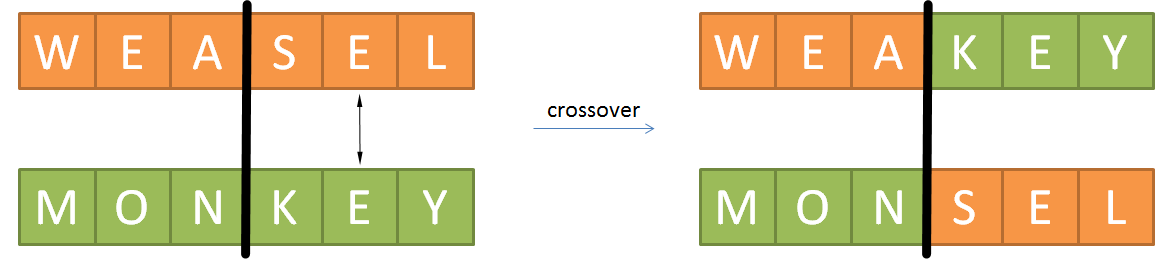
  We put the two strings underneath each other, and after $$c$$ characters we draw a vertical line across both strings. The first string of the tuple is the concatenation of the part of the first given string to the left of the line and the part of the second given string to the right of the line. The second string of the tuple is the concatenation of the part of the second given string to the left of the line and the part of the first given string to the right of the line. It must hold that $$0 < c < n$$. If this is not the case, the function must raise an AssertionError with the message invalid crossover point. In case no value was explicitly passed to the parameter point, a random integer $$c \in \mathbb{N}_0$$ must be drawn from the interval $$0 < c < n$$.

You may assume that all strings passed as an argument to the above functions only contain uppercase letters and spaces, and have length at least 2. There's no need to explicitly check these conditions.

Example

>>> fitness('WEASEL', 'WETSEL')
5
>>> fitness('WEASEL', 'OECYEL')
3
>>> fitness('WEASEL', 'METHINKS')
Traceback (most recent call last):
AssertionError: strings must have equal length

>>> mutation('WEASEL')
'WETSEL'
>>> mutation('WEASEL', mutations=3)
'OECYEL'
>>> mutation('WEASEL', mutations=13)
Traceback (most recent call last):
AssertionError: invalid number of mutations

>>> crossover('WEASEL', 'MONKEY', point=3)
('WEAKEY', 'MONSEL')
>>> crossover('METHINKS', 'AARDVARK')
('MARDVARK', 'AETHINKS')
>>> crossover('WEASEL', 'METHINKS')
Traceback (most recent call last):
AssertionError: strings must have equal length
>>> crossover('WEASEL', 'MONKEY', point=0)
Traceback (most recent call last):
AssertionError: invalid crossover point
>>> crossover('WEASEL', 'MONKEY', point=6)
Traceback (most recent call last):
AssertionError: invalid crossover point