You have three test tubes with a maximum capacity of 3, 5 and 8 units. The first two test tubes are empty, and the third one is filled to the brim with a liquid.
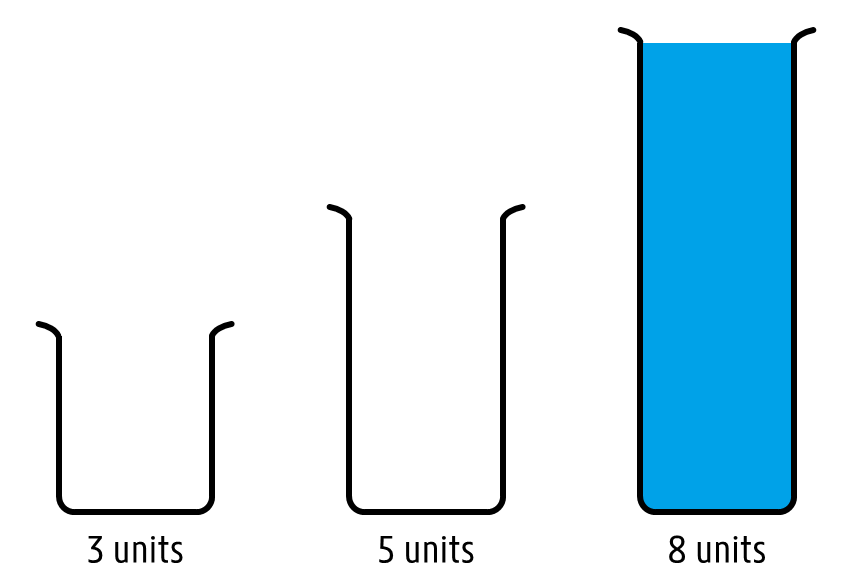
The test tubes have no markings, so it is impossible to accurately measure any quantity of liquid that does not completely fill a test tube. How many steps of pouring liquid from one test tube to another are needed to accurately measure 4 units of liquid, given that no liquid can be spilled and that a single step of pouring liquid from a source test tube into a destination test tube only stops when either the source is empty or the destination is full, whichever happens first?
This diagram shows how to accurately measure 4 units of liquid in 6 steps, which is the smallest number of steps in which this can be achieved. However, there are other possibilities to measure 4 units of liquid in 6 steps.
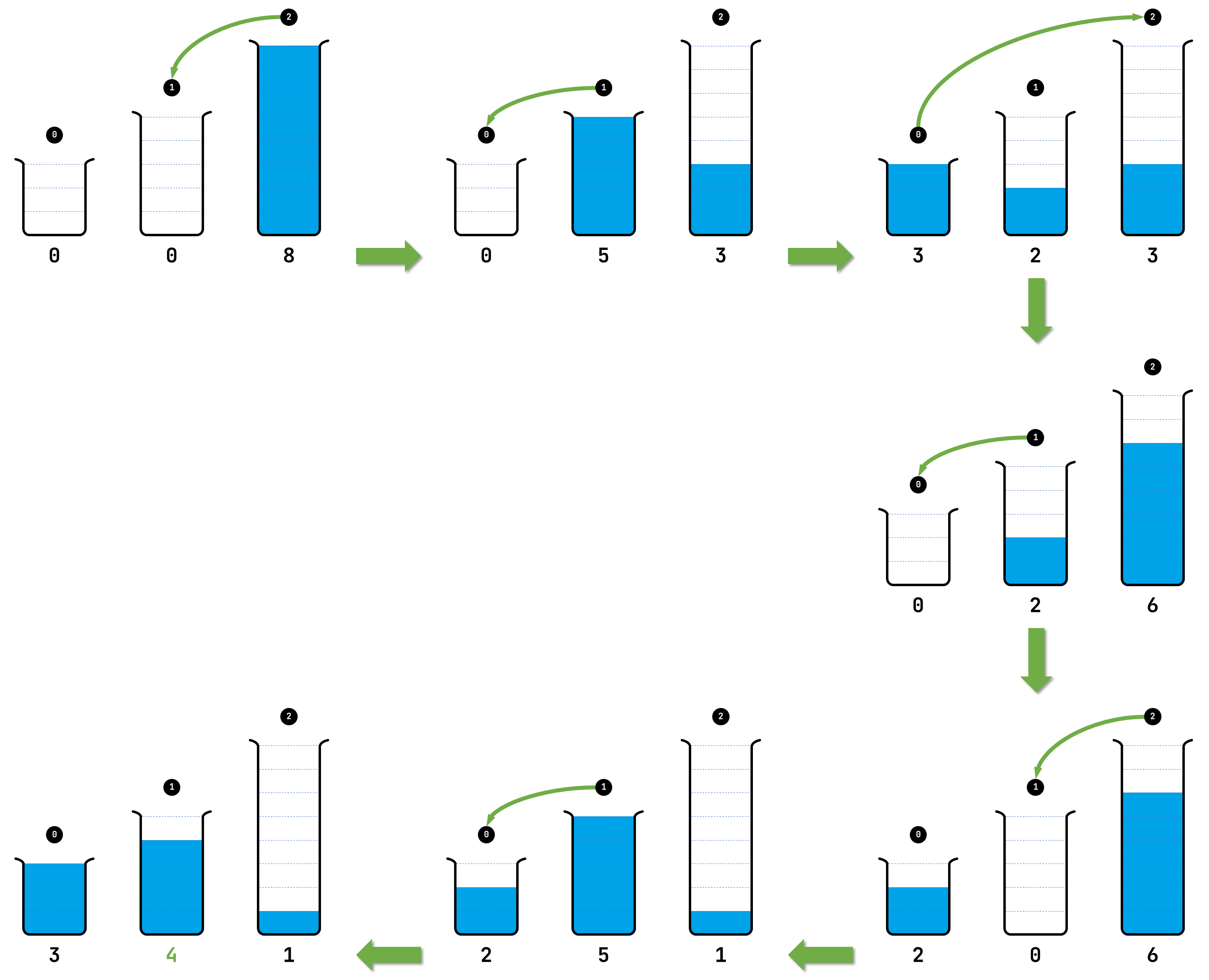
We have provided markings to illustrate that in each step, each test tube contains an integer number of units of liquid. For each step, a thin green arrows points from the source to the destination.
Assignment
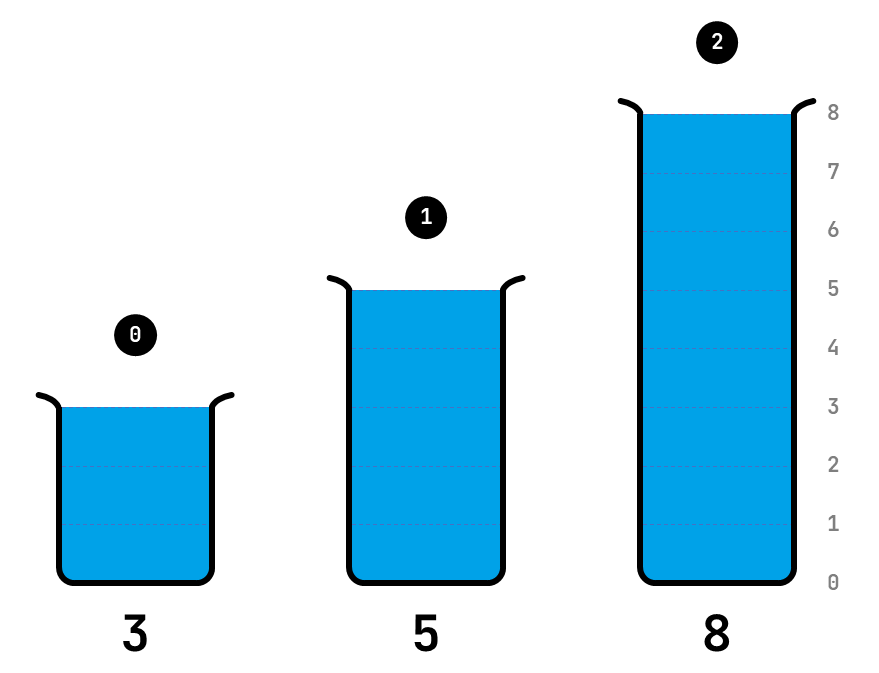
This puzzle can be generalized to $$n \in \mathbb{N}_0$$ test tubes, which we number from left to right, starting with zero. The capacity of the test tubes is described by a tuple $$(c_0, c_1, \ldots, c_{n-1})$$, where test tube $$i$$ may contain at most $$c_i \in \mathbb{N}_0$$ (int) units of liquid ($$0 \leq i < n$$). The state of the test tubes at a given point in time is described by a tuple $$(v_0, v_1, \ldots, v_{n-1})$$, where test tube $$i$$ currently contains $$v_i \in \mathbb{N}$$ (int; $$0 \leq v_i \leq c_i$$) units of liquid ($$0 \leq i < n$$). Thus, the capacity is described as a state in which all test tubes are filled to the brim.
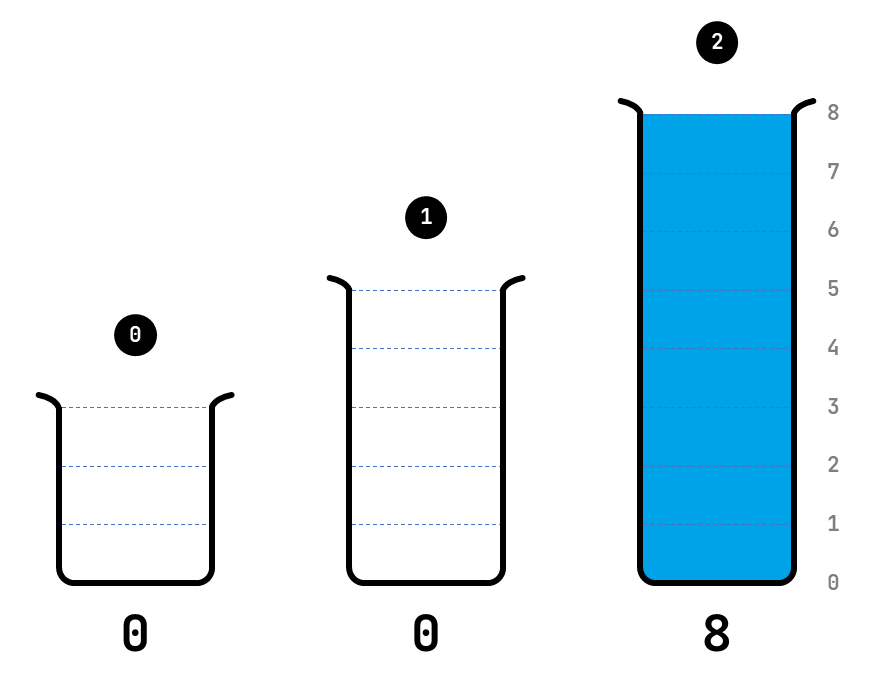
The three test tubes from the puzzle in the introduction have capacity $$(3, 5, 8)$$ and are initially in state $$(0, 0, 8)$$.
There is a standard procedure to find a solution for a generalized puzzle — if such a solution exists. The procedure uses a queue $$Q$$ to keep track of unprocessed states and also remembers the predecessors of all states that were ever added to the queue $$Q$$. The queue $$Q$$ is a list that initially contains only the initial state. A dictionary $$P$$ (dict) is used to keep track of the predecessors by mapping states to their previous state. Initially, dictionary $$P$$ only maps the initial state to the value None, indicating that the initial state has no predecessor.
Each step of the procedure processes state $$p$$ at the beginning of queue $$Q$$. First, state $$p$$ is removed from the beginning of the queue $$Q$$. Then all possible states that can follow state $$p$$ are determined. Such a follow-up state is obtained by pouring liquid from test tube $$x$$ (the source) into test tube $$y$$ (the destination). This is only possible if i) the source $$x$$ and the destination $$y$$ are different test tubes, ii) the source $$x$$ is not empty, and iii) the destination $$y$$ is not full.
The figure below illustrates that initial state $$(0, 0, 8)$$ from the puzzle in the introduction can be followed by states $$(0, 5, 3)$$ and $$(3, 0, 5)$$. On the left, the thin green line indicates that state $$(0, 5, 3)$$ follows after state $$(0, 0, 8)$$ by pouring liquid from test tube 2 into test tube 1. On the right, the thin green line indicates that state $$(3, 0, 5)$$ follows after state $$(0, 0, 8)$$ by pouring liquid from test tube 2 into test tube 0. For all other combinations of a source and a destination, no liquid can be poured in state $$(0, 0, 8)$$.
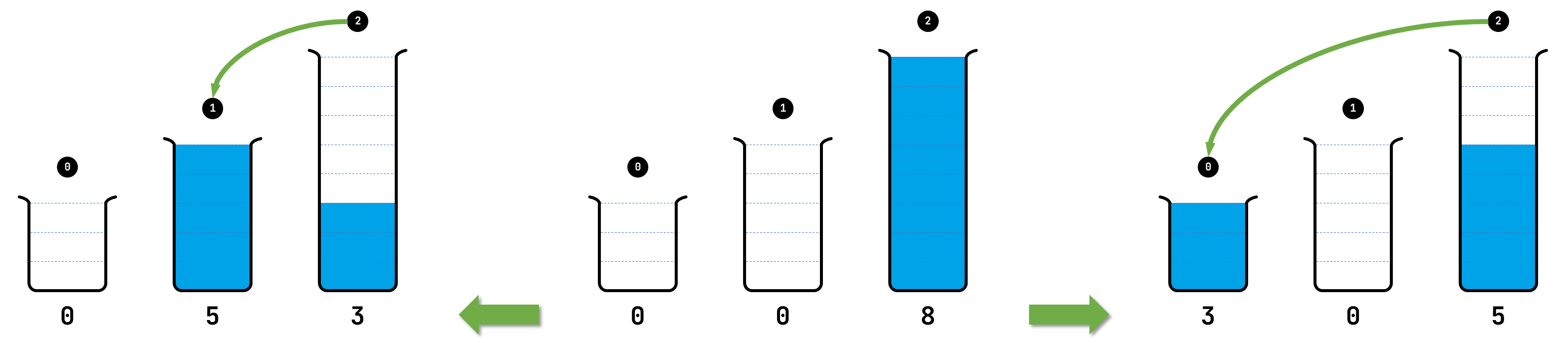
Finally, all of the states that can follow state $$p$$ are processed in increasing order: this order is determined by first comparing the volume of liquid in the test tubes at position $$0$$, and comparing the volume of liquid in the test tubes at position $$x + 1$$ as long as the test tubes at position $$x$$ contain the same volume of liquid. For each follow-up state $$s$$ that has never been added to queue $$Q$$ before, we add state $$s$$ to the end of the queue and remember that state $$s$$ follows state $$p$$ by mapping $$s$$ onto $$p$$ in dictionary $$P$$.
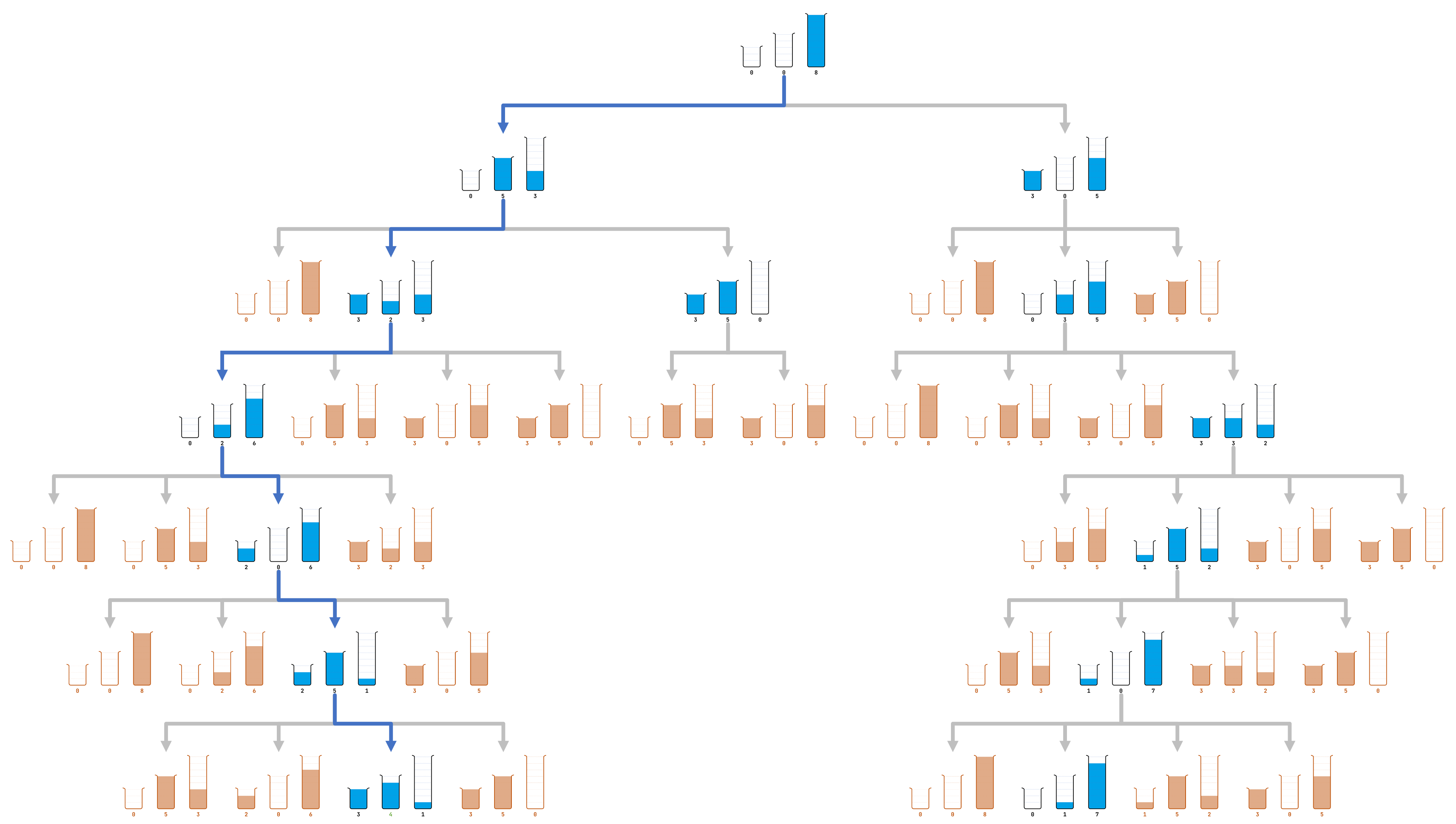
Below we show the progress of the standard procedure on the test tubes from the puzzle in the introduction. The initial state $$(0, 0, 8)$$ is at the top of the tree structure. Arrows connect each state with all their possible follow-up states. Those arrows are tracked in dictionary $$P$$. The order in which the states are added to and removed from the queue $$Q$$ is obtained by visiting the blue states in the tree structure in the usual reading order: from left to right and from top to bottom. The follow-up states that are not processed further — and thus are not added to the queue $$Q$$ again — are colored orange in the three structure.
For the test tubes from the puzzle in the introduction, this table contains for the successive steps the standard procedure goes through i) the state at the head of the queue that is processed, ii) its follow-up states, and iii) the actions that are performed on the queue. Next states are colored orange if not further processing is needed because they were added to the queue in a previous step. States that are discarded from the head of the queue, are crossed out and colored red. States added to the end of the queue are colored green.
| state | follow-up states | queue |
|---|---|---|
| - | - | (0, 0, 8) |
| (0, 0, 8) | (0, 5, 3) (3, 0, 5) | (0, 0, 8) (0, 5, 3) (3, 0, 5) |
| (0, 5, 3) | (0, 0, 8) (3, 2, 3) (3, 5, 0) | (0, 5, 3) (3, 0, 5) (3, 2, 3) (3, 5, 0) |
| (3, 0, 5) | (0, 0, 8) (0, 3, 5) (3, 5, 0) | (3, 0, 5) (3, 2, 3) (3, 5, 0) (0, 3, 5) |
| (3, 2, 3) | (0, 2, 6) (0, 5, 3) (3, 0, 5) (3, 5, 0) | (3, 2, 3) (3, 5, 0) (0, 3, 5) (0, 2, 6) |
| (3, 5, 0) | (0, 5, 3) (3, 0, 5) | (3, 5, 0) (0, 3, 5) (0, 2, 6) |
| (0, 3, 5) | (0, 0, 8) (0, 5, 3) (3, 0, 5) (3, 3, 2) | (0, 3, 5) (0, 2, 6) (3, 3, 2) |
| (0, 2, 6) | (0, 0, 8) (0, 5, 3) (2, 0, 6) (3, 2, 3) | (0, 2, 6) (3, 3, 2) (2, 0, 6) |
| (3, 3, 2) | (0, 3, 5) (1, 5, 2) (3, 0, 5) (3, 5, 0) | (3, 3, 2) (2, 0, 6) (1, 5, 2) |
| (2, 0, 6) | (0, 0, 8) (0, 2, 6) (2, 5, 1) (3, 0, 5) | (2, 0, 6) (1, 5, 2) (2, 5, 1) |
| (1, 5, 2) | (0, 5, 3) (1, 0, 7) (3, 3, 2) (3, 5, 0) | (1, 5, 2) (2, 5, 1) (1, 0, 7) |
| (2, 5, 1) | (0, 5, 3) (2, 0, 6) (3, 4, 1) (3, 5, 0) | (2, 5, 1) (1, 0, 7) (3, 4, 1) |
| (1, 0, 7) | (0, 0, 8) (0, 1, 7) (1, 5, 2) (3, 0, 5) | (1, 0, 7) (3, 4, 1) (0, 1, 7) |
There are two possible cases where the procedure stops. If the queue $$Q$$ no longer contains any states, the procedure can no longer take a next step and it follows that the requested volume of liquid cannot be measured accurately with the test tubes. If state $$p$$ at the beginning of the queue $$Q$$ has a test tube containing the requested volume of liquid, then we can use dictionary $$P$$ to reconstruct (backwards) the path from the initial state to state $$p$$. This path describes how we can measure the requested volume of liquid with the smallest number of pourings possible, and is therefore a solution to the puzzle.
For the test tubes from the puzzle in the introduction, the figure above shows that state $$(3, 4, 1)$$ is the first state that appears at the head of the queue with a test tube containing 4 units of liquid. The blue arrows show the path from the initial state $$(0, 0, 8)$$ to state $$(3, 4, 1)$$ that describes the solution for the puzzle found by the standard procedure: \[ (0, 0, 8) \longrightarrow (0, 5, 3) \longrightarrow (3, 2, 3) \longrightarrow (0, 2, 6) \longrightarrow (2, 0, 6) \longrightarrow (2, 5, 1) \longrightarrow (3, 4, 1)\]
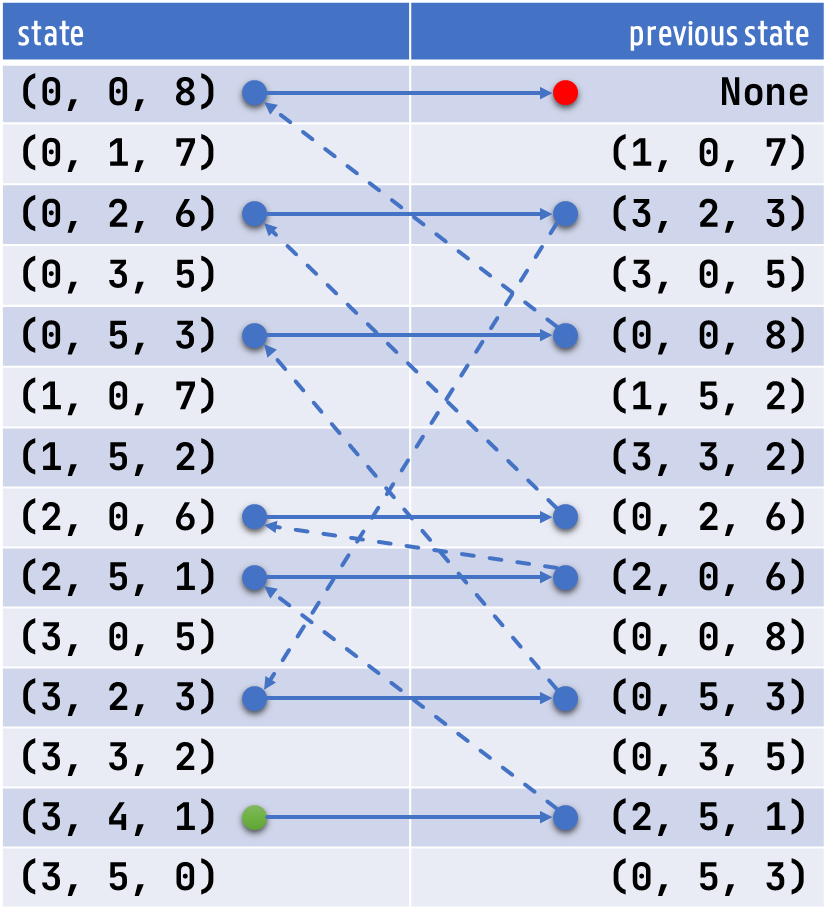
These are the contents of dictionary $$P$$ when state $$(3, 4, 1)$$ appears at the head of the queue while performing the standard procedure on the test tubes from the puzzle in the introduction. The blue arrows indicate how the path from initial state $$(0, 0, 8)$$ to state $$(3, 4, 1)$$ can be reconstructed backwards by starting at state $$(3, 4, 1)$$ (green circle) and repeatedly looking up the previous state up to the initial state, which no longer has a previous state (red circle).
Your task:
-
Write a function pour that takes four arguments: i) a state $$p$$ of test tubes, ii) the capacity $$c$$ of the test tubes, iii) the number $$x$$ of a test tube (the source) and iv) the number $$y$$ of a test tube (the destination). If pouring liquid from the source $$x$$ into the destination $$y$$ is not possible in state $$p$$, then the value None must be returned. Otherwise, the state of the test tubes must be returned after liquid was poured from the source $$x$$ into the destination $$y$$ in state $$p$$, where pouring only stopped when either the source was empty or the destination was full, whichever happened first.
-
Write a function next_states that takes a state $$p$$ of test tubes and the capacity $$c$$ of the test tubes. The function must return a set containing all states that could follow state $$p$$ after pouring liquid from a test tube into another test tube.
-
Write a function step that takes three arguments: i) a queue $$Q$$ (list), ii) a dictionary $$P$$ (dict) with predecessors and iii) the capacity $$c$$ of the test tubes. The contents of queue $$Q$$ and dictionary $$P$$ describe a point in time while applying the standard procedure to solve a test tube puzzle. The function may assume that the queue $$Q$$ is not empty, without the need to check this explicitly. The function must perform a single step of the standard procedure, discarding state $$p$$ from the head of the queue $$Q$$ and processing all states that could follow state $$p$$ as prescribed by the procedure. When performing the step, queue $$Q$$ and dictionary $$P$$ must be updated if needed. The function must not explicity return something (read: must return value None).
-
Write a function path that takes a state $$p$$ of test tubes and a dictionary $$P$$ (dict) with predecessors. The dictionary $$P$$ described the predecessors at a point in time while applying the standard procedure to solve a test tube puzzle and at that moment state $$p$$ has previously been added to the queue. The function must return a list with states that describe the path from the initial state to state $$p$$, as reconstructed from dictionary $$P$$. The function may not modify dictionary $$P$$.
-
Write a function solution that takes three arguments describing a generalized version of the test tube puzzle: i) the initial state $$p$$ of the test tubes, ii) the capacity $$c$$ of the test tubes and iii) a requested volume of liquid $$v \in \mathbb{N}_0$$ (int). The value None must be returned if the puzzle has no solution. Otherwise, the function must return the solution that is obtained from the standard procedure, as a list of states describing the shortest path of successive states.
All these functions may assume that only valid arguments are passed, without having to check this explicitly.
Example
>>> pour((0, 2, 6), (3, 5, 8), 2, 0)
(3, 2, 3)
>>> pour((0, 2, 6), (3, 5, 8), 2, 1)
(0, 5, 3)
>>> pour((3, 2, 3), (3, 5, 8), 1, 0)
>>> pour((3, 2, 3), (3, 5, 8), 2, 2)
>>> next_states((0, 0, 8), (3, 5, 8))
{(0, 5, 3), (3, 0, 5)}
>>> next_states((0, 5, 3), (3, 5, 8))
{(3, 2, 3), (0, 0, 8), (3, 5, 0)}
>>> next_states((3, 0, 5), (3, 5, 8))
{(0, 3, 5), (0, 0, 8), (3, 5, 0)}
>>> queue = [(0, 0, 8)]
>>> predecessor = {(0, 0, 8): None}
>>> step(queue, predecessor, (3, 5, 8))
>>> queue
[(0, 5, 3), (3, 0, 5)]
>>> predecessor
{(0, 0, 8): None, (0, 5, 3): (0, 0, 8), (3, 0, 5): (0, 0, 8)}
>>> step(queue, predecessor, (3, 5, 8))
>>> queue
[(3, 0, 5), (3, 2, 3), (3, 5, 0)]
>>> predecessor
{(0, 0, 8): None, (0, 5, 3): (0, 0, 8), (3, 0, 5): (0, 0, 8), (3, 2, 3): (0, 5, 3), (3, 5, 0): (0, 5, 3)}
>>> path((3, 5, 0), predecessor)
[(0, 0, 8), (0, 5, 3), (3, 5, 0)]
>>> solution((0, 0, 8), (3, 5, 8), 4)
[(0, 0, 8), (0, 5, 3), (3, 2, 3), (0, 2, 6), (2, 0, 6), (2, 5, 1), (3, 4, 1)]
>>> solution((0, 5, 0, 17), (3, 5, 11, 17), 7)
[(0, 5, 0, 17), (0, 0, 5, 17), (0, 5, 5, 12), (0, 0, 10, 12), (0, 5, 10, 7)]
>>> solution((0, 0, 0, 0, 13), (5, 7, 7, 11, 13), 12)
[(0, 0, 0, 0, 13), (0, 0, 0, 11, 2), (5, 0, 0, 6, 2), (0, 0, 0, 6, 7), (5, 0, 0, 1, 7), (0, 0, 0, 1, 12)]