Men kan een benadering van $$\pi$$ berekenen aan de hand van het volgende algoritme :
- beschouw een vierkant met een zijde van lengte 2
- beschouw de ingeschreven cirkel
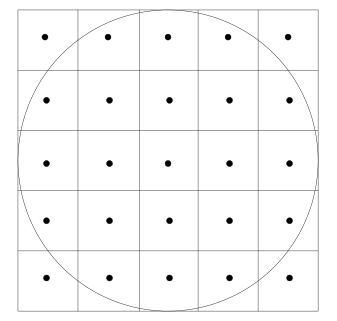
- plaats een raster over het vierkant (zie figuur)
- tel het aantal middelpunten van de rastercellen dat binnen de cirkel ligt
- bereken de benadering voor $$\pi$$ door de oppervlakte van deze cellen als benadering voor de oppervlakte van een cirkel te nemen
pie_vierkant() die, gegeven
het aantal onderverdelingen $$n$$ waarin de zijde het grote vierkant moet opgedeeld worden, een benadering voor $$\pi$$ berekent.
Het totaal aantal vierkantjes is dus $$n^2$$.
 Pi met Vierkantjes/div>
Pi met Vierkantjes/div>
Argumenten
Een geheel getal $$n > 0$$
Resultaat
De gezochte benadering voor $$\pi$$.
Voorbeeld
pie_vierkant(10) = 3.2 pie_vierkant(100) = 3.1440000000000006 pie_vierkant(1000) = 3.141824