Reading through a book from cover to cover, starting with the first page, turning to the next page, and so on, until we reach the last page — that's really old-school. Instead, we treat page numbers as hyperlinks: when we finish page 14, we browse 14 pages further and read through.

In a book with old-fashioned page numbering, we would therefore jump from page 14 to page 28. If a hyperlink passes the last page, we go back to the first page and continue counting from there. So, if a book has 100 pages and we have just read page 74, we count 26 pages until we reach page 100, move on to the first page, continue counting and end up on page 48 (because $$26 + 48 = 74$$). But note that with this way of zap reading: as soon as you start reading the last page (in this case page 100), fun's over, because that hyperlink, by definition, will always point to itself. Since the zap reading trajectory is fixed from start to finish, the only degree of freedom is the total number of pages $$n$$. Then the question arises whether there are any values of $$n$$ that make a book fully zap-readable. That is, no single page remains unread.

As a next step, we move away from old-fashioned page numberings. Instead, we randomly assign each of the page numbers 1, 2, …, $$n$$ to the $$n$$ pages of the book. The page numbers are still considered to be a hyperlinks. For example, after reading the page with number 17, we again move forward 17 pages. But in this case, this doesn't say anything about the number of the page we'll end up with, because that can be any number in between 1 and $$n$$. The question then becomes for which values of $$n$$ and any favorably chosen order of the page numbers: are there any books that can be zap-read completely? As a sneak preview: for a book with 8 pages there are two possible numberings.

Assignment

It has been proven that with old-fashioned page numbering, only books with 1 and 2 pages are zap-readable. For books in which the page numbering is a permutation of the numbers $$1, 2, \ldots, n$$, zap-readable books always have an even number of pages $$n$$ if $$n > 1$$.

For an even number of pages $$n$$, one can make a book zap-readable by assigning the page numbers $$n-1, n - 3, n - 5, \ldots, 1$$ to the pages at positions $$1, 2, \ldots, \frac{n}{2}$$, and by assigning the page numbers $$n, n - 2, n - 4, \ldots, 2$$ to the pages at positions $$\frac{n}{2} + 1, \frac{n}{2} + 2, \ldots, n$$.

If the number of pages $$n$$ is a power of 2 — in other words if $$n = 2^m$$ for any $$m \in \mathbb{N}$$ — there is a second construction method to make the book zap-readable: the first page is assigned page number 1 and every subsequent page you read while zap-reading is assigned the next page number (one higher than the one assigned to the previous page).

Your task:

• Write a function iszapreadable that takes a list containing $$n \in \mathbb{N}$$ page numbers (int). The function must return a Boolean value (bool) that indicates whether a book with this page numbering is zap-readable. That's the case if the page numbers are a permutation of the numbers $$1, 2, \ldots, n$$ and if you get to read all the pages when zap-reading (starting from the first page).

• Write a function zapbook that takes the number of pages $$n \in \mathbb{N}_0$$ (int) of a book. The function must return a list containing a sequence of page numbers (int) that makes the book zap-readable. For $$n = 1$$ or for an even number of pages, the first construction method must be used. However, if $$n$$ is a power of 2, the list of page numbers must be constructed according the second method given above. An empty list must be returned for any odd number of page numbers $$n > 1$$, because in those cases it is not possible to construct a zap-readable book with $$n$$ pages.

Example

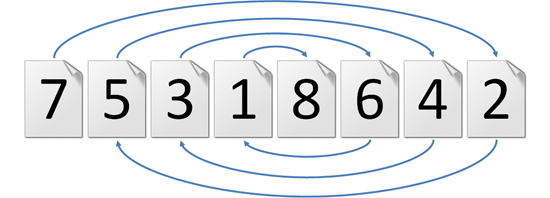
>>> iszapreadable([7, 5, 3, 1, 8, 6, 4, 2])
True
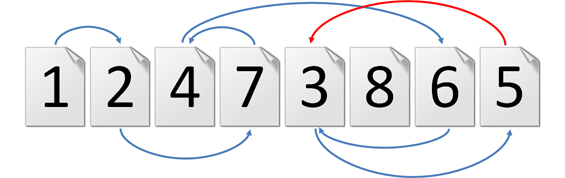
>>> iszapreadable([1, 2, 4, 7, 3, 8, 6, 5])
False
>>> iszapreadable([1, 2, 5, 3, 8, 7, 4, 6])
True
>>> iszapreadable([1, 1, 1, 1, 1, 1, 1, 1])
False

>>> zapbook(6)
[5, 3, 1, 6, 4, 2]
>>> zapbook(7)
[]
>>> zapbook(8)
[1, 2, 5, 3, 8, 7, 4, 6]