Op 15 augustus 1977 ving een telescoop van de Ohio State University een sterk smalbandig radiosignaal op dat afkomstig was uit het sterrenbeeld Boogschutter. Terwijl de antenne dat deel van de hemel aan het afspeuren was, steeg de intensiteit van het signaal plots, hield gedurende 72 seconden aan en viel daarna weer terug. Dit komt overeen met een signaal van niet-aardse en niet-zonnestelselachtige oorsprong, en was voorheen nog nooit in dergelijke mate geobserveerd.

Sterrenkundige Jerry Ehman — die op het moment van de detectie in het observatorium van wacht was — was zo verbaasd over de intensiteitsvariatie van het gelokaliseerd signaal, dat hij onmiddellijk het signaal 6EQUJ5 afdrukte en ernaast in de marge de tekst Wow! bijschreef. Deze commentaar gaf later ook de naam aan het signaal.

Op 15 augustus 1977 ving een telescoop van de Ohio State University een sterk smalbandig radiosignaal op dat afkomstig was uit het sterrenbeeld Boogschutter. Terwijl de antenne dat deel van de hemel aan het afspeuren was, steeg de intensiteit van het signaal plots, hield gedurende 72 seconden aan en viel daarna weer terug. Dit komt overeen met een signaal van niet-aardse en niet-zonnestelselachtige oorsprong, en was voorheen nog nooit in dergelijke mate geobserveerd. Sterrenkundige Jerry Ehman, die op het moment van de detectie in het observatorium van wacht was, was zo verbaasd over de intensiteitsvariatie van het gelokaliseerd signaal dat hij onmiddellijk het signaal 6EQUJ5 afdrukte en ernaast in de marge de tekst Wow! bijschreef. Deze commentaar gaf later ook de naam aan het signaal.

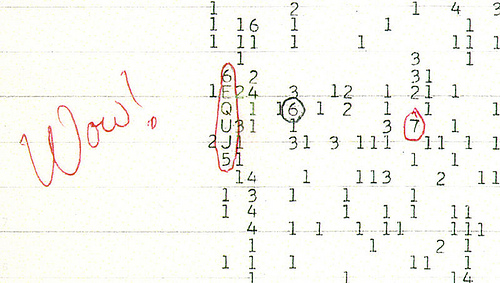
Bijna 40 jaar en meer dan 100 zoektochten later, is nog niemand er in geslaagd om het signaal opnieuw op te pikken. Zonder herhaalde observatie is het onmogelijk om uit te vissen wat Ehman's telescoop die nacht heeft opgepikt, en is het niet meer dan een frustrerende plons in een grote, stille zee.

Opgave

Elke regel van het tekstbestand wow.txt1 bestaat uit een patroon $$p \in \mathcal{P}$$, gevolgd door één enkele spatie en een woord $$w \in \mathcal{W}$$. De verzameling $$\mathcal{P}$$ bevat alle mogelijke signalen die enkel bestaan uit hoofdletters, cijfers en leestekens. De verzameling $$\mathcal{W}$$ bevat alle woorden die enkel bestaan uit kleine letters. Gevraagd wordt:

  1. Bepaal zo kort mogelijke reguliere expressies voor de volgende deelverzamelingen van $$\mathcal{P}$$:

    • $$\mathcal{P}_1 = \{ p \in \mathcal{P}\,|\,$$ alle cijfers komen hoogstens één keer in $$p$$ voor $$\}$$

      voorbeelden: -9----5---D------@--7--6*-------I----3-- $$\in \mathcal{P}_1$$
        -0--9----8@-3-OT---99-}9-[--------2----- $$\not\in \mathcal{P}_1$$

    • $$\mathcal{P}_2 = \{ p \in \mathcal{P}\,|\,$$ $$p$$ bevat een reeks van minstens tien opeenvolgende cijfers en/of hoofdletters $$\}$$

      voorbeelden: 3----08--5-8--4E6PUOCA85HA3-5-3---27---- $$\in \mathcal{P}_2$$
        -U<------T--1--=36-----7------*-72------ $$\not\in \mathcal{P}_2$$

    • $$\mathcal{P}_3 = \{ p \in \mathcal{P}\,|\,$$ $$p$$ bevat een reeks van vier cijfers die drie keer herhaald wordt $$\}$$

      voorbeelden: --04----19259--60-----9259-4---9259--8-- $$\in \mathcal{P}_3$$
        ------698--76-8-----3--3---2-----0-3---9 $$\not\in \mathcal{P}_3$$

    • $$\mathcal{P}_4 = \{ p \in \mathcal{P}\,|\,$$ $$p$$ bevat een alternerende reeks van cijfers en hoofdletters van minstens lengte 9 $$\}$$

      voorbeelden: Q---6------8E8U5C9C3E-6--Y---4----U--2-- $$\in \mathcal{P}_4$$
        -0--9----8@-3-OT---99-}9-[--------2----- $$\not\in \mathcal{P}_4$$

    Geef telkens een Unix commando waarin de reguliere expressie gebruikt wordt door een commando uit de grep familie om enkel de regels van het tekstbestand naar stdout te schrijven waarvan het patroon $$p$$ behoort tot $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$.

  2. Bepaal als volgt de woorden $$w_1\ w_2\ w_3\ w_4$$ van een geheime boodschap:

    • het woord $$w_1$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_1 \cap \mathcal{P}_2$$

    • het woord $$w_2$$ staat op de unieke regel waarvan $$p$$ behoort tot $$ \mathcal{P}_2 \cap \mathcal{P}_3$$

    • het woord $$w_3$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_3  \cap \mathcal{P}_4$$

    • het woord $$w_4$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_4 \cap \mathcal{P}_1$$

    Geef telkens een Unix commando waarin de reguliere expressies voor de verzamelingen $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$ gebruikt worden door commando's uit de grep familie om het woord $$w_j\ (j = 1, 2, 3, 4)$$ op te zoeken in het tekstbestand en uit te schrijven naar stdout. Hierbij is het niet toegelaten om het woord $$w_j$$ letterlijk uit te schrijven (bv. echo $$w_j$$).