As one of the last steps of genetic recombination two homologous chromosomes can exchange genetic material during meiosis in a process that is referred to as synapsis. Because of this chromosomal crossover, recombined chromosomes arise. Crossover usually occurs when corresponding regions of corresponding chromosomes break and thereafter attach back to the other chromosome.

A theoretical description of crossover was introduced by Thomas Hunt Morgan, who was inspired by the work of the Belgian Professor Frans Alfons Janssens of the University of Leuven. The latter had already described his chiasmatype theory in 1909.

Assignment

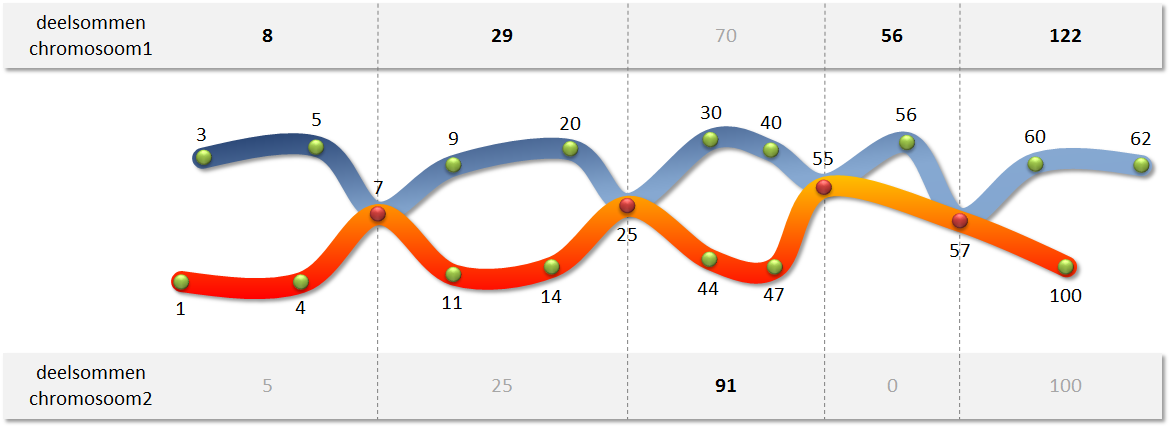
In this assignment, we represent a chromosome as a list or a tuple of strictly increasing integers (each number is larger than the previous number). The points where two chromosomes can break open - and where a crossover can occur - are indicated by the common numbers in the two corresponding lists or tuples. This is illustrated in the figure below, where crossover can occur where the two chromosomes meet.

The chromosomes can be navigated through the following way:

1. As a starting point the beginning (the left side) of one of the two chromosomes can be selected.

2. Stepping forward (to the right) is possible from any point.

3. At a crossover point, you have the choice to continue on the same chromosome, or switch to the other chromosome.

Asked:

• Write a function crossoverpoints to which two chromosomes must be passed. The function should return how many crossover points there are between these chromosomes.

• Write a function maximumSum to which two chromosomes must be passed. The function should determine the maximum sum of all paths that can be followed in the manner described above. In the example above, the maximum sum of 450 is achieved by going through the following path:

3 + 5 + 7 + 9 + 20 + 25 + 44 + 47 + 55 + 56 + 57 + 60 + 62

The maximum sum is found by determining the maximum partial sums of the fragments before the first crossover point, between successive crossover points, and after the last crossover point. Note that it is possible that two partial sums are equal, if the end points themselves are crossover points, or if two crossover points immediately follow each other without intermediate points.

Algorithm

In order to find the crossover points, you can use the fact that the numbers in the two data frames are strictly increasing. In that way, you can go through the lists simultaneously from left to right, while you keep track of your position for each list separately. Always move one step ahead in the list from where at the current position is the smallest number. If you find a similar number on the current position in both lists, then you have found a crossover point. While running through both lists, you can also determine the partial sums before, between, and after the crossover points.

Example

>>> chromosome1 = [3, 5, 7, 9, 20, 25, 30, 40, 55, 56, 57, 60, 62]
>>> chromosome2 = [1, 4, 7, 11, 14, 25, 44, 47, 55, 57, 100]
>>> crossoverpoints(chromosome1, chromosome2)
4
>>> maximumSum(chromosome1, chromosome2)
450

>>> chromosome1 = [-5, 100, 1000, 1005]
>>> chromosoom2 = [-12, 1000, 1001]
>>> crossoverpoints(chromosome1, chromosome2)
1
>>> maximumSum(chromosome1, chromosome2)
2100

Resources

• Morgan TH (1916). A Critique of the Theory of Evolution. Princeton, NJ, Princeton University Press. ¹