A telephone company is putting down cell towers to further improve their mobile phone network. It wants to place the towers in such a way that the average signal strength over a range of reception points is as large as possible.

If a signal is sent from a tower with co-ordinates $$(x_z, y_z)$$, we assume in this assignment that the signal strength $$s \in [0, 1]$$ in a reception point with co-ordinates $$(x_o, y_o)$$ only depends on the distance $$r$$ between the reception point and the towers, and on a parameter $$\alpha$$ that indicates the power of the towers. The distance is given by \[r = \sqrt{(x_o - x_z)^2 + (y_o - y_z)^2}\] We will also assume that all towers have the same amount of power. Each model can therefor be described by a signal function $$f(r, \alpha)$$. This function takes a value between 0 and 1 for a point on a given distance to the tower, which indicates the signal power level.

Various functions expressing the signal strength $$s$$ of the tower's signal as a function of the distance $$r$$ to the tower, with the power of the towers being $$\alpha = 2$$.

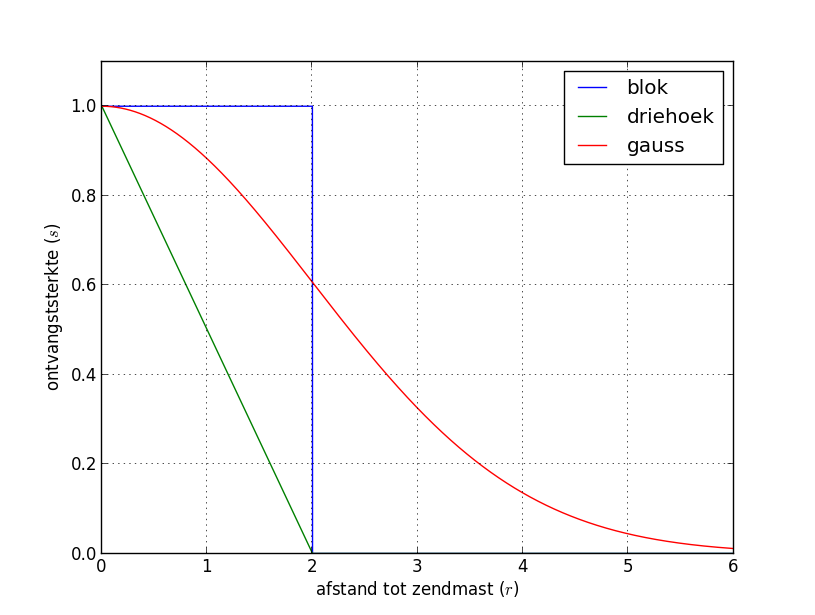
The graph above shows the course of the signal strength $$s$$ for a number of models, as a function of the distance $$r$$ to the tower:

block strength (block): all points within a radius $$\alpha$$ (including the points on the edge) have signal power level 1, and the external points have signal power level 0
triangular strength (triangle): the signal strength decreases linearly from 1 at the tower to 0 for points at a distance $$\alpha$$ to the tower; points at a distance larger than $$\alpha$$ to the tower also have signal power level 0
strength according to Gaussian function (gauss): the signal strength is provided by $$e^{\frac{-r^2}{2\alpha^2}}$$

If a reception point receives signals from multiple towers, then the signal strength at that point equals the maximum signal strength of the signals from the individual towers.

Preparation

In Python functions are themselves objects, so you can use them like any other objects. In particular, you can assign functions to variables or pass them as an argument to other functions. For example, consider the following three functions.

def repeat(value, function, number):
    for i in range(number):
        value = function(value)
    return value

def increase(value):
    return value + 1

def decrease(value):
    return value - 1

Below is an example of how these functions can be used. Check how Python reacts when you run the following sequence of instructions within an interactive Python session where you first ensure that the above functions were defined. Make sure that you understand why you get a certain value, and what actually happens in the interactive session before proceeding with the actual task.

>>> increase(5)
>>> decrease(101)
>>> repeat(5, increase, 3)
>>> repeat(5, decrease, 3)
>>> repeat(5, decrease, increase(3))

Assignment

Write three functions block, triangle and gauss, that constitute an implementation of the corresponding signal functions described in the introduction of this assignment. Each function should be passed two arguments: a distance $$r$$ between a tower and a reception point, and the strength $$\alpha$$ of the tower. Each function should return the corresponding signal strength as a real number between 0 and 1.
Write a function receptionquality that returns the average signal strength, measured over a series of reception points. The function has two obligatory parameters towers and receptionpoints to which respectively a list of co-ordinates of the towers and a list of co-ordinates of reception points must be passed. Each co-ordinate is then represented as a tuple $$(x, y)$$. The function also has two optional parameters. A parameter alpha, indicating the strength $$\alpha$$ of the towers (default value 5.0), and a parameter signalfunction to which a signal function $$f(r, \alpha)$$ can be passed that models the type of the towers (towers usually have a block strength.)

Example

>>> block(1.0, 2.0)
1.0
>>> triangle(1.0, 2.0)
0.5
>>> gauss(1.0, 2.0)
0.8824969025845955

>>> towers = [(0.0, 0.0), (5.0, 5.0), (3.0, 4.0)]
>>> receptionpoints = [(1.2, 4.3), (2.8, 3.3), (3.2, 0.7), (-1.0, -1.0), (10.0, 0.0)]
>>> receptionquality(towers, receptionpoints)
0.8
>>> receptionquality(towers, receptionpoints, alpha=3.0)
0.6
>>> receptionquality(towers, receptionpoints, signalfunction=triangle)
0.5102911527511019
>>> receptionquality(towers, receptionpoints, signalfunction=gauss)
0.8121116675748477

Below is a map that shows the situation for the first case in the above doctest. After you have submitted your solution, you can also view some maps to assist you in debugging. By clicking on the reception points of the towers you will see additional information.