Given a rectangular grid of \(n\) rows and \(m\) columns of connections of equal length. However, certain crossings are inaccessible. You have to determine the number of distinct shortest routes from the corner \((0,0)\) to the corner \((n-1,m-1)\).

E.g., the grid below with 4 rows and 7 columns has 18 distinct shortest routes from \(H=(0,0)\) to \(P=(3,6)\).

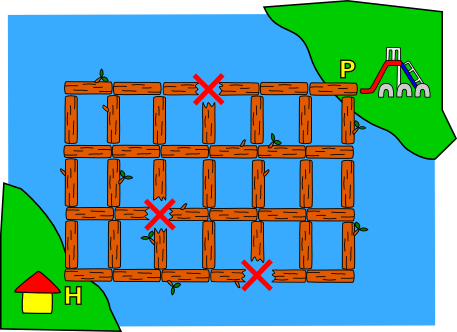
Assignment

Write a Python function countNumberOfShortestRoutes that takes as parameters the number \(n\) of rows and the number \(m\) of columns of the grid, as well as a list of coordinates of blocked positions. The function should return the number of distinct shortest routes from \((0,0)\) to \((n-1,m-1)\).

Example

>>> countNumberOfShortestRoutes(4,7,[(0,4),(1,2),(3,3)])
18
>>> countNumberOfShortestRoutes(5,8,[(1,1),(3,4),(4,6),(2,7)])
27
>>> countNumberOfShortestRoutes(10,15,[(2,3),(4,5),(6,9),(9,10),(7,8),(2,6),(7,3),(9,13),(1,2)])
32464
>>> countNumberOfShortestRoutes(5,5,[(4,0),(3,1),(2,2),(1,3),(0,4)])
0
>>> countNumberOfShortestRoutes(10,15,[(2,2),(6,4),(4,7),(8,10)])
242774
>>> countNumberOfShortestRoutes(15,20,[(3,4),(6,5),(1,5),(8,2),(12,19),(14,7),(13,4)])
266273165
>>> countNumberOfShortestRoutes(10,15,[])
817190