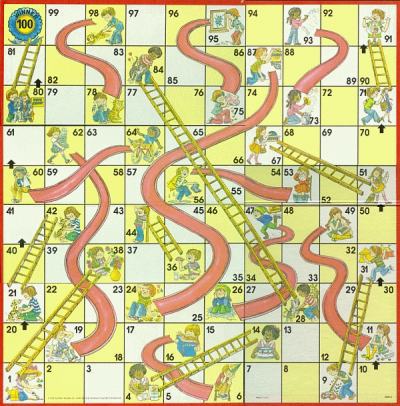
Chutes and Ladders is a classic board game for children. It is played between two or more players on a board having 100 numbered spaces. The spaces are numbered 1 to 100 and are arranged in a square $$10 \times 10$$ grid with 10 rows and 10 columns. A number of chutes and ladders are pictured on the board, each connecting two specific spaces on the board. A chute connects a space with another space that has a lower number. A ladder connects a space with another space that has a higher number.
All players have their tokens initially off-the-board at what is effectively space zero. They move their tokens alternately along the numbered spaces on the board according to the roll of a die. Tokens that land on the top end of a chute are demoted to the space at the bottom end of the chute, and tokens that land on the bottom end of a ladder are promoted to the space at the top end of the ladder. Space 100 must be reached by exact roll of the die. If the roll of the die would take the token past space 100, the token remains where it is and play passes to the next player. The winner of the game is the first token to reach space 100.
Assignment
In this assignment we represent the configuration of chutes and ladders on the game board as dictionaries, with numbers of spaces on top of a chute or at the bottom of a ladder used as keys. Their associated values are the corresponding numbers of the spaces at the other end of the chute or the ladder. A roll of a die is represented by an integer that indicates the number of pips on top of the die. Your task:
-
Write a function merge that takes two arguments that respectively represent the configuration of the chutes and the configuration of the ladders on the game board. The function must return a new dictionary whose keys are the numbers of the spaces on the game board at the top of a chute or at the bottom of a ladder. Each key must be mapped onto an integer that indicates how many spaces the token moves forward (in case of a ladder) or backward (in case of a chute) from the space numbered with the key.
-
Use the function merge to write a function spaces that takes three arguments: i) a sequence (a list or a tuple) of rolls of a die, ii) the configuration of the chutes on the game board and iii) the configuration of the ladders on the game board. The function must return a list containing the number of the spaces the player's token finishes on after each turn, if the player rolls the die in the given sequence. We assume that the token is initially off-the-board at what is effectively space zero.
The following rules must be followed when configuring chutes and ladders on the game board:
-
a space can not simultaneously be the starting point of a chute and a ladder
-
the displacement of a chute must always end in a space with a lower number
-
the displacement of a ladder must always end in a space with a higher number
If the configuration of the chutes and ladders passed to the functions merge en spaces does not meet these criteria, the functions must raise an AssertionError with the message invalid configuration. Note that it is allowed that a chute or ladder ends in a space where another chute or ladder starts. As a consequence, it might well be that a players' token has to follow multiple chutes and/or ladders in a single turn.
Example
>>> chutes = {98: 78, 95: 75, 93: 73, 87: 24, 64: 60, 62: 19, 56: 53, 49: 11, 47: 26, 16: 6}
>>> ladders = {1: 38, 4: 14, 9: 31, 21: 42, 28: 84, 36: 44, 51: 67, 71: 91, 80: 100}
>>> merge(chutes, ladders)
{64: -4, 1: 37, 4: 10, 71: 20, 9: 22, 16: -10, 21: 21, 87: -63, 28: 56, 93: -20, 95: -20, 80: 20, 98: -20, 36: 8, 47: -21, 49: -38, 51: 16, 56: -3, 62: -43}
>>> chutes
{98: 78, 95: 75, 93: 73, 87: 24, 64: 60, 62: 19, 56: 53, 49: 11, 47: 26, 16: 6}
>>> ladders
{1: 38, 4: 14, 9: 31, 21: 42, 28: 84, 36: 44, 51: 67, 71: 91, 80: 100}
>>> merge({23: 32}, {44: 44})
Traceback (most recent call last):
AssertionError: invalid configuration
>>> spaces([1, 4, 5], chutes, ladders)
[38, 42, 26]
>>> spaces([2, 4, 1, 4, 5, 5, 4, 2], chutes, ladders)
[2, 6, 7, 11, 6, 11, 15, 17]
>>> spaces([5] * 16, chutes, ladders)
[5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 100]
>>> spaces([6] * 14, chutes, ladders)
[6, 12, 18, 24, 30, 44, 50, 53, 59, 65, 91, 97, 97, 97]
>>> spaces([4, 2, 5, 6], {23: 32}, {44: 44})
Traceback (most recent call last):
AssertionError: invalid configuration
Epilogue
Snakes and Ladders originated in India as part of a family of dice board games, that included Gyan Chauper1 and Pachisi2 (present-day Ludo3 and Parcheesi4). In the original version of the game — named Moksha Patam — chutes were represented by snakes. It was associated with traditional Hindu philosophy, where ladders represented virtues such as generosity, faith and humility, while snakes represented virtues such as lust, anger, murder and theft. The morality lesson of the game was that a person can attain salvation (Moksha) through doing good, whereas by doing evil one will inherit rebirth to lower forms of life. The number of ladders was less than the number of snakes as a reminder that a path of good is much more difficult to tread than a path of sins. Presumably, reaching the last square (number 100) represented the attainment of Moksha (spiritual liberation).

There are several interesting questions that can be asked about the Snakes and Ladders game. First, what is the minimum number of rolls required to reach space 100. Second, for a single player, what is the average number of rolls required to reach space 100. And third, for $$k \geq 2$$ players, what is the average number of rolls until one of the players reaches space 100 and wins the game. S.C. Althoen, L. King and K. Schilling studied these and other questions in their paper "How long is a game of snakes and ladders?".