Due to a catastrophic admin blunder, Easter Bunny only learns in the early hours of of Easter Sunday that he must quickly collect another 25 Easter eggs that are scattered across a grid-like region.

Possible start configuration of an Easter Egg puzzle, with 25 Easter eggs and Easter Bunny in the center of a $$7 \times 7$$ grid.

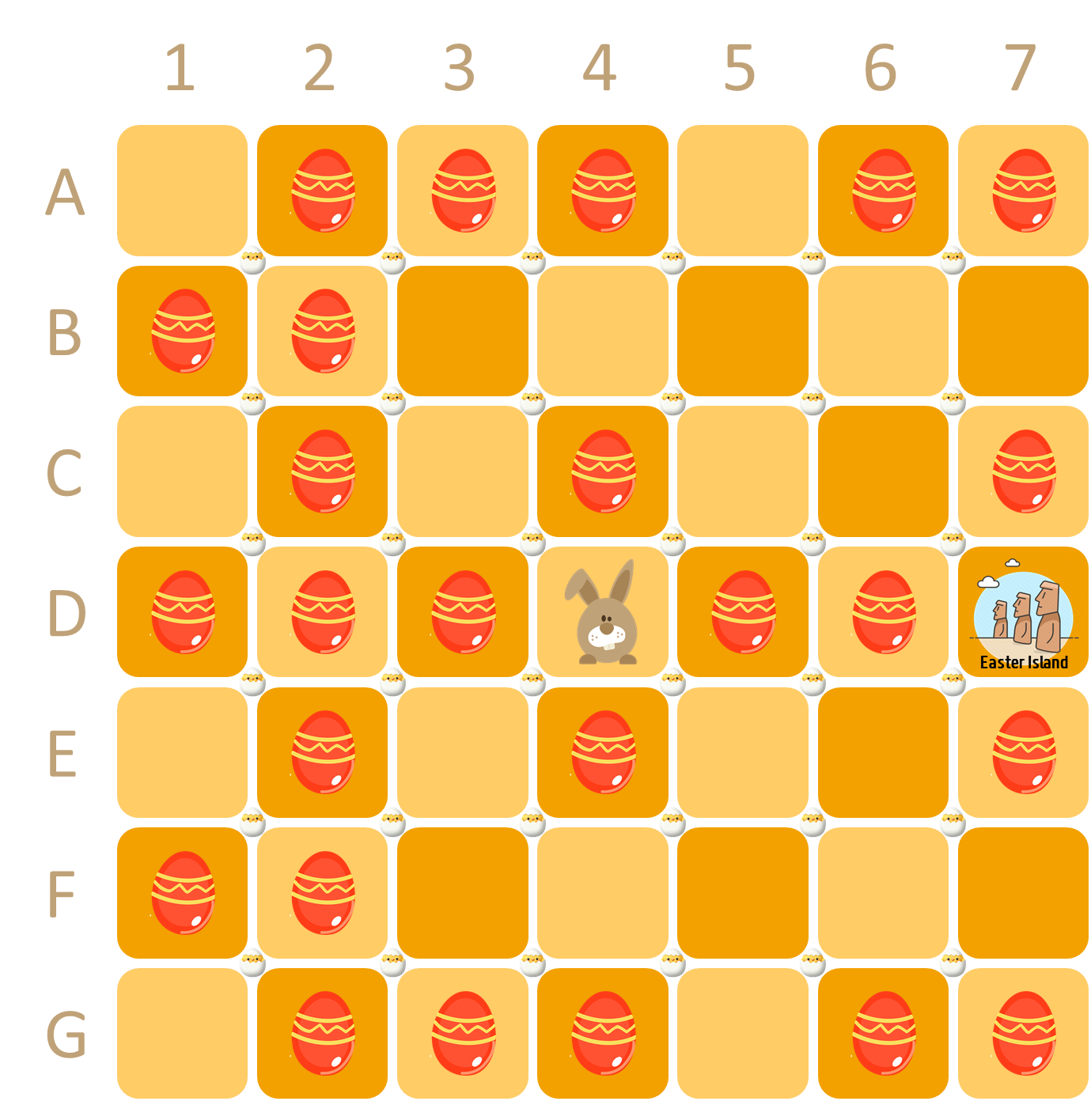
Easter Bunny initially stands on square D4. On each move, he jumps to a different position in the grid, either like a chess knight (one step horizontally or vertically and two steps in the other direction) or any number of squares eastwards (to the right) of his current position. In other words, from his starting position D4 (left grid below) Easter Bunny could move next to any of the following eleven squares: B3, B5, C2, C6, E2, E6, F3, F5, D5, D6 or D7. If Easter Bunny were stood on square A6 (right grid below), he could move next to B4, C5, C7 or A7.

Possible moves if Easter Bunny is at position D4. Green arrows indicate possible moves like a chess knight. Blue arrows indicate possible moves eastwards (to the right).

Possible moves if Easter Bunny is at position D6. Green arrows indicate possible moves like a chess knight. Blue arrows indicate possible moves eastwards (to the right).

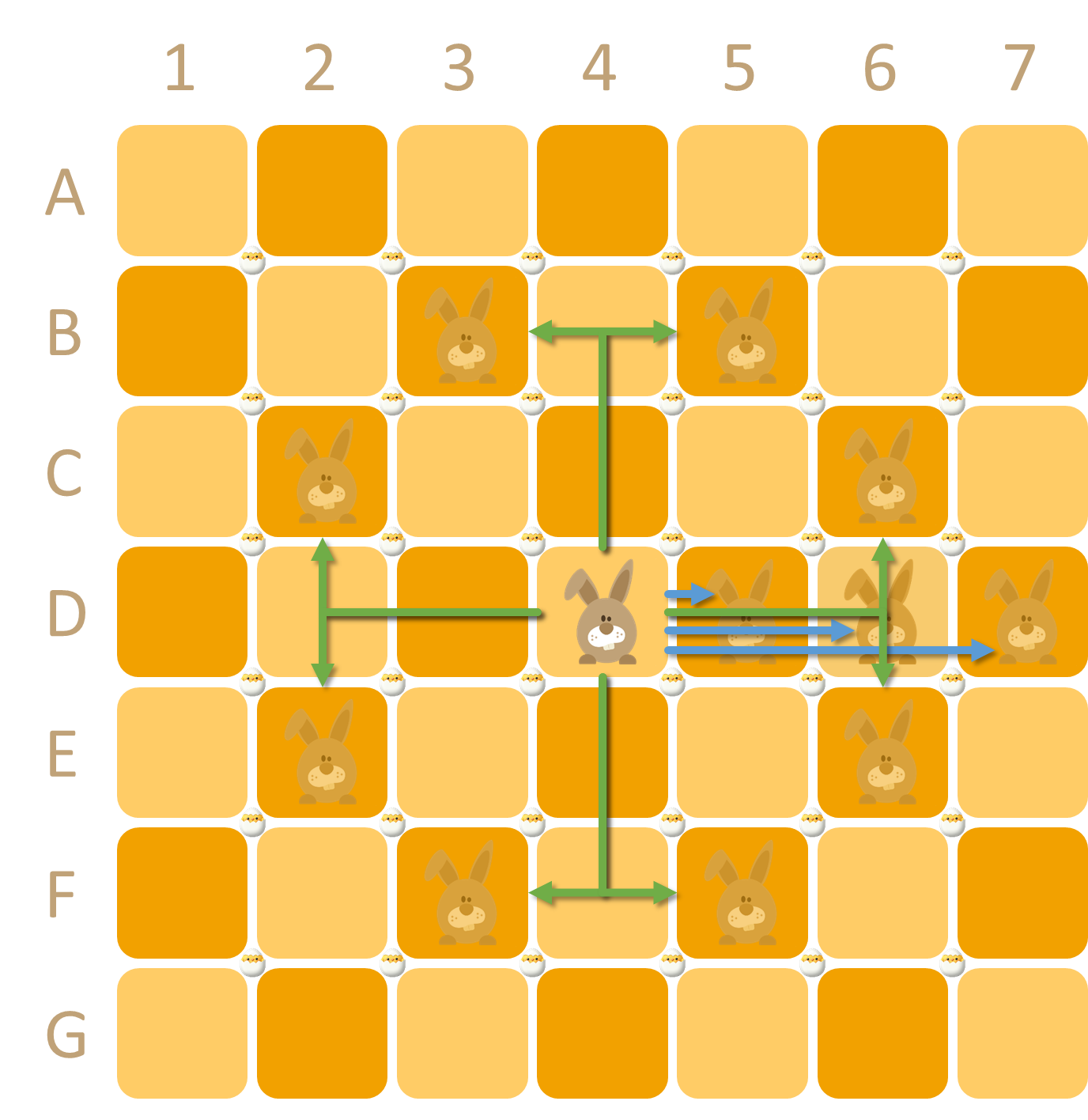
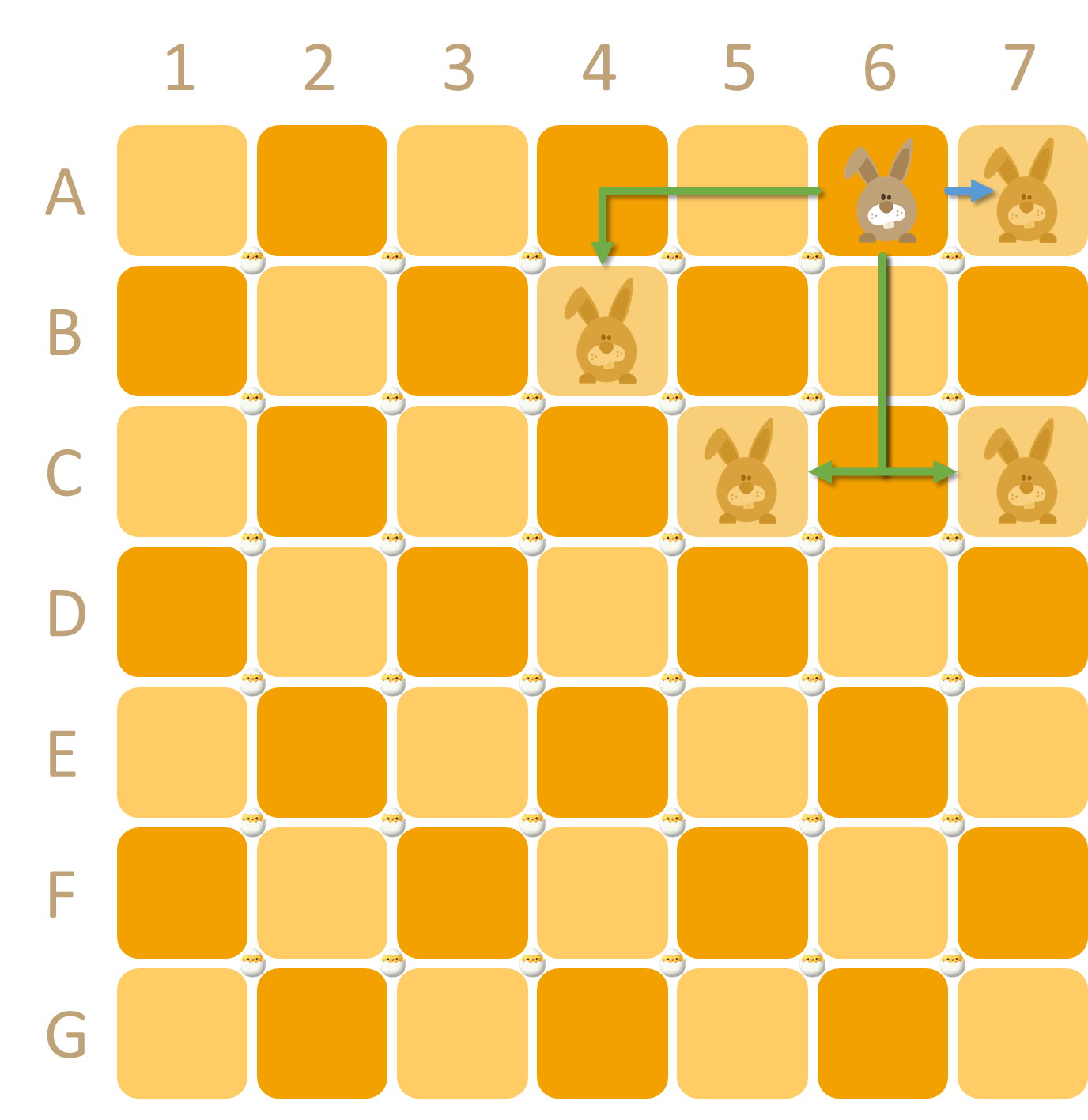
Naturally, Easter Bunny must land directly on a square to visit it — for instance, if he were to jump from D4 to D6 with his first move, he could pick up the egg on position D6, but not the egg on position D5. As a consequence, Easter Bunny can pick up at most one egg on each move.

What is the smallest number of moves required for Easter Bunny to pick up all 25 eggs and then return home to Easter Island¹ (position D7) — and what route should he take?

Assignment

The introduction describes an Easter Egg puzzle that in general works with a rectangular $$m \times n$$ grid with $$m$$ rows ($$2 \leq m \leq 26$$) and $$n$$ columns ($$2 \leq n \leq 26$$). The rows of the grid are labeled from top to bottom with successive uppercase letters of the alphabet. The columns of the grid are numbered from left to right, starting at 1. A position in the grid can therefore be represented as a string (str) consisting of an uppercase letter that indicates the row, followed by a number that indicates the column.

Define a class EasterEgg to simulate the process of solving Easter Egg puzzles. Four arguments must be passed when creating a new puzzle (EasterEgg): i) the number of rows $$m$$ of the grid, ii) the number of columns $$n$$ of the grid, iii) the starting position of Easter Bunny, and iv) the location (str) of a text file containing the initial positions of the Easter eggs (one position per line). The implementation of the class may assume that the arguments describe a valid starting configuration, without the need to check this explicitly: Easter Bunny and all eggs are positioned within the grid boundaries, and there's no egg at the starting position of Easter Bunny.

If a puzzle (EasterEgg) is passed to the built-in function str, it must return a string representation (str) of the grid in which each row is a separate line, empty squares are represented by a hash symbol (#), squares with an egg are represented by an uppercase letter O and the square where Easter Bunny stands is represented by uppercase letter X.

In addition, a puzzle (EasterEgg) must support at least the following methods:

A method bunny that takes no arguments and returns the position (str) where Easter Bunny currently stands.
A method eggs that takes no arguments and returns a set with the positions (str) of all remaining eggs.
A method possible_moves that takes no arguments and returns a set with all positions (str) Easter Bunny could move next from its current position.
A method move that takes a position $$p$$ (str). If Easter Bunny cannot move next to position $$p$$ from its current position, Easter Bunny must keep its current position and the method must raise an AssertionError with the message invalid move. Otherwise, Easter Bunny must move to position $$p$$ and collect any egg at that position (such that the egg disappears from the grid), and the method must return a reference to the object on which it was called.
A method isempty that takes no arguments and returns a Boolean value (bool) that indicates whether there are no more eggs on the grid.

Example

In the following interactive session, we assume the current directory contains the text file eggs.txt².

        >>> puzzle = EasterEgg(7, 7, 'D4', 'eggs.txt3')
>>> puzzle.bunny()
'D4'
>>> puzzle.eggs() # doctest: +SKIP
{'A2', 'A3', 'A4', 'A6', 'A7', 'B1', 'B2', 'C2', 'C4', 'C7', 'D1', 'D2', 'D3', 'D5', 'D6', 'E2', 'E4', 'E7', 'F1', 'F2', 'G2', 'G3', 'G4', 'G6', 'G7'}
>>> print(puzzle)
#OOO#OO
OO#####
#O#O##O
OOOXOO#
#O#O##O
OO#####
#OOO#OO
>>> puzzle.isempty()
False
>>> puzzle.possible_moves() # doctest: +SKIP
{'B3', 'B5', 'C2', 'C6', 'D5', 'D6', 'D7', 'E2', 'E6', 'F3', 'F5'}
>>> print(puzzle.move('E2'))
#OOO#OO
OO#####
#O#O##O
OOO#OO#
#X#O##O
OO#####
#OOO#OO
>>> puzzle.bunny()
'E2'
>>> puzzle.eggs() # doctest: +SKIP
{'A2', 'A3', 'A4', 'A6', 'A7', 'B1', 'B2', 'C2', 'C4', 'C7', 'D1', 'D2', 'D3', 'D5', 'D6', 'E4', 'E7', 'F1', 'F2', 'G2', 'G3', 'G4', 'G6', 'G7'}
>>> puzzle.isempty()
False
>>> puzzle.possible_moves() # doctest: +SKIP
{'C1', 'C3', 'D4', 'E3', 'E4', 'E5', 'E6', 'E7', 'F4', 'G1', 'G3'}
>>> puzzle.move('B3')
Traceback (most recent call last):
AssertionError: invalid move
>>> puzzle.move('B2')
Traceback (most recent call last):
AssertionError: invalid move
>>> print(puzzle.move('G3').move('F1').move('E3').move('G2').move('G4'))
#OOO#OO
OO#####
#O#O##O
OOO#OO#
###O##O
#O#####
###X#OO
>>> puzzle.possible_moves() # doctest: +SKIP
{'E3', 'E5', 'F2', 'F6', 'G5', 'G6', 'G7'}
>>> print(puzzle.move('F2').move('E4').move('D2').move('B1').move('A3'))
#OXO#OO
#O#####
#O#O##O
O#O#OO#
######O
#######
#####OO
>>> print(puzzle.move('C2').move('C4').move('B2').move('D1').move('D3'))
#O#O#OO
#######
######O
##X#OO#
######O
#######
#####OO
>>> print(puzzle.move('B4').move('A2').move('A4').move('A6').move('A7'))
######X
#######
######O
####OO#
######O
#######
#####OO
>>> print(puzzle.move('C6').move('C7').move('D5').move('E7').move('G6'))
#######
#######
#######
#####O#
#######
#######
#####XO
>>> print(puzzle.move('G7').move('F5').move('D6').move('D7'))
#######
#######
#######
######X
#######
#######
#######
>>> puzzle.isempty()
True