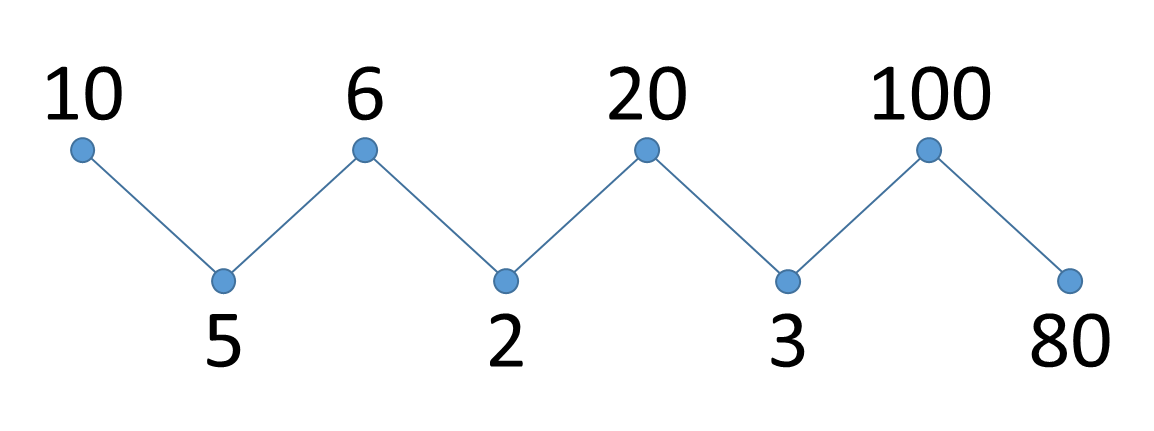
A zigzag sorted sequence of integers $$a_0, a_1, a_2, a_3, a_4, \ldots$$ is a sequence where \[ a_0 \geq a_1 \leq a_2 \geq a_3 \leq a_4 \geq \ldots \] In other words, the sequence alternates between larger and smaller integers: the first is larger than or equal to the second, the second is smaller than or equal to the third, the third is larger than or equal to the fourth, and so on. Here's an example of such a zigzag sorted sequence:

Example of a zigzag sorted sequence of integers.

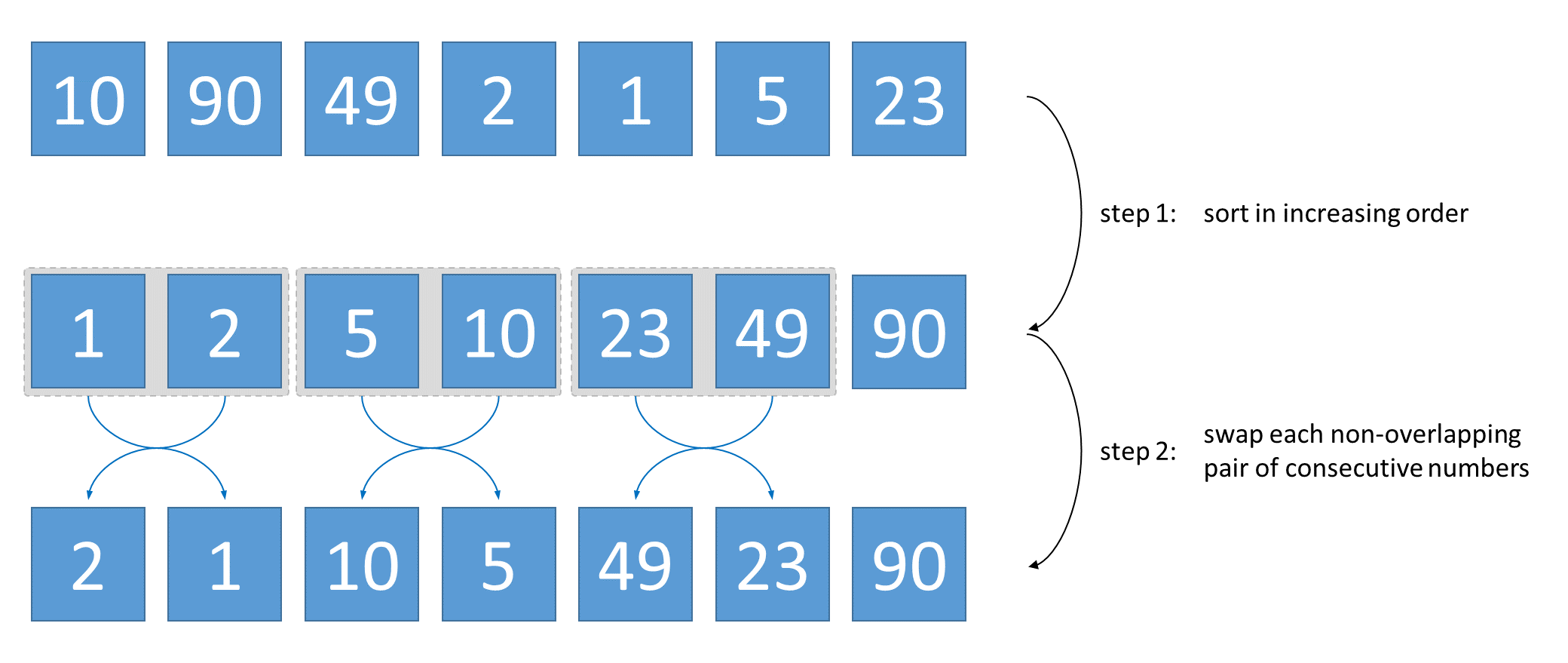
Given an unsorted sequence of integers, a simple way to rearrange the integers into a zigzag sorted sequence is to use sorting. First sort the integers in the sequence in increasing order, then swap each non-overlapping pair of adjacent integers. For example, let the original sequence be [10, 90, 49, 2, 1, 5, 23]. After sorting, we get [1, 2, 5, 10, 23, 49, 90]. After swapping adjacent elements, we get [2, 1, 10, 5, 49, 23, 90].

Slow method to zigzag sort a given sequence of integers.

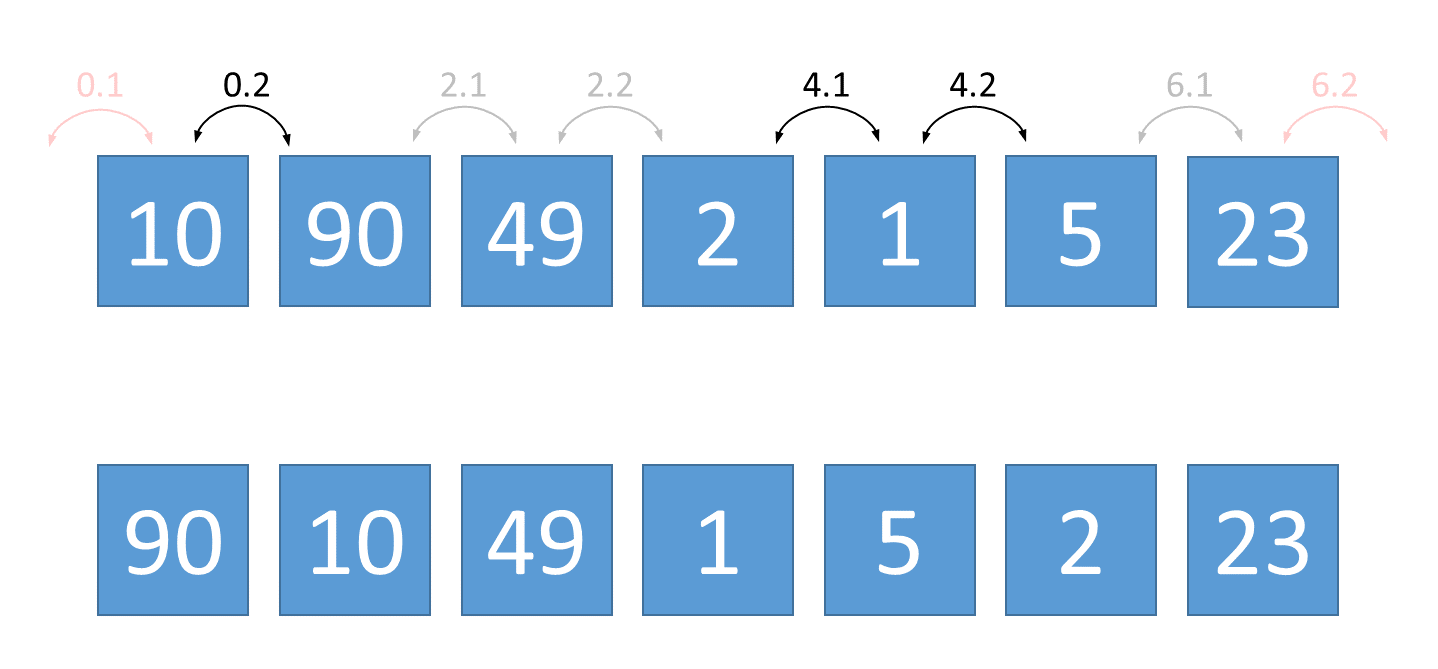
However, there's a faster way to zigzag sort a given sequence of integers that only requires a single traversal over the elements of the sequence. The idea is based on the fact that if we make sure that all even-positioned elements (at indices 0, 2, 4, …) are greater than or equal to their adjacent odd-positioned elements, we do no longer need to worry about the odd-positioned elements. All it requires is to traverse the even positions from left to right, and on each position execute the following two steps one after the other:

if the current element at the even position is less than the element on the previous odd position (if that position exists), swap both elements
if the current element at the even position is less than the element on the next odd position (if that position exists), swap both elements

If we apply this method to the above example, we get

Fast method to zigzag sort a given sequence of integers.

Assignment

Write a function iszigzag that takes a sequence (list or a tuple) of integers (int). The function must return a Boolean value (bool) that indicates whether the given sequence of integers is zigzag sorted.
Write a function zigzag_slow that takes a list (list) of integers (int). The function must zigzag sort the given list of integers using the slow method described above. The function must not return a value (read: return the value None), but must modify the given list in place.
Write a function zigzag_fast that takes a list (list) of integers (int). The function must zigzag sort the given list of integers using the fast method described above. The function must not return a value (read: return the value None), but must modify the given list in place.

Example

        >>> iszigzag([10, 5, 6, 3, 2, 20, 100, 80])
False
>>> iszigzag((10, 5, 6, 2, 20, 3, 100, 80))
True
>>> iszigzag([20, 5, 10, 2, 80, 6, 100, 3])
True

>>> seq = [10, 90, 49, 2, 1, 5, 23]
>>> zigzag_slow(seq)
>>> seq
[2, 1, 10, 5, 49, 23, 90]

>>> seq = [10, 90, 49, 2, 1, 5, 23]
>>> zigzag_fast(seq)
>>> seq
[90, 10, 49, 1, 5, 2, 23]