SMILES¹ of voluit simplified molecular-input line-entry specification is een specificatie waarmee de structuur van chemische moleculen op eenduidige wijze kan genoteerd worden als een ASCII tekenreeks. De meeste chemische tekenprogramma's kunnen SMILES-notatie omzetten naar een tweedimensionale tekening of een driedimensionaal model van het molecuul. Bovendien laat SMILES ook toe om moleculen te indexeren en op te zoeken in een databank.

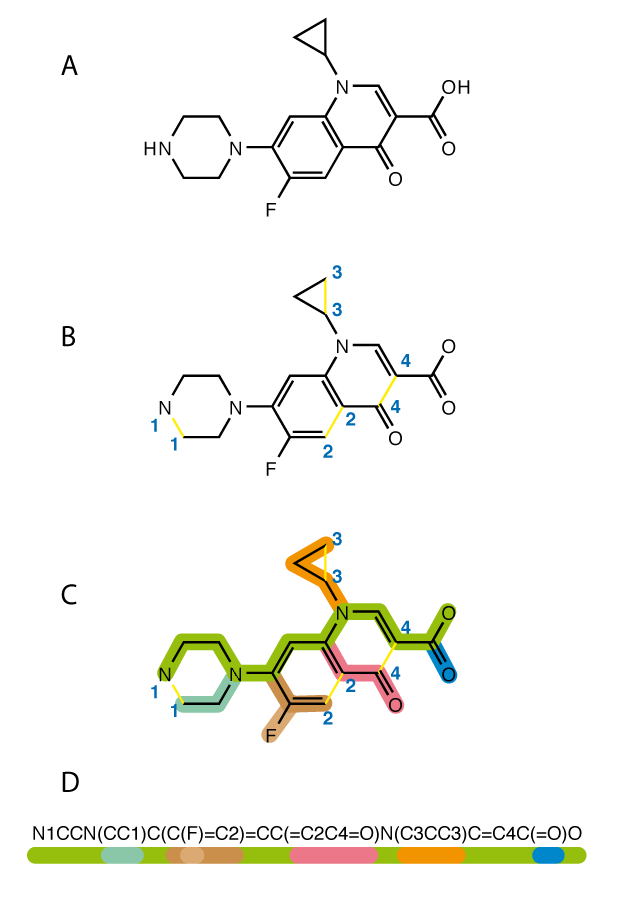
In SMILES wordt een molecuul herleid tot een boomstructuur, waaruit de notatie verkregen wordt door de labels van de knopen in de boom op te sommen zoals bij diepte-eerst zoeken².

Een label in de boom is de symbolische naam voor een chemische element tussen vierkante haakjes. Het label van goud is bijvoorbeeld [Au]. De vierkante haakjes mogen weggelaten worden voor de elementen B, C, N, O, F, P, S, Cl, Br en I. Alle andere elementen moeten tussen vierkante haakjes genoteerd worden. Als de vierkante haakjes weggelaten worden, dan wordt ook impliciet het juiste aantal waterstofatomen (H) verondersteld. Zo kan water³ (H₂O) eenvoudigweg genoteerd worden als O. Op dezelfde manier kan methaan⁴ (CH₄) genoteerd worden als [C]([H])([H])([H])[H] of als het kortere C.

Vertakkingen in de boom worden genoteerd met ronde haakjes, waarbij opeenvolgende vertakkingen genoteerd worden met geneste ronde haakjes. Zo kan L-alanine⁵ bijvoorbeeld genoteerd worden als N[C@H](C(=O)O)C.

Een geladen atoom wordt weergegeven door een aantal keer - (negatieve lading) of + (positieve lading) achter het label te plaatsen, of door één keer - of + en dan een getal, met het geheel tussen vierkante haakjes. Zo kan het hydroxide-anion⁶ bijvoorbeeld genoteerd worden als [OH-] of als [OH-1].

Een molecuul kan één of meer ringstructuren bevatten, die verbroken worden om tot een boomstructuur te komen. Op de plaatsen waar ringen verbroken worden, worden de labels in de boom uitgebreid met een getal. Tussen dezelfde getallen is er een verbinding in het molecuul. Zo kan cyclohexaan⁷ bijvoorbeeld genoteerd worden als C1CCCCC1.

Tussen twee atomen zijn verschillende soorten chemische bindingen mogelijk, die ook in de SMILES-notatie voorgesteld worden. Een enkelvoudige binding wordt niet expliciet voorgesteld, een dubbele binding wordt voorgesteld met een gelijkteken (=) en een drievoudige binding met een hekje (#). Zo wordt koolstofdioxide⁸ bijvoorbeeld voorgesteld als O=C=O en waterstofcyanide⁹ als C#N. Tussen aromatische atomen worden impliciet aromatische bindingen verondersteld, maar ze kunnen ook expliciet voorgesteld worden door een dubbelpunt (:). Eén enkele binding tussen twee aromatische atomen kan ook expliciet aangegeven worden (zoals in bifenyl¹⁰: c1ccccc1-c2ccccc2, hoewel dit niet de meest gebruikelijke notatie is voor bifenyl).

Opgave

Elke regel van het tekstbestand smiles.txt¹¹ bestaat uit een patroon $$p \in \mathcal{P}$$, gevolgd door één spatie en een woord $$w \in \mathcal{W}$$. De verzameling $$\mathcal{P}$$ bestaat uit alle mogelijke SMILES-notaties. Daarbij moet je enkel weten dat een SMILES-notatie bestaat uit een reeks letters (zowel hoofdletters als kleine letters), cijfers en leestekens. Een SMILES-notatie bevat nooit witruimtekarakters zoals spaties, tabs en newlines. De verzameling $$\mathcal{W}$$ bevat alle woorden die enkel uit kleine letters bestaan. Gevraagd wordt:

1. Bepaal zo kort mogelijke reguliere expressies voor de volgende deelverzamelingen van $$\mathcal{P}$$:

   • $$\mathcal{P}_1 = \{\,p \in \mathcal{P}\,|\,p\ $$bevat geen geneste ronde haakjes$$\,\}$$

     voorbeeld:	[O-][N+]([O-])=O.CC1=C(CCO)SC=[N+]1CC1=CN=C(C)N=C1N $$\in \mathcal{P}_1$$
     	Cc1ccc(S(=O)(=O)N2C3CCCCC3O[C@H]2CC(=O)c2cccs2)cc1 $$\not \in \mathcal{P}_1$$

   • $$\mathcal{P}_2 = \{\,p \in \mathcal{P}\,|\,p\ $$bevat een reeks van 8 of meer opeenvolgende cijfers als we alle leestekens$$^{(*)}$$ negeren$$\,\}$$

     (*) alle tekens die geen letter of cijfer zijn
     

     voorbeeld:	1S/C6H10N2O/c1-6(2-5(6)9)4(8)3-7/h4-5,9H,2,8H2,1H3 $$\in \mathcal{P}_2$$
     	O=S(=O)(NC1:C:C:C2:C(:C:1)OCCO2)C1:C:C:C(F):C(F):C:1 $$\not \in \mathcal{P}_2$$

   • $$\mathcal{P}_3 = \{\,p \in \mathcal{P}\,|\,$$eerste en laatste cijfer van $$p$$ zijn hetzelfde$$\ ^{(*)}\,\}$$

     (*) voorwaarde is niet voldaan als er geen cijfers voorkomen in $$p$$ en is voldaan als er slechts één cijfer voorkomt in $$p$$
     

     voorbeeld:	C3=C(C(C2CCN(CCCC(C1=CC=C(F)C=C1)=O)CC2)=O)C=CC(=C3)Cl $$\in \mathcal{P}_3$$
     	O=[N+]([O-])C1:C:C2:C(:C:C:1/C=N/N1:C:N:N:C:1)OCO2 $$\not \in \mathcal{P}_3$$

   • $$\mathcal{P}_4 = \{\,p \in \mathcal{P}\,|\,$$er is een groep van drie opeenvolgende letters waarvan er minstens één geen c of C is, die minstens drie keer herhaald$$^{(*)}$$ wordt in $$p\,\}$$

     (*) rekening houdend met verschil tussen hoofdletters en kleine letters; geen overlap tussen de herhalingen van de groepen
     

     voorbeeld:	O=c1cc(-c2ccc(OCc3ccccc3)cc2)oc2cc(OCc3ccccc3)cc(OCc3ccccc3)c12 $$\in \mathcal{P}_4$$
     	CCC(C)NC(=O)c1ccccc1NC(=O)CN(c1ccc(OC)cc1)S(C)(=O)=O $$\not \in \mathcal{P}_4$$

   Geef telkens een Unix commando waarin de reguliere expressie gebruikt wordt door een commando uit de grep familie om enkel de regels van het tekstbestand naar stdout te schrijven waarvan het patroon $$p$$ behoort tot $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$.

2. Bepaal als volgt de woorden $$w_1\ w_2\ w_3\ w_4$$ van een geheime boodschap:

   • het woord $$w_1$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_1 \cap \mathcal{P}_2$$

   • het woord $$w_2$$ staat op de unieke regel waarvan $$p$$ behoort tot $$ \mathcal{P}_2 \cap \mathcal{P}_3$$

   • het woord $$w_3$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_3  \cap \mathcal{P}_4$$

   • het woord $$w_4$$ staat op de unieke regel waarvan $$p$$ behoort tot $$\mathcal{P}_4 \cap \mathcal{P}_1$$

   Geef telkens een Unix commando waarin de reguliere expressies voor de verzamelingen $$\mathcal{P}_i\ (i = 1, 2, 3, 4)$$ gebruikt worden door commando's uit de grep familie om het woord $$w_j\ (j = 1, 2, 3, 4)$$ op te zoeken in het tekstbestand en uit te schrijven naar stdout. Hierbij is het niet toegelaten om het woord $$w_j$$ letterlijk uit te schrijven (bv. echo $$w_j$$).

   Opmerking

   Je moet echt wel een genie op vlak van chemie zijn om te achterhalen welke geheime boodschap in deze vier woorden verborgen zit, maar dat maakt geen deel uit van de opgave.