Any form of data is represented in computers and in telecommunication as a bitstring: a series of consecutive bits. A bit is the smallest unit of data, which can take two values: 0 or 1.

A communication protocol does not send bitstrings across a network all at once, but sends smaller packets of fixed length $$w$$, typically 8-bit octets (bytes; $$w = 8$$). In addition, an extra parity bit is added to each packet before transmission: an easy way to detect errors upon receipt if packets were modified during transmission. The parity bit ensures the total number of 1-bits in a packet is always even or odd. Accordingly, there are two variants of parity bits: even parity and odd parity.

Send

Suppose we want to send bitstring 010000111010110011100110101101111000010000 (42 bits) with a communication protocol using packets of length $$w = 8$$. First, the bitstring is split into packets of $$w - 1 = 7$$ bits. Then a parity bit is computed for each packet, and appended to the packet (indicated in green).

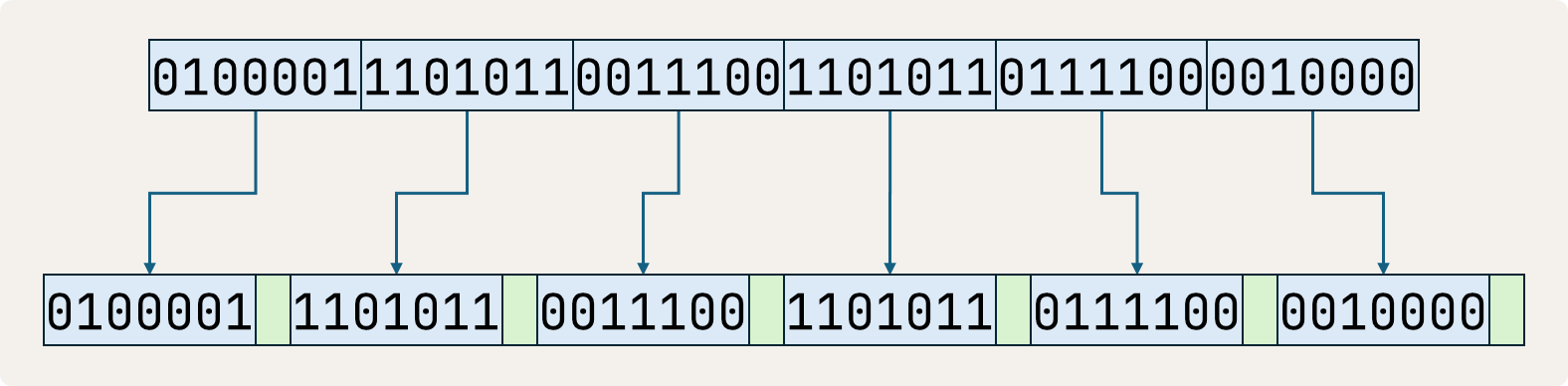
If the communication protocol uses even parity then the parity bit is set to 1 if the number of ones in a packet (without parity bit) is odd, making the total number of ones in the entire packet (including the parity bit) even. If the number of ones in a packet (without parity bit) was already even, the parity bit is set to 0.

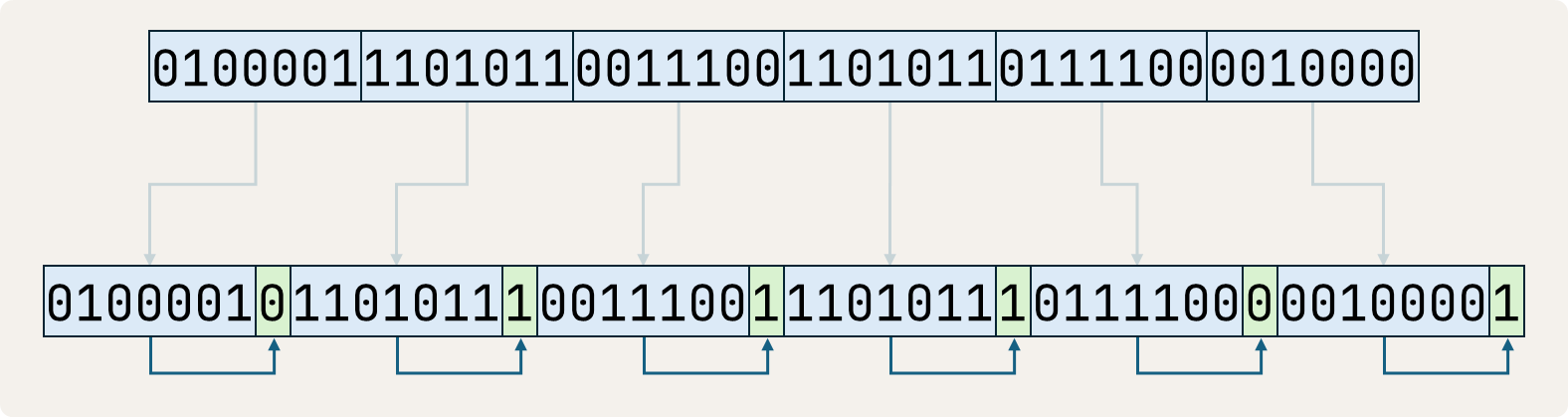
In case of odd parity, encoding is done the opposite way. If the number of ones in a packet with $$w - 1$$ bits is even then the parity bit is set to 1, making the total number of ones in the entire packet (including the parity bit) odd. If the number of ones in a packet (without parity bit) was already odd, then the parity bit is set to 0.

Receive

Upon receipt of a bitstring, the communication protocol first checks the parity for each packet of length $$w$$. With even parity, the number of ones in each packet (including the parity bit) must be even.

With odd parity, the number of ones in each packet (including the parity bit) must be odd.

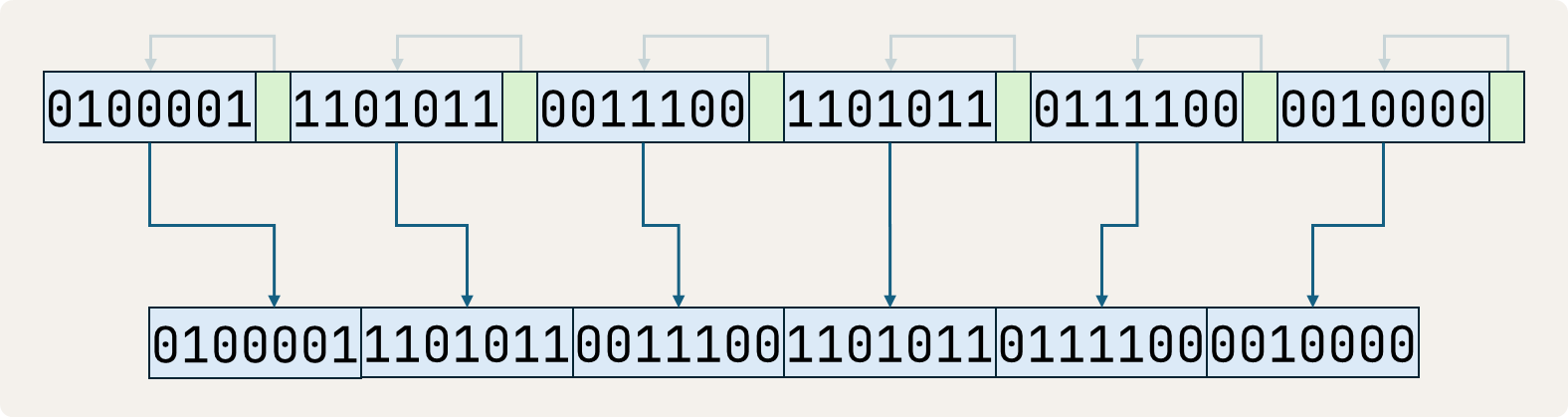
If the communication protocol finds the received bitstring to be valid, it removes all parity bits. This way, we get back the original bitstring from before parity bits were added upon transmission.

Input

Four lines respectively containing the following information for a bitstring to be sent by or received by a communication protocol:

1. the bitstring

2. the packet length $$w$$ of the protocol

3. even if the protocol uses even parity or odd if it used odd parity

4. send if the protocol must send the bitstring or receive if it received the bitstring

Output

If the communication protocol must send the bitstring, the bitstring length must be a multiple of $$w - 1$$. If this is not the case, the output must contain the message invalid bitstring. Otherwise, the output must contain the bitstring after parity bits were added.

If the communication protocol received the bitstring, the bitstring length must be a multiple of $$w$$ and each packet must have a valid parity bit. If this is not the case, the output must contain the message invalid bitstring. Otherwise, the output must contain the bitstring after parity bits were removed.

Example: send with even parity

Input:

010000111010110011100110101101111000010000
8
even
send

Output:

010000101101011100111001110101110111100000100001

Example: receive with odd parity

Input:

11111001001011101110010100111010011000101100001011110110111011111111001010111
11
odd
receive

Output:

1111100100011101110001001110101100010110001011110101110111111100101011

Example: receive invalid bitstring

The 12-bit packet marked in red contains an odd number of bits (7). This makes the received bitstring invalid, because the communication protocol works with even parity.

Input:

110100100011001110000100010111011110101001111000001111100110010000100101001111111111
12
even
receive

Output:

invalid bitstring