Choose a random number $$n \in \mathbb{N}$$. Form a new number $$n'$$ by writing the digits of the number $$n$$ backwards. Calculate the sum $$n + n'$$ of these numbers.
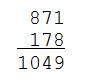
In most cases, repeating this procedure will eventually yield a palindrome:
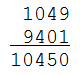
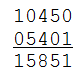
For some obscure reason, this doesn't apply to number 196 — at least, computer simulations that repeated the procedure until they got numbers of more than 300 million digits long, have never found a palindrome. Until this moment, nobody has found any sound proof for or against, so for now the answer to this question in unknown.
Assignment
A palindrome is a word, sentence or number or another sequence of characters that reads the same from left to right as from right to left. The term palindrome was introduced in the 17th century by the English author Ben Johnson, and is a compound of the Greek words palin (πάλιν, "again") and dromos (δρóμος, "direction").
-
Write a function palindrome to which a string must be given. The function must print a Boolean value that indicates whether the string given is a palindrome. When deciding if the string is symmetrical, the function should take into account all characters and it should also distinguish between uppercase and lowercase letters. Furthermore, the function has three optional parameters that can change this behaviour. A Boolean value can be given to each of these parameters, it's default value is True. The optional parameters have the following name, order and meaning:
-
digits: if the value False is given to this parameter, the function should ignore all digits in the string
-
other: if the value False is given to this parameter, the function should ignore all characters of the string that are not a letter or a digit
-
uppercasesensitive: if the value False is given to this parameter, the function shouldn't distinguish between lowercase and uppercase letters
-
Use the function palindrome to write a function stubborn, to which a number $$n \in \mathbb{N}$$ should be given. The function must print how many times the function above has to be repeated before it becomes a palindrome. Because there are values for which the procedure is likely not to become a palindrome, this function has an optional parameter maximum to which a number $$m \in \mathbb{N}$$ (default value: 1000) can be given. If the function hasn't found a palindrome after $$m$$ repetitions, the function should print the value $$m$$ as a result.
Example
>>> palindrome('a1b2c3c2b1a')
True
>>> palindrome('a1b2c3C2B1A')
False
>>> palindrome('a1b2c3C2B1A', uppercasesensitive=False)
True
>>> palindrome('a1b2c3c4b5a')
False
>>> palindrome('a1b2c3c4b5a', digits=False)
True
>>> palindrome('step on no pets')
True
>>> palindrome('Step on no pets')
False
>>> palindrome('Step on no pets', uppercasesensitive=False)
True
>>> palindrome("No 'x' in 'Nixon'", other=False, uppercasesensitive=False)
True
>>> stubborn(871)
3
>>> stubborn(196)
1000
>>> stubborn(196, maximum=200)
200
>>> stubborn(78552)
31
>>> stubborn(78552, maximum=25)
25