Ants mainly communicate with each other using odorants called pheromones. Like other insects, ants perceive smells with their long, thin, and mobile antennae. The paired antennae provide information about the direction and intensity of scents. Since most ants live on the ground, they use the soil surface to leave pheromone trails that may be followed by other ants. A forager that finds food, marks a trail on the way back to the colony. If this trail is followed by other ants, these ants then reinforce the trail when they head back with food to the colony. When the food source is exhausted, no new trails are marked by returning ants and the scent slowly dissipates.

Foraging ants travel distances of up to 200 meters from their nest and scent trails allow them to find their way back even in the dark. Distances traveled are measured using an internal pedometer that keeps count of the steps taken and also by evaluating the movement of objects in their visual field. Directions are measured using the position of the sun. They integrate this information to find the shortest route back to their nest. Ants that become separated from pheromone trails (for example because they have been moved to another location by a human being) may run around continuously until they die of exhaustion.

Assignment

In this assignment we simulate the behaviour of an ant tracking its way back to the nest by following a disturbed pheromone trail. The environment in which the ant forages is represented by a square $$n \times n$$ grid having $$n$$ row and $$n$$ columns. The ant initially is located in the bottom left corner of the grid and its nest is located in the top right corner of the grid. Each cell in the grid contains a pheromone trail that points up, down, left or right. On each turn in the simulation, the ant moves to the neighbouring cell that is pointed to by the pheromone trail, and then the direction of the trail on the cell that it has left turns 90° clockwise. If the ant is not able to move in the indicated direction because the edge of the grid blocks its path, it remains on its current cell and the direction of the trail on the cell turns 90° clockwise.

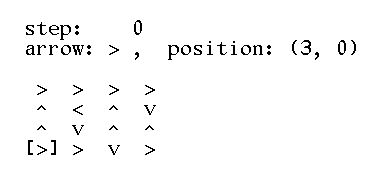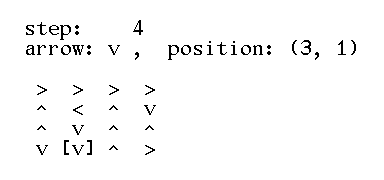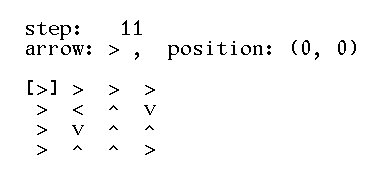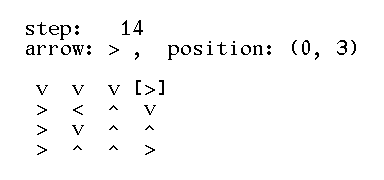
The original configuration of a square $$n \times n$$ grid with pheromone trails is stored in a text file. The file contains $$n$$ lines, with each line having $$n$$ direction symbols that are separated from each other by a single space. The following four characters are used as direction symbols:

• >: the pheromone trail points to the right

• <: the pheromone trail points to the left

• ^: the pheromone trail points up

• v: the pheromone trail points down

You are asked to define a class DrunkenAnt that can be used to simulate the behaviour of an ant. The objects of this class must support at least the following methods:

• An initialization method that takes the location of a text file. This file contains the original configuration of a square $$n \times n$$ grid with pheromone trails. Initially the ant is located at the bottom left corner of the grid.

• A method position that returns the current position of the ant in the grid. The rows of the grid are indexed top to bottom, and the columns from left to right, with indexing starting from zero. Each position in the grid is represented as a tuple whose first element indicates the row index and whose second element indicates the column index.

• A method __repr__ that returns a string representation of the current status of the environment. This string representation represents a square $$n \times n$$ grid in the same format as used to store the original configuration of the grid in a text file. Note that by simulating the steps of the ant, the direction symbols in the grid may have changed with respect to the initialization of the object.

• A method step that can be used to perform a single simulation step. The method must return the new position of the ant after a single step of the ant has been simulated.

• A method steps that can be used to perform an entire simulation of the steps taken by the ant from its current position until it reaches its nest at the top right corner of the grid. The method must return a list of positions that starts with the original position of the ant at the start of the simulation, followed by the positions of the ant after each step in the simulation.

• A method __str__ that returns a string representation of the current status of the environment, which also indicates the current position of the ant in the grid. In contrast to the string representation returned by the method __repr__, the direction symbols on each line are no longer separated by spaces, but each direction symbol is preceded and followed by a single space. Instead of using spaces, the direction symbol at the current location of the ant is preceded by an opening square bracket ([) and followed by a closing square bracket (]).

Example

In the following interactive session we assume that the text file square.txt¹ is located in the current directory.

>>> ant = DrunkenAnt('square.txt')
>>> ant.position()
(3, 0)
>>> ant
> > > >
^ < ^ v
^ v ^ ^
> > v >
>>> print(ant)
 >  >  >  > 
 ^  <  ^  v 
 ^  v  ^  ^ 
[>] >  v  > 

>>> ant.step()
(3, 1)
>>> ant.position()
(3, 1)
>>> ant
> > > >
^ < ^ v
^ v ^ ^
v > v >
>>> print(ant)
 >  >  >  > 
 ^  <  ^  v 
 ^  v  ^  ^ 
 v [>] v  > 

>>> ant.step()
(3, 2)
>>> ant.position()
(3, 2)
>>> ant
> > > >
^ < ^ v
^ v ^ ^
v v v >
>>> print(ant)
 >  >  >  > 
 ^  <  ^  v 
 ^  v  ^  ^ 
 v  v [v] > 

>>> ant.steps()
[(3, 2), (3, 2), (3, 1), (3, 1), (3, 0), (3, 0), (3, 0), (2, 0), (1, 0), (0, 0), (0, 1), (0, 2), (0, 3)]
>>> ant.position()
(0, 3)
>>> print(ant)
 v  v  v [>]
 >  <  ^  v 
 >  v  ^  ^ 
 >  ^  ^  >