Resistors are passive two-terminal electrical components that implement electrical resistance as a circuit element. In electronic circuits, resistors are used to reduce current flow, adjust signal levels, divide voltages, bias active elements, and terminate transmission lines, among other uses.

The electronic color code (current international standard: IEC 60062:20161) is used to indicate the strength of a resistor. A resistor is marked with three, four or five colored bands because in repairing mounted resistors it turned out that it was not always easy to read printed text on these small components. Especially if the printed side was not clearly visible because it was directed towards the chassis or another component. However, colored bands also have their drawbacks, especially for color blind people. Overheating of a resistor or dirt accumulation may also make it impossible to distinguish brown from red or orange.
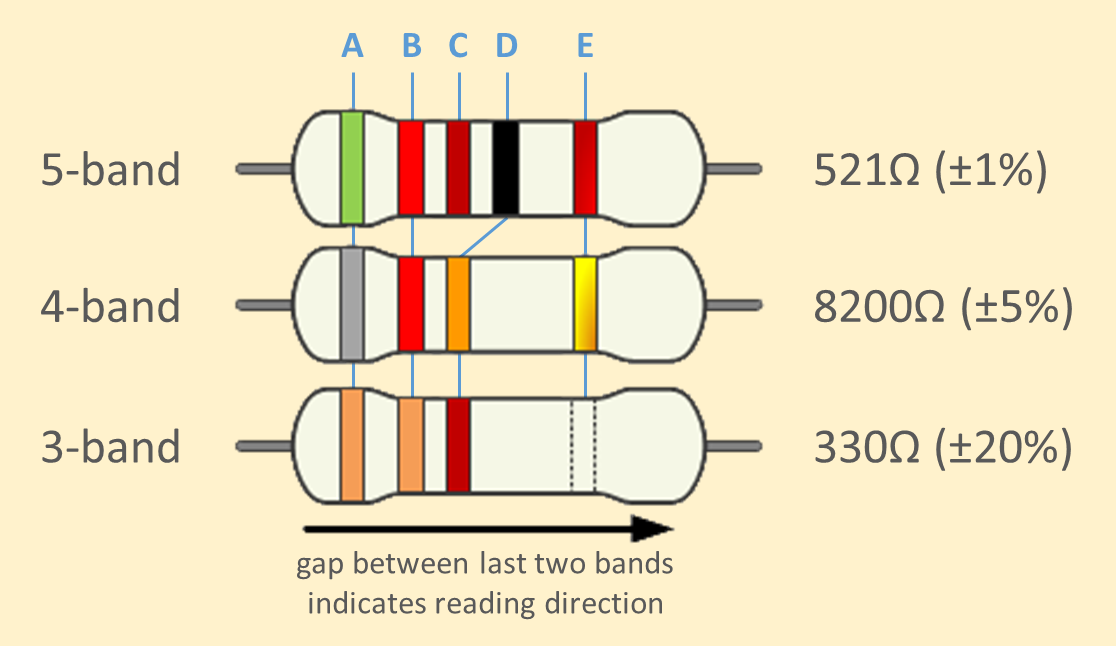
To distinguish left from right there is a wider gap between the penultimate (C/D) and the last (E) band. The strength of the resistor is encoded by the colored bands in the following way:
-
band A is the first significant digit of the strength
-
band B is the second significant digit of the strength
-
band C is the third significant digit of the strength (this band is optional)
-
band D is the decimal multiplier
-
band E indicates the tolerance of the strength in percent (this band is optional)
The IEC 60062:20162 standard prescribes the following color codes:
| color | significant digit | multiplier | tolerance (%) |
|---|---|---|---|
| (none) | - | - | 20 |
| PINK | - | $$\times 10^{-3}$$ | - |
| SILVER | - | $$\times 10^{-2}$$ | 10 |
| GOLD | - | $$\times 10^{-1}$$ | 5 |
| BLACK | 0 | $$\times 10^{0}$$ | - |
| BROWN | 1 | $$\times 10^{1}$$ | 1 |
| RED | 2 | $$\times 10^{2}$$ | 2 |
| ORANGE | 3 | $$\times 10^{3}$$ | - |
| YELLOW | 4 | $$\times 10^{4}$$ | - |
| GREEN | 5 | $$\times 10^{5}$$ | 0.5 |
| BLUE | 6 | $$\times 10^{6}$$ | 0.25 |
| VIOLET | 7 | $$\times 10^{7}$$ | 0.1 |
| GRAY | 8 | $$\times 10^{8}$$ | 0.05 |
| WHITE | 9 | $$\times 10^{9}$$ | - |
As in a rainbow the colors are sorted in the order of the visible light spectrum: red (2), orange (3), yellow (4), green (5), blue (6) and violet (7). Black (0) has no energy, brown (1) has a little more, white (9) has everything and gray (8) is like white, but less intense. Lee Sallows designed this ingenious rainbow table based on the electronic color code:

The table maps the letters on its top row onto the numbers 1, 2, …, 9 and the letters on its bottom row onto the numbers -1, -2, …, -9. What's so clever is that this mapping of letters onto numbers is such that if we add the values of all letters in the names of the colors in the electronic color code, the obtained sum always corresponds to the significant digit the standard assigns to this color. This way, the table forms some kind of reflexive rainbow.
| B+L+A+C+K | = | -4+7+6-7-2 | = | 0 |
| B+R+O+W+N | = | -4+9-9+8-3 | = | 1 |
| R+E+D | = | +9-1-6 | = | 2 |
| O+R+A+N+G+E | = | -9+9+6-3+1-1 | = | 3 |
| Y+E+L+L+O+W | = | -8-1+7+7-9+8 | = | 4 |
| G+R+E+E+N | = | +1+9-1-1-3 | = | 5 |
| B+L+U+E | = | -4+7+4+1 | = | 6 |
| V+I+O+L+E+T | = | +3+5-9+7-1+2 | = | 7 |
| G+R+A+Y | = | +1+9+6-8 | = | 8 |
| W+H+I+T+E | = | +8-5+5+2-1 | = | 9 |
Assignment
The value of a word (int) is the integer that is obtained by adding the values of the individual letters of the word. The value of a letter (int) is derived from a sequence containing $$2n$$ letters ($$n \in \mathbb{N}_0$$) that successively have values $$-n, \ldots, -2, -1, 1, 2, \ldots, n$$ (note that zero is missing in this sequence). In determining the value of a word, no distinction is made between uppercase and lowercase letters.
All functions in this assignment take a sequence (str, list or tuple) containing an even number of different letters (str). In case this argument is not a sequence containing an even number of letters without duplicates (no distinction made between uppercase and lowercase letters), an AssertionError must be raised with the message invalid letters. This AssertionError takes precedence over all other exceptions that may be raised by the functions.
In addition, some functions take a word (str) or a sequence (list or tuple) of words (str). These functions must explicitly check that each word is a string that only contains letters occurring in the given sequence of letters (no distinction made between uppercase and lowercase letters). If this is not the case, an AssertionError must be raised with the message invalid word.
Your task:
-
Write a function letter_value that takes a sequence containing an even number of different letters. The function must return a dictionary (dict) that maps each letter (str) in the given sequence onto its corresponding value (int). All keys in this dictionary must be uppercase letters.
-
Write a function word_value that takes two arguments: a word (str) and a sequence containing an even number of different letters. The function must return the value of the given word (int), with the value of the individual letters derived from the given letter sequence.
-
Write a function rainbow that takes two arguments: a sequence containing $$m \in \mathbb{N}$$ words and a sequence containing an even number of different letters. The function must return a Boolean value (bool) that indicates whether the words in the given sequence successively have values $$0, 1, \ldots, m - 1$$. The value of the given words must be derived from the given letter sequence.
-
Write a function reflected that takes two arguments: a sequence of words and a sequence containing an even number of different letters. The function must return a tuple containing the words from the given sequence sorted according to increasing value. The value of the given words must be derived from the given letter sequence. Words having the same value must be sorted alphabetically, without making distinction between uppercase and lowercase letters.
None of these functions may ever change any arguments passed to them.
Example
>>> letter_value('OYCDHBNKEgtvuialwr')
{'O': -9, 'Y': -8, 'C': -7, 'D': -6, 'H': -5, 'B': -4, 'N': -3, 'K': -2, 'E': -1, 'G': 1, 'T': 2, 'V': 3, 'U': 4, 'I': 5, 'A': 6, 'L': 7, 'W': 8, 'R': 9}
>>> letter_value('abc')
Traceback (most recent call last):
AssertionError: invalid letters
>>> letter_value('abba')
Traceback (most recent call last):
AssertionError: invalid letters
>>> word_value('black', 'OYCDHBNKEGTVUIALWR')
0
>>> word_value('BROWN', 'oycdhbnkeGTVUIALWR')
1
>>> word_value('red', 'OYCDHBNKEgtvuialwr')
2
>>> word_value('SILVER', 'OYCDHBNKEGTVUIALWR')
Traceback (most recent call last):
AssertionError: invalid word
>>> rainbow(['BLACK', 'brown', 'RED', 'orange', 'YELLOW', 'green', 'BLUE', 'violet', 'GRAY', 'White'], 'OYCDHBNKEgtvuialwr')
True
>>> rainbow(['BLACK', 'YELLOW', 'violet', 'green', 'White', 'orange', 'GRAY', 'BLUE', 'RED', 'brown'], 'OYCDHBNKEgtvuialwr')
False
>>> rainbow(('BLACK', 'brown', 'RED', 'orange', 'YELLOW', 'green', 'BLUE', 'violet', 'GRAY', 'White'), 'bwdiucankYOGTHELRV')
False
>>> colors = ['BLACK', 'YELLOW', 'violet', 'green', 'White', 'orange', 'GRAY', 'BLUE', 'RED', 'brown']
>>> reflected(colors, 'OYCDHBNKEgtvuialwr')
('BLACK', 'brown', 'RED', 'orange', 'YELLOW', 'green', 'BLUE', 'violet', 'GRAY', 'White')
>>> colors
['BLACK', 'YELLOW', 'violet', 'green', 'White', 'orange', 'GRAY', 'BLUE', 'RED', 'brown']
>>> colors = ('BLACK', 'YELLOW', 'violet', 'green', 'White', 'orange', 'GRAY', 'BLUE', 'RED', 'brown')
>>> reflected(colors, 'bwdiucankYOGTHELRV')
('BLACK', 'brown', 'BLUE', 'White', 'RED', 'GRAY', 'orange', 'YELLOW', 'green', 'violet')