Consider a building with a flat square roof having size $$3^k \times 3^k$$ ($$k \in \mathbb{N_0}$$) metres and sides parallel to north-south and east-west directions. The roof is covered with square tiles having sides of length 1 metre. One of the tiles has been removed, so that there is a hole in the roof big enough to fall in. The tiles form a rectangular mesh on the roof, so their positions may be specified with $$(x, y)$$ co-ordinates. The tile at the southwestern corner has co-ordinates $$(1, 1)$$. The first co-ordinate increases while going eastwards, and the second co-ordinate increases while going northwards.
A sleepwalker wanders across the roof, in each step moving from the tile he is standing on to the adjacent tile on the east (E), west (W), south (S) or north (N). The sleepwalker roof ramble starts from the southwestern corner tile. The description of his path is a word $$d_k$$ containing the letters N, S, E and W denoting respectively a step to the north, south, east and west. For $$k = 1$$ the word describing the path of the sleepwalker is
$$d_1$$ = EENNWSWN
For $$k = 2$$ the word describing the path of the sleepwalker is
| $$d_2$$ = | NNEESWSEENNEESWSEEEENNWSWNNEENNWSWNNEENN |
| WSWNWWWSSENESSSSWWNENWWSSWWNENWNEENNWSWN |
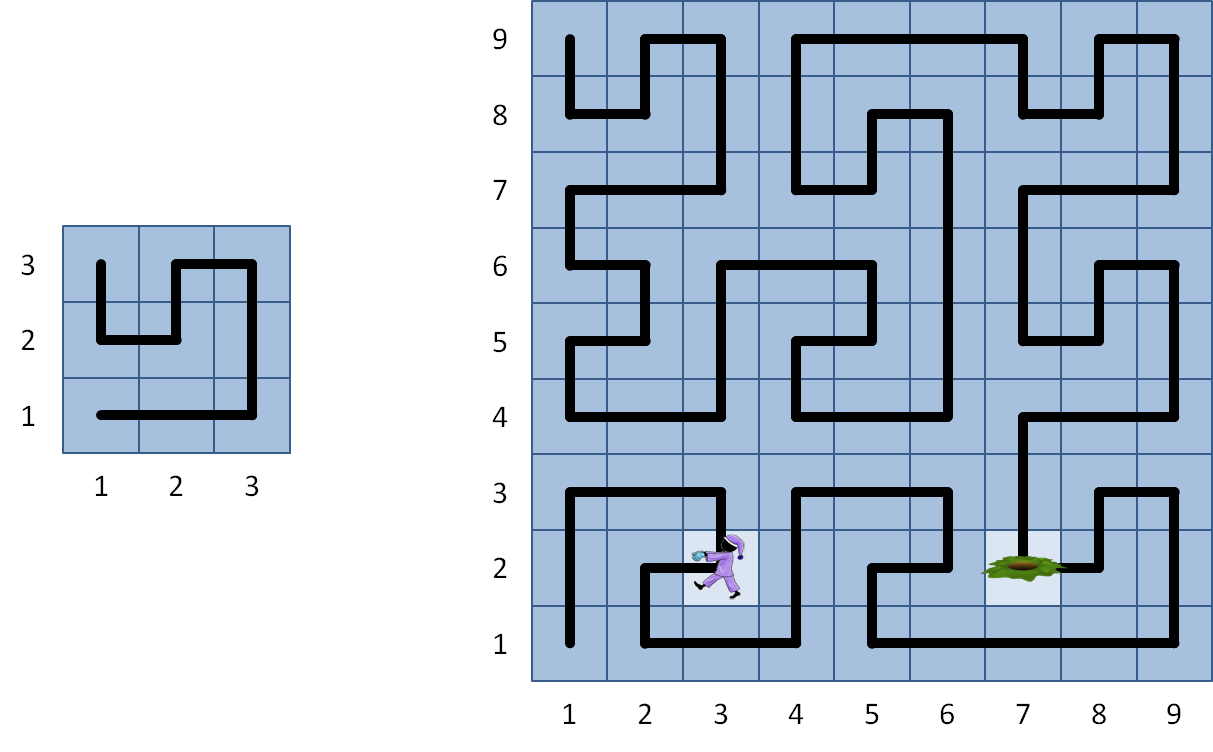
The following pictures shows how the sleepwalker would go across a roof of dimensions $$3 \times 3$$ (left) and $$9 \times 9$$ (right).
Generally, if $$k \geq 1$$ the description of a sleepwalker's path on a roof of dimension $$3^{k+1} \times 3^{k+1}$$ voor $$k \geq 1$$ is described by the word
$$d_{k + 1}$$ = $$p_a(d_k)$$ E $$p_a(d_k)$$ E $$d_k$$ N $$d_k$$ N $$d_k$$ W $$p_c(d_k)$$ S $$p_b(d_k)$$ W $$p_b(d_k)$$ N $$d_k$$
where functions $$p_a$$, $$p_b$$ en $$p_c$$ denote
the following permutations of the directions
| E | W | N | S | |
|---|---|---|---|---|
| $$p_a$$ | N | S | E | W |
| $$p_b$$ | S | N | W | E |
| $$p_c$$ | W | E | S | N |
We have for example that $$p_a$$(SEN) = WNE, $$p_b$$(SEN) = ESW and $$p_c$$(SEN) = NWS.
Assignment
We start observing the sleepwalker at the moment he stands on the tile at co-ordinates $$(s_x, s_y)$$. After how many steps will the sleepwalker fall into the hole made after removing the tile at co-ordinates $$(g_x, g_y)$$. In order to answer this question, the following procedure must be followed
Write a function permutation that takes two string arguments. The first argument must be a word containing directions (a string that only contains the letters N, S, E and W). The second argument must be one of the letters a, b, or c. This letter indicates whether the function permutation must respectively return the result of the permutation $$p_a$$, $$p_b$$ or $$p_c$$.
Write a function path that takes an integer $$k \in \mathbb{N_0}$$. The function must return a string that contains the word of directions that is followed by a sleepwalker on a roof having size $$3^k \times 3^k$$.
Write a function sleepwalker that computes the number of steps that a sleepwalker will make before he falls into the hole. This function takes five arguments. The first argument is an integer $$k \in \mathbb{N_0}$$ that determines the size of the roof ($$3^k \times 3^k$$). The next two arguments respectively represent the co-ordinates $$s_x$$ and $$s_y$$ of the tile the sleepwalker is standing on at the moment the observation starts. The final two arguments are the co-ordinates $$g_x$$ and $$g_y$$ of the tile that has been removed.
Example
>>> permutation('SEN', 'a')
'WNE'
>>> permutation('SEN', 'b')
'ESW'
>>> permutation('SEN', 'c')
'NWS'
>>> path(1)
'EENNWSWN'
>>> path(2)
'NNEESWSEENNEESWSEEEENNWSWNNEENNWSWNNEENNWSWNWWWSSENESSSSWWNENWWSSWWNENWNEENNWSWN'
>>> route = path(3)
>>> print('\\n'.join(route[x:x + 80] for x in range(0, len(route), 80)))
EENNWSWNNEENNWSWNNNNEESWSEENNEESWSEENNEESWSESSSWWNENWWWWSSENESSWWSSENESENNEESWSE
EEENNWSWNNEENNWSWNNNNEESWSEENNEESWSEENNEESWSESSSWWNENWWWWSSENESSWWSSENESENNEESWS
EENNEESWSEENNEESWSEEEENNWSWNNEENNWSWNNEENNWSWNWWWSSENESSSSWWNENWWSSWWNENWNEENNWS
WNNNNEESWSEENNEESWSEEEENNWSWNNEENNWSWNNEENNWSWNWWWSSENESSSSWWNENWWSSWWNENWNEENNW
SWNNNNEESWSEENNEESWSEEEENNWSWNNEENNWSWNNEENNWSWNWWWSSENESSSSWWNENWWSSWWNENWNEENN
WSWNWSSWWNENWWSSWWNENWWWWSSENESSWWSSENESSWWSSENESEEENNWSWNNNNEESWSEENNEESWSESWWS
SENESSWWSSENESSWWSSENESSSSWWNENWWSSWWNENWWSSWWNENWNNNEESWSEEEENNWSWNNEENNWSWNWSS
WWNENWWWWSSENESSWWSSENESSSSWWNENWWSSWWNENWWSSWWNENWNNNEESWSEEEENNWSWNNEENNWSWNWS
SWWNENWNNNEESWSEENNEESWSEEEENNWSWNNEENNWSWNNEENNWSWNWWWSSENESSSSWWNENWWSSWWNENWN
EENNWSWN
>>> sleepwalker(2, 3, 2, 7, 2)
20
>>> sleepwalker(2, 9, 6, 3, 7)
43
>>> sleepwalker(3, 1, 1, 1, 27)
728