Ongekende variantie op de metingen

Tot nog toe werd verondersteld dat de populatievariantie $\sigma^2$ gekend is bij het berekenen van een betrouwbaarheidsinterval voor $\mu$. Betrouwbaarheidsintervallen voor $\mu$ werden dan opgebouwd door op te merken dat de gestandaardiseerde waarde $(\bar{X} - \mu)/(\sigma/\sqrt{n})$ standaardnormaal verdeeld is en bijgevolg

\[\begin{equation*} \left[\mu - 1.96 \frac{\sigma}{\sqrt{n}},\mu + 1.96 \frac{\sigma}{\sqrt{n}}% \right] \end{equation*}\]

een 95% referentie-interval voor het steekproefgemiddelde voorstelt.

In de praktijk komt het quasi nooit voor dat men de populatievariantie $\sigma^2$ exact kent. In de praktijk wordt deze geschat als $S^2$ op basis van de voorhanden zijnde steekproef. Als gevolg hiervan zullen de betrouwbaarheidsintervallen uit voorgaande sectie doorgaans iets te smal zijn (omdat ze er geen rekening mee houden dat ook de variantie werd geschat) en is het noodzakelijk om bij de berekening $(\bar{X} - \mu)/(S/\sqrt{n})$ te gebruiken als gestandaardiseerde waarde i.p.v. $(\bar{X} - \mu)/(\sigma/\sqrt{n})$. Wanneer de steekproef voldoende groot is, ligt de vierkantswortel van variantie $S^2$ voldoende dicht bij $\sigma$ zodat ${(\bar{X} - \mu)}/{(S/\sqrt{n}) }$ bij benadering een standaardnormale verdeling volgt en, bijgevolg,

\[\begin{equation*} \left[\bar{X} - z_{\alpha/2} \ \frac{S}{\sqrt{n}} , \bar{X} + z_{\alpha/2} \ \frac{S}{\sqrt{n}}\right] \end{equation*}\]

een benaderd $(1- \alpha)100\%$ betrouwbaarheidsinterval is voor $\mu$. Voor kleine steekproeven is dit niet langer het geval. Daardoor introduceert men een extra onnauwkeurigheid in de gestandaardiseerde waarde ${(\bar{X} - \mu)}/{(S/\sqrt{n})}$. Deze is nog wel gecentreerd rond nul en symmetrisch, maar niet langer Normaal verdeeld. De echte verdeling voor eindige steekproefgrootte $n$ heeft zwaardere staarten dan de Normale. Hoeveel zwaarder de staarten zijn, hangt van de steekproefgrootte $n$ af. Als $n$ oneindig groot wordt, komt $S$ zodanig dicht bij $\sigma$ te liggen dat de extra onnauwkeurigheid in de gestandaardiseerde waarde verwaarloosbaar is en bijgevolg ook het verschil met de Normale verdeling. Maar voor relatief kleine steekproeven hangt de verdeling van ${(\bar{X} - \mu)}/({S/\sqrt{n}})$ af van de grootte $n$ van de steekproef. Ze krijgt de naam (Student) $t$-verdeling met $n-1$ vrijheidsgraden (in het Engels: degrees of freedom). Deze verdeling wordt voor een aantal verschillende vrijheidsgraden geïllustreerd in Figuur 19. De t-verdelingen in de figuur hebben duidelijk bredere staarten dan de normaalverdeling, waardoor ze ook een grotere percentielwaarden hebben voor een vooropgesteld betrouwbaarheidsniveau. Dat zal leiden tot bredere intervallen, wat logisch is aangezien we de extra onzekerheid inbouwen die gerelateerd is aan het schatten van de standaarddeviatie.

Definitie 26 (t-verdeling)

Als $X_1, X_2, ..., X_n$ een steekproef vormen uit de Normale verdeling $N(\mu, \sigma^2)$, dan is $(\bar{X} - \mu)/(S/\sqrt{n})$ verdeeld als een $t$-verdeling met $n-1$ vrijheidsgraden.

**Einde Definitie

grid <- seq(-5,5,.1)
densDist <- cbind(grid,dnorm(grid), sapply(c(2,5,10),dt,x=grid))
colnames(densDist) <- c("x","normal",paste0("t",c(2,5,10)))

densDist %>%
  as.data.frame %>%
  gather(dist,dens,-x) %>%
  ggplot(aes(x=x,y=dens,color=dist)) +
  geom_line() +
    xlab("x") +
  ylab("Densiteit")

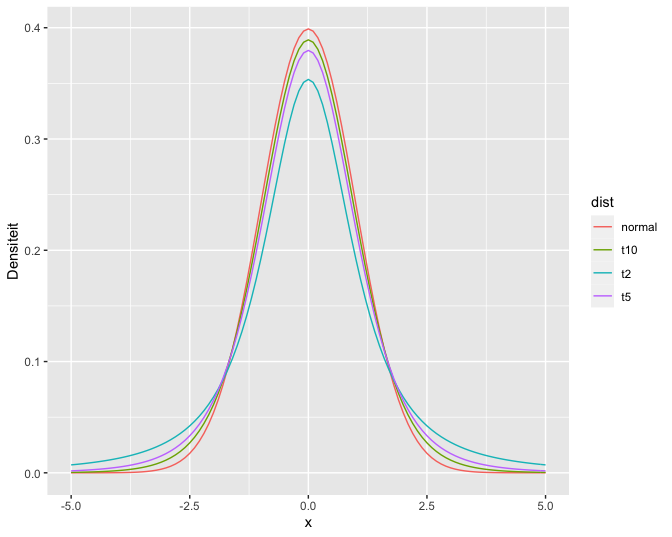
Figuur 19: Normale verdeling en t-verdeling met verschillende vrijheidsgraden.

Percentielen van de $t$-verdeling kunnen niet met de hand berekend worden, maar kan men voor de verschillende waarden van $n$ aflezen in Tabellen of berekenen in R. In de onderstaande code wordt het 95%, 97.5%, 99.5% percentiel berekend voor een t-verdeling met 14 vrijheidsgraden, die gebruik kunnen worden voor de berekening van 90%, 95% en 99% betrouwbaarheidsintervallen.

qt(.975,df=14)

## [1] 2.144787

qt(c(.95,.975,.995),df=14)

## [1] 1.761310 2.144787 2.976843

We zien dat het 97.5% percentiel 2.14 voor een t-verdeling met $n-1=14$ vrijheidsgraden inderdaad groter is dan het kwantiel uit de normaal verdeling 1.96.

Een gelijkaardige logica als voor de Normale verdeling met gekende variantie, geeft dan aan dat een $100\% (1-\alpha)$ betrouwbaarheidsinterval voor het gemiddelde $\mu$ van een Normaal verdeelde veranderlijke $X$ met onbekende variantie kan berekend worden als

\[\begin{equation*} \left[\bar{X} - t_{n-1, \alpha/2} \frac{s}{\sqrt{n}} , \bar{X} + t_{n-1, \alpha/2} \frac{s}{\sqrt{n}}\right] \end{equation*}\]

Deze uitdrukking verschilt van deze in de vorige sectie doordat het $(1-\alpha/2)100\%$ percentiel van de Normale verdeling wordt vervangen door het $(1-\alpha/2)100\%$ percentiel van de t-verdeling met $n-1$ vrijheidsgraden.

Captopril voorbeeld

Voor het captopril voorbeeld kunnen we dus een 95% betrouwbaarheidsinterval bekomen door

mean(delta) -  qt(.975,df=14)*sd(delta)/sqrt(n)

## [1] -23.93258

mean(delta) + qt(.975,df=14)*sd(delta)/sqrt(n)

## [1] -13.93409

Een 99% betrouwbaarheidsinterval voor gemiddelde bloeddrukverandering wordt als volgt bekomen:

mean(delta) -  qt(.995,df=14)*sd(delta)/sqrt(n)

## [1] -25.87201

mean(delta) + qt(.995,df=14)*sd(delta)/sqrt(n)

## [1] -11.99466

Interpretatie van betrouwbaarheidsintervallen

We zullen opnieuw steekproeven trekken van de grote NHANES studie en deze keer BI’s bestuderen voor log2-cholesterol steekproefwaarden. We voeren eerst herhaalde experimenten uit met steekproefgrootte 10.

res$n <- as.character(res$n) %>%
  as.double(res$n)

res$ll <- res$mean-qt(0.975,df=res$n-1)*res$se
res$ul <- res$mean+qt(0.975,df=res$n-1)*res$se

mu <- fem$DirectChol%>%log2%>%mean

res$inside <- res$ll<=mu & mu<=res$ul
res$n <- as.factor(res$n)

res %>%
  group_by(n) %>%
  summarize(coverage=mean(inside)) %>%
  spread(n,coverage)

## # A tibble: 1 × 3
##    `10`  `50` `100`
##   <dbl> <dbl> <dbl>
## 1 0.949 0.947 0.959

We zien dat de omvang van de intervallen nu worden gecontroleerd op hun nominale betrouwbaarheidsniveau van 95%.

res %>%
  filter(n==10) %>%
  slice(1:20) %>%
  ggplot(aes(x=sample,y=mean,color=inside)) +
  geom_point() +
  geom_errorbar(
    aes(ymin=mean-qt(0.975,df=9)*se,
    ymax=mean+qt(0.975,df=9)*se))+
  geom_hline(yintercept = fem$DirectChol %>% log2 %>% mean) +
  ggtitle("20 CI for N=10") +
  ylim(range(fem$DirectChol %>% log2))

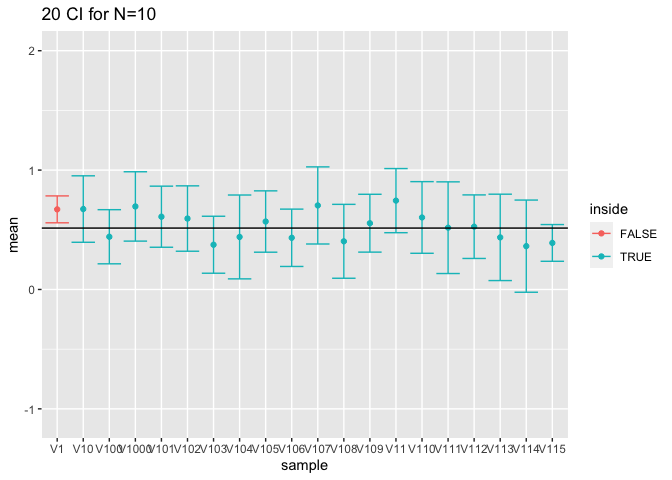
Figuur 20: Interpretatie van 95$$\%$$ betrouwbaarheidintervallen. Resultaten op basis van 20 gesimuleerde steekproeven. We zien in de figuur duidelijk dat het populatiegemiddelde vast is maar ongekend (volle zwarte lijn) en dat de bovengrens en ondergrens van betrouwbaarheidsintervallen voor het populatiegemiddelde varieert van steekproef tot steekproef.

De simulatiestudie toont dus op een empirische wijze aan dat de constructie correct is. Het demonstreert bovendien de interpretatie van probabiliteit via herhaalde steekproefname. In Figuur 20 wordt de interpretatie ook grafisch weergegeven voor de eerste 20 gesimuleerde steekproeven. De figuur toont duidelijk aan dat het werkelijke populatiegemiddelde vast is maar ongekend. Het wordt geschat aan de hand van het steekproefgemiddelde dat at random varieert van steekproef tot steekproef rond het werkelijk gemiddelde. We zien ook dat de grenzen van de betrouwbaarheidsintervallen variëren van steekproef tot steekproef. Daarnaast varieert de breedte van de betrouwbaarheidsintervallen eveneens omdat de steekproefstandaarddeviatie eveneens varieert van steekproef tot steekproef[29].

In de praktijk zullen we op basis van 1 steekproef besluiten dat het betrouwbaarheidsinterval het populatiegemiddelde bevat en we weten dat dergelijke uitspraken met een kans van $1-\alpha$ (hier 95%) correct zijn.

Opdracht

Voer de bovenstaande simulatie studie opnieuw uit maar verdubbel de steekproefgrootte. Welke impact heeft dit op de BIs?