Lemmings — a species of small rodents — are known to have periodic population booms. They reproduce so quickly that their population fluctuations are chaotic,12 rather than following linear growth to a carrying capacity or regular oscillations. It is not known why lemming populations fluctuate with such great variance roughly every four years, before numbers drop to near extinction. If an overpopulation of lemmings occurs in a certain area, they disperse in all directions, seeking food and shelter their natural habitats can no longer provide. These mass migrations are so striking that lemmings have become the subject of widely popular misconceptions that go back many centuries. In the 1530s, the geographer Zeigler of Strasbourg proposed the theory that the creatures fell out of the sky during stormy weather (also featured in the folklore of the Inupiat/Yupik at Norton Sound), and then died suddenly when the grass grew in spring. This description was contradicted by the natural historian Ole Worm, who accepted that lemmings could fall out of the sky, but claimed they had been brought over by the wind rather than created by spontaneous generation.3
The misconception of lemming "mass suicide" is long-standing and has been popularized by a number of factors. Most influential was the 1958 Disney film White Wilderness4 — which won an Academy Award for Documentary Feature — in which footage was shown with lemmings jumping into certain death after scenes of mass migration. However, the documentary Cruel Camera5 found out that the lemmings used for White Wilderness were flown from Hudson Bay to Calgary, Alberta, Canada, where they did not jump off the cliff, but were in fact forced off the cliff by the camera crew. Because of the limited number of lemmings at their disposal, which in any case were the wrong subspecies, the migration scenes were simulated using tight camera angles and a large, snow-covered turntable.

These stories about lemmings inspired the Scottish software company DMA Design6 (currently known as Rockstar North Ltd.) to develop the video game Lemmings7. Lemmings was one of the best-received video games of the early 1990s. The objective of the game is to guide a group of anthropomorphised lemmings through a number of obstacles to a designated exit. Each level begins with a trap door opening from above, releasing a steady line of lemmings who all follow each other. To save the required number of lemmings to win, one must determine how to assign a limited number of eight different skills to specific lemmings that allow the selected lemming to alter the landscape, to affect the behaviour of other lemmings, or to clear obstacles to create a safe passage for the rest of the lemmings.
Assignment
In this assignment we ask you to perform a simplified simulation of a lemming in a level of the video game Lemmings. A level of the video game consists of a number of cells that are arranged in a rectangular grid, and is described in a text file. In that description free cells are represented by a space, and cells containing an obstacle are represented by a hash symbol (#). Cells along the outer edge of the grid always contain an obstacle. A level might thus be represented in the following way.
################################# # # # # # # ### # ########### ### # ########### ######## # ########### ############## # #################################
Because each level has a rectangular shape, we will indicate positions of cells in the level by numbering the rows of the rectangle from top to bottom, and the columns from left to right, starting from zero. For our example level, the rows and columns are numbered as follows.
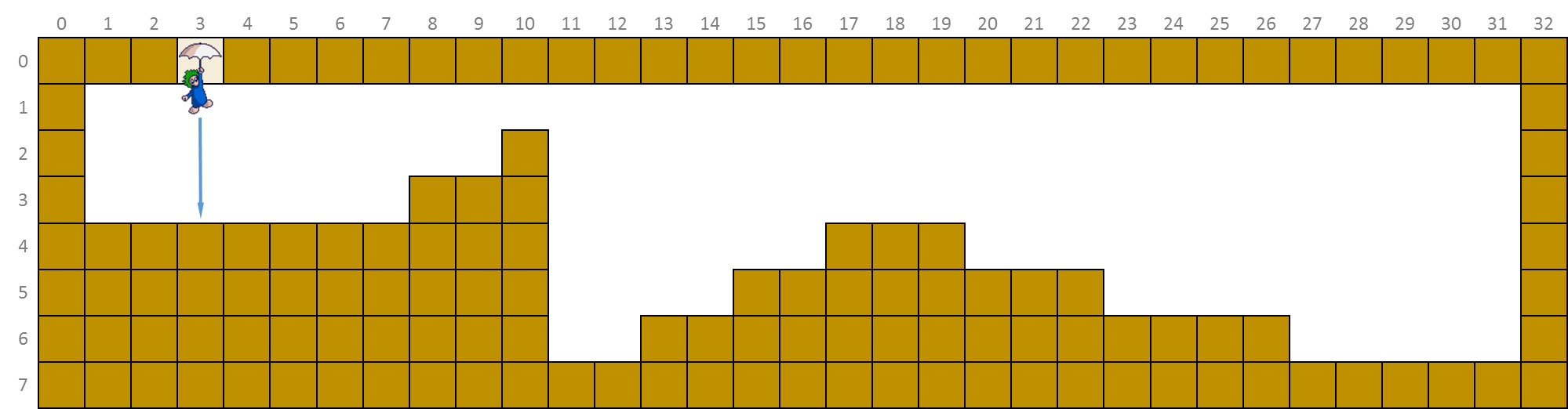
If we drop a lemming in the level through a trap door opening from above in column 3, the lemming falls down until it hits solid ground at position $$(3, 3)$$. If the lemming initially starts moving towards the left, the situation of the level at that point in time looks like this.
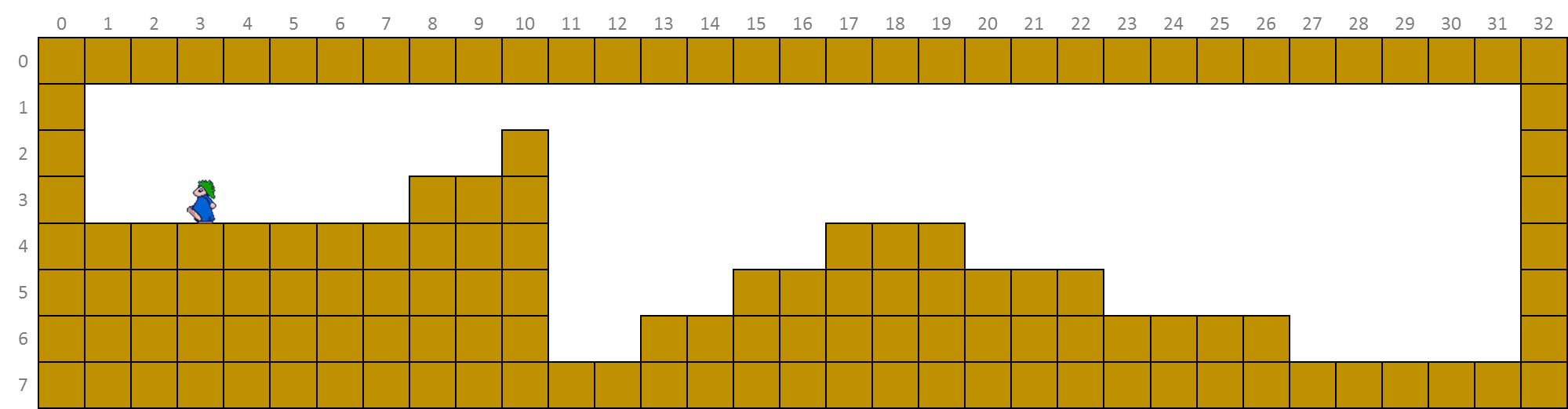
During each simulation step the lemming autonomously moves in a certain direction. Suppose the lemming wants to move to the right, there are three possible options that are illustrated in the figure below.

We call the cell where the lemming is currently located the current cell. If the cell to the right of the current cell is free (as in the left figure above), the lemmings moves to this cell. Then, the lemming falls down until it hits solid ground (if that was not already the case). If the cell to the right of the current cell contains an obstacle but the cell above the obstacle is free (as in the middle figure above), the lemming moves to that free cell. If both cells to the right and to upper right of the current cell contain an obstacle, the lemming stays in the current cell but now starts moving to the left. The lemming behaves in the same way if it wants to move to the left during the next step of the simulation.
You are asked to define a class Lemming that can be used to simulate a lemming in a given level of the video game Lemmings. This class must support at least the following methods:
An initialization method that takes three arguments: i) the location of a text file containing a description of the level, ii) the column where the lemming is initially dropped into the level through a trap door opening from above and iii) the direction in which the lemming initially wants to move. The direction is indicated by a less than symbol (<) if the lemming initially wants to move to the left and by a greater than symbol (>) if the lemming initially wants to move to the right. After execution of the initialization method, the lemming must always have solid ground under his feet.
A method position that returns a tuple of three elements: i) row index of the cell where the lemming is currently located, ii) column index of the cell where the lemming is currently located and iii) direction in which the lemming currently moves, indicated by a less than or a greater than symbol (same meaning as for the initialization method).
A method step that can be used to simulate a single step of the lemming. The method must return a tuple containing the position and direction of the lemming after the step has been taken, where the tuple has the same format used for the return value of the method position.
A method steps that takes an integer $$n \in \mathbb{N}$$. The method must simulate $$n$$ steps of the lemming, and return a list containing the positions and directions of the lemming after each step has been taken. The position and direction of the lemming must be represented by a tuple that has the same format used for the return value of the method position.
In addition, it must be possible to use the built-in function print to generate a string representation of the current position and direction of the lemming in the level. This string representation must display the level in the same way as it is represented in the given text file. The position where the lemming is currently located must be represented by a less than symbol (<) if the lemming currently moves to the left and by a greater than symbol (>) if the lemming currently moves to the right.
Example
In the following interactive session, we assume that the text file level.txt8 is located in the current directory.
>>> lemming = Lemming('level.txt', 3, '<')
>>> lemming.position()
(3, 3, '<')
>>> print(lemming)
#################################
# #
# # #
# < ### #
########### ### #
########### ######## #
########### ############## #
#################################
>>> lemming.step()
(3, 2, '<')
>>> lemming.step()
(3, 1, '<')
>>> lemming.step()
(3, 1, '>')
>>> lemming.step()
(3, 2, '>')
>>> print(lemming)
#################################
# #
# # #
# > ### #
########### ### #
########### ######## #
########### ############## #
#################################
>>> lemming.steps(5)
[(3, 3, '>'), (3, 4, '>'), (3, 5, '>'), (3, 6, '>'), (3, 7, '>')]
>>> print(lemming)
#################################
# #
# # #
# >### #
########### ### #
########### ######## #
########### ############## #
#################################
>>> lemming.step()
(2, 8, '>')
>>> print(lemming)
#################################
# #
# > # #
# ### #
########### ### #
########### ######## #
########### ############## #
#################################
>>> lemming.step()
(2, 9, '>')
>>> lemming.step()
(1, 10, '>')
>>> print(lemming)
#################################
# > #
# # #
# ### #
########### ### #
########### ######## #
########### ############## #
#################################
>>> lemming.step()
(6, 11, '>')
>>> print(lemming)
#################################
# #
# # #
# ### #
########### ### #
########### ######## #
###########> ############## #
#################################
>>> lemming.steps(21)
[(6, 12, '>'), (5, 13, '>'), (5, 14, '>'), (4, 15, '>'), (4, 16, '>'), (3, 17, '>'), (3, 18, '>'), (3, 19, '>'), (4, 20, '>'), (4, 21, '>'), (4, 22, '>'), (5, 23, '>'), (5, 24, '>'), (5, 25, '>'), (5, 26, '>'), (6, 27, '>'), (6, 28, '>'), (6, 29, '>'), (6, 30, '>'), (6, 31, '>'), (6, 31, '<')]
>>> lemming.steps(21)
[(6, 30, '<'), (6, 29, '<'), (6, 28, '<'), (6, 27, '<'), (5, 26, '<'), (5, 25, '<'), (5, 24, '<'), (5, 23, '<'), (4, 22, '<'), (4, 21, '<'), (4, 20, '<'), (3, 19, '<'), (3, 18, '<'), (3, 17, '<'), (4, 16, '<'), (4, 15, '<'), (5, 14, '<'), (5, 13, '<'), (6, 12, '<'), (6, 11, '<'), (6, 11, '>')]
>>> print(lemming)
#################################
# #
# # #
# ### #
########### ### #
########### ######## #
###########> ############## #
#################################The following animation simulates a sequence of steps the lemming makes in the level from the above example, and makes use of the string representation that should also be displayed by the built-in function print. We also have made explicit animations of the lemming falling down until it hits solid ground, but it should be taken into account that these movements are not separate steps of the simulation.