Een ellips¹ is een speciale vlakke kromme die men soms ook ovaal noemt. Een ellips heeft een vergelijking van de vorm:

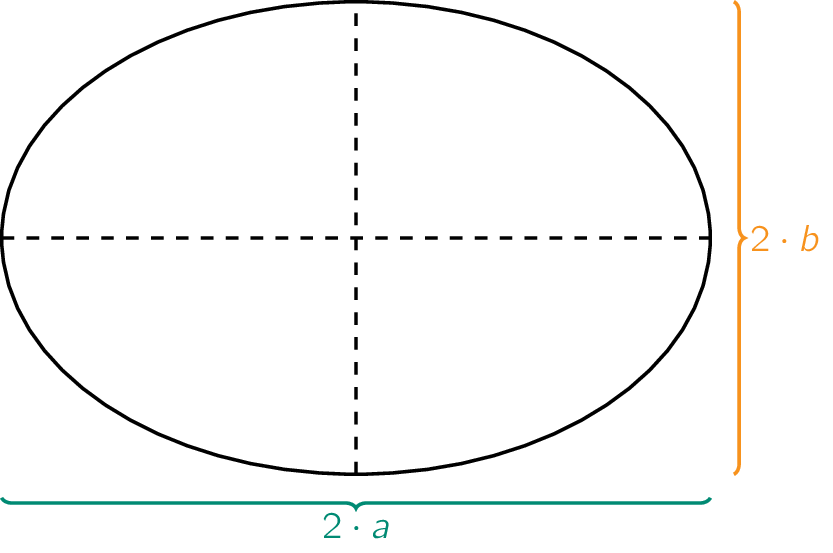
\[\mathsf{\dfrac{x^2}{a} + \dfrac{y^2}{b} = 1}\]

Hierbij stellen \(\mathsf{2\cdot a}\) en \(\mathsf{2\cdot b}\) respectievelijk de lange en korte as voor, zoals in onderstaande figuur weergegeven.

Het wiskundige genie Ramanujan² bepaalde in 1914 onderstaande formule als benadering voor de omtrek \(\mathsf{P}\) van een ellips.

\[\mathsf{P \approx \pi \cdot (a+b) \cdot \left(1+ \dfrac{3h}{10 + \sqrt{4-3h}}\right) \qquad \text{met} \qquad h = \dfrac{(a-b)^2}{(a+b)^2}}\]

Opgave

Schrijf een programma dat achtereenvolgens de lengte van de lange as en korte as vraagt en vervolgens de omtrek via bovenstaande formule benadert. Rond de omtrek af op 2 cijfers na de komma.

Voorbeeld

Voor een ellips met een lange as van 6.4 cm en een korte as van 4.0 cm verschijnt er:

De omtrek van de ellips meet bij benadering: 16.55 cm.