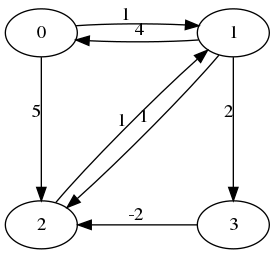
Gegeven is een graaf \((V,E)\) met toppen \(V\) en gerichte, gewogen bogen \(E\). We zoeken hierin het kortste pad van een gegeven starttop naar een gegeven bestemming.

Het algoritme van Dijkstra gaat er van uit dat alle gewichten positief zijn. Indien er ook negatieve gewichten voorkomen, garandeert de gretige aanpak van Dijkstra immers niet dat het correcte kortste pad gevonden wordt. Het algoritme van Bellman-Ford is een variant van het algoritme van Dijkstra die wel met negatieve gewichten omkan. De prijs die daarvoor betaald wordt, is een verhoogde tijdscomplexiteit.

In een graaf met sommige negatieve gewichten kan er eventueel een negatieve cykel voorkomen, d.w.z. een cykel waarvan de som van de gewichten van de bevatte bogen negatief is. Indien zo’n cykel bereikbaar is vanuit de starttop, is het kortste pad ongedefinieerd. We kunnen immers het totale gewicht van elk pad dat deze cykel bevat arbitrair klein maken door herhaaldelijk de cykel te doorlopen. Het algoritme van Bellman-Ford kan dergelijke negatieve cykels ook detecteren en geeft dan een gepaste foutmelding.

Net zoals inhet algoritme van Dijkstra, wordt de afstand van de starttop tot elke andere top benaderd en iteratief bijgestuurd tot ze convergeert naar de effectieve kortste afstand. Het bijsturen gebeurt hier bovendien ook via hetzelfde mechanisme: we nemen een boog \((u,v)\) en kijken of we een kortere weg naar \(v\) gevonden hebben door via \(u\) te gaan. Bij Dijkstra worden stap voor stap alle uitgaande bogen verwerkt van de tot dan toe nog niet bezochte top met minimale afstand (gretig). Elke boog wordt dus slechts eenmaal bekeken. Dit is echter niet voldoende wanneer er negatieve gewichten voorkomen.

In het algoritme van Bellman-Ford worden de updates \(\lvert V \lvert -1\) keer toegepast voor alle bogen (in arbitraire volgorde). Na de \(i\)-de update, hebben we zo reeds alle kortste paden gevonden bestaande uit hoogstens \(i\) bogen. Aangezien elk mogelijk pad zonder cykel hoogstens \(\lvert V \lvert -1\) bogen bevat, moeten we dus precies zoveel keer alles updaten om zeker te zijn dat het kortste pad gevonden is. Vervolgens updaten we nog een laatste keer en als dit resulteert in enige wijziging, hebben we een negatieve cykel gevonden (denk erover na waarom dit zo is).

De pseudocode ziet er als volgt uit:

function BellmanFord(graph, source, destination)
   
   distance = []
   predecessor = []

   // stap 1: initialisatie
   for each vertex v in graph.vertices:
      predecessor[v] = null
      if v is source:
         distance[v] = 0
      else:
         distance[v] = inf

   // stap 2: herhaaldelijk updaten
   for i from 1 to size(graph.vertices)-1:
      for each edge (u,v) in graph.edges:
         w = edge.weight
         if distance[u] + w < distance[v]:
            distance[v] = distance[u] + w
            predecessor[v] = u

   // stap 3: check negatieve cykel
   for each edge (u,v) in graph.edges:
      w = edge.weight
      if distance[u] + w < distance[v]:
         error "Graaf bevat een negatieve cykel"
           
   // stap 4: reconstrueer korste pad
   vertex = destination
   path = [destination]
   while vertex != source:
      vertex = predecessor[vertex]
      if vertex == null:
         error "Bestemming onbereikbaar uit starttop"
      path = [vertex, path]
   		
   return path

Opgave

Implementeer dit algoritme in een Python-functie bellman_ford(graph: dict, source, destination). Deze functie krijgt een gewogen adjacentielijst, een source en een destination als input, en moet een kortste pad teruggeven van source naar destination. Indien er geen pad bestaat, of er een negatieve cykel in de graaf zit, moet een lege lijst teruggegeven worden.

Merk op

Het is mogelijk om de berekeningen soms vroegtijdig te stoppen. Denk er over na wanneer dit kan en voer de nodige wijzigingen door in het algoritme. Wat is de asymptotische tijdscomplexiteit van het originele en gewijzigde algoritme?

Voorbeeld

>>> bellman_ford({0: [(1, 1), (5, 2)], 1: [(4, 0), (1, 2), (2, 3)], 2: [(1, 1)], 3: [(-2, 2)]}, 0, 2)
[0, 1, 3, 2]