In 1872, Ludwig Boltzmann came up with an equation relating the entropy $$S$$ of a configuration to the amount of microstates that are compatible with the configuration. The relation is simple but of great importance: \[ S = k\ln(W) \] with $$W$$ is the amount of microstates, and $$\ln$$ is the natural logarithm. Only long after his death was he recognized as one of the pioneers of statistical physics. His equation is now carved onto his tombstone.

Assignment

In this assignment, we calculate the entropy of a 2D configuration of blocks having dimensions $$2 \times 1$$ (like domino tiles). These blocks could form a simple physics model, e.g. for diatomic molecules. We impose the following simplifying assumptions and constraints:

• blocks must fill the space completely (no gaps)

• the total height of our 2-dimensional box is 3

• blocks can be placed horizontally or vertically

If we now define the width of the 2-dimensional box as $$n$$ (and impose that it is even), we can calculate the amount of microstates (and thus the entropy, using $$S = k\ln(W)$$). One possible microstate for $$n = 12$$ is shown below.

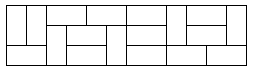
Your task:

• Write a function microstates that takes an even integer $$n \in \mathbb{N}$$. The function must return the number of different of microstates that completely fill a $$3 \times n$$ box. In case the given value is odd, the function must raise an AssertionError with the message argument must be even.

• Write a function entropy that takes an even integer $$n \in \mathbb{N}$$. The function must return the entropy of the configuration (under the assumptions described above, with $$k = 1$$). In case the given value is odd, the function must raise an AssertionError with the message argument must be even.

Example

>>> microstates(2)
3
>>> microstates(8)
153
>>> microstates(12)
2131

>>> entropy(2)
1.0986122886681098
>>> entropy(8)
5.030437921392435
>>> entropy(12)
7.664346632098617