Het niet-additieve meervoudig lineair regressiemodel
Interactie tussen continue variabele en factor variabele
We breiden het meervoudig lineaire regressie model nu uit door toevoeging van interactie-termen.
Het model in de vorige secties werd een additief model genoemd omdat de bijdrage van het kanker volume in lpsa niet afhangt van de hoogte van het prostaat gewicht en de status van de zaadblaasjes. De helling voor lcavol hangt m.a.w. niet af van de hoogte van het log prostaat gewicht en de status van de zaadblaasjes.
\[\beta_0 + \beta_v (x_{v}+\delta_v) + \beta_w x_{w} +\beta_s x_{s} - \beta_0 - \beta_v x_{v} - \beta_w x_{w} -\beta_s x_s = \beta_v \delta_v\]De svi status en de hoogte van het log-prostaatgewicht (\(x_w\)) heeft geen invloed op de bijdrage van het log-tumorvolume (\(x_v\)) in de gemiddelde log-prostaat antigeen concentratie en vice versa.
Het zou nu echter kunnen zijn dat de associatie tussen lpsa en lcavol, en tussen lpsa en log-prostaatgewicht wel afhangt van de status van de zaadblaasjes. De gemiddelde toename in lpsa tussen patiënten die één eenheid in het log-tumorvolume verschillen zou bijvoorbeeld lager kunnen zijn voor patiënten met een aangetaste zaadblaasjes dan bij patiënten waarvan de zaadblaasjes niet zijn aangetast. De associatie van het tumorvolume en de prostaat antigeen concentratie hangt in dit geval af van de status van de zaadblaasjes.
Om een dergelijke of tussen 2 variabelen \(X_v\) en \(X_s\) enerzijds en tussen \(X_w\) en \(X_s\) anderzijds statistisch te modelleren kan men producten van de variabelen in kwestie aan het model toevoegen:
\[Y_i = \beta_0 + \beta_v x_{iv} + \beta_w x_{iw} +\beta_s x_{is} + \beta_{vw} x_{iv}x_{is} + \beta_{vw} x_{iw}x_{is} +\epsilon_i\]Deze termen kwantificeren de interactie-effecten van respectievelijk de predictoren \(x_v\) en \(x_s\); en van \(x_w\) en \(x_s\) op de gemiddelde uitkomst. In dit model worden de termen \(\beta_vx_{iv}\), \(\beta_wx_{iw}\) en \(\beta_sx_{is}\) dikwijls de hoofdeffecten van de predictoren \(x_v\), \(x_w\) en \(x_s\) genoemd.
We schatten dit model nu in R. De interacties worden toegevoegd door een
term toe te voegen in de formule met de naam van twee variabelen die
wordt gescheiden door een :.
lmVWS_IntVS_WS <- lm(lpsa ~ lcavol + lweight + svi + svi:lcavol + svi:lweight,data=prostate)
summary(lmVWS_IntVS_WS)
##
## Call:
## lm(formula = lpsa ~ lcavol + lweight + svi + svi:lcavol + svi:lweight,
## data = prostate)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.50902 -0.44807 0.06455 0.45657 1.54354
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.52642 0.56793 -0.927 0.356422
## lcavol 0.54060 0.07821 6.912 6.38e-10 ***
## lweight 0.58292 0.15699 3.713 0.000353 ***
## sviinvasion 3.43653 1.93954 1.772 0.079771 .
## lcavol:sviinvasion 0.13467 0.25550 0.527 0.599410
## lweight:sviinvasion -0.82740 0.52224 -1.584 0.116592
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.7147 on 91 degrees of freedom
## Multiple R-squared: 0.6367, Adjusted R-squared: 0.6167
## F-statistic: 31.89 on 5 and 91 DF, p-value: < 2.2e-16
Het effect van lcavol op lpsa en het effect van lweight op lpsa zal nu afhangen van de waarde voor svi. \(X_s\) is echter een dummy variabele die twee waarden aan kan nemen, \(X_s=0\) als de zaadblaasjes niet aangetast zijn en \(X_s=1\) als er invasie is van de zaadblaadjes. Gezien \(X_S\) een dummy variabele is bekomen we nu twee verschillende regressievlakken:
- Een regressievlak voor \(X_s=0\):
waar de hellingen voor lcavol en lweight de hoofdeffecten zijn.
- En een regressievlak voor \(X_s=1\):
waar het intercept \(\beta_0 + \beta_s\) is, de som van het intercept en het hoofdeffect voor \(X_s\), en de hellingen voor lcavol en lweight respectievelijk \(\beta_v+\beta_{vs}\) en \(\beta_w+\beta_{ws}\) zijn, m.a.w. de sum van het hoofdeffect en de overeenkomstige interactieterm.
Grafisch wordt het model weergegeven in Figuur 63.
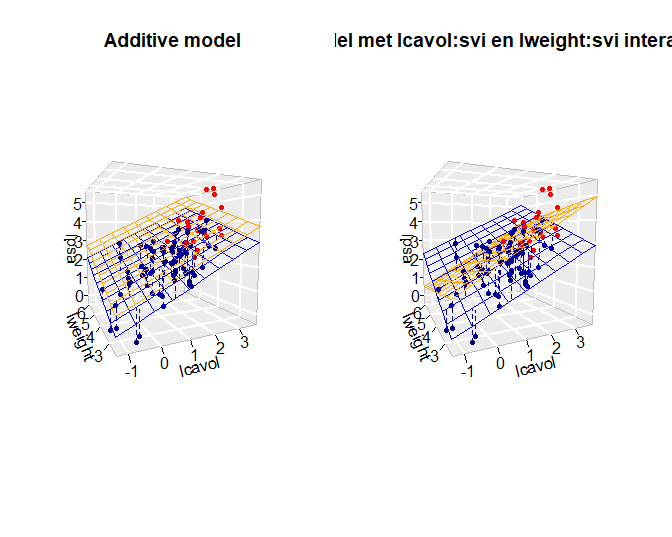
Figuur 63: Fit van het additieve model met de termen lcavol, lweight, svi (links) en het model met interacties lcavol, lweight, svi . lcavol:svi, lweight:svi (rechts). De rechtse figuur toont duidelijk dat de interactie er nu voor zorgt dat de associaties tussen de response \<-\> het log-tumorvolume en de response \<-\> het log-gewicht afhankelijk is van de status van de zaadblaasjes. De interacties zorgen voor andere hellingen bij patiënten met (rood) en zonder invasie (blauw) van de zaadblaasjes. Voor het additieve model (links) zien we enkel een verschuiving van het regressievlak, maar parallelle hellingen. Het hoofdeffect voor een factor variabele zorgt m.a.w. voor een ander intercept.
Merk op dat de helling voor lcavol groter is bij patiënten met invasie van de zaadblaasjes dan bij patiënten zonder invasie van de zaadblaasjes en dat de helling voor lweight van teken veranderd. We merken verder op dat beide interactie-termen opnieuw niet significant.