Theseus en de Minotaurus is een logische puzzel die bestaat uit een doolhof in de vorm van een rechthoekig rooster. Rondom het rooster staan muren en ook tussen aangrenzende vakjes kan er een muur staan die verhindert om van het ene naar het andere vakje te stappen. Als speler neem je de rol aan van Theseus — koning van Athena — die de uitgang van het doolhof moet zien te bereiken. Daarbij wordt Theseus opgejaagd door de Minotaurus, die twee stappen zet voor elke stap die Theseus zet. Dit is bijvoorbeeld de beginopstelling van de eerste puzzel, waarbij de positie van de uitgang wordt aangeduid door een wenteltrap, de positie van Theseus door een blauwe cirkel en de positie van de Minotaurus door een oranje cirkel.

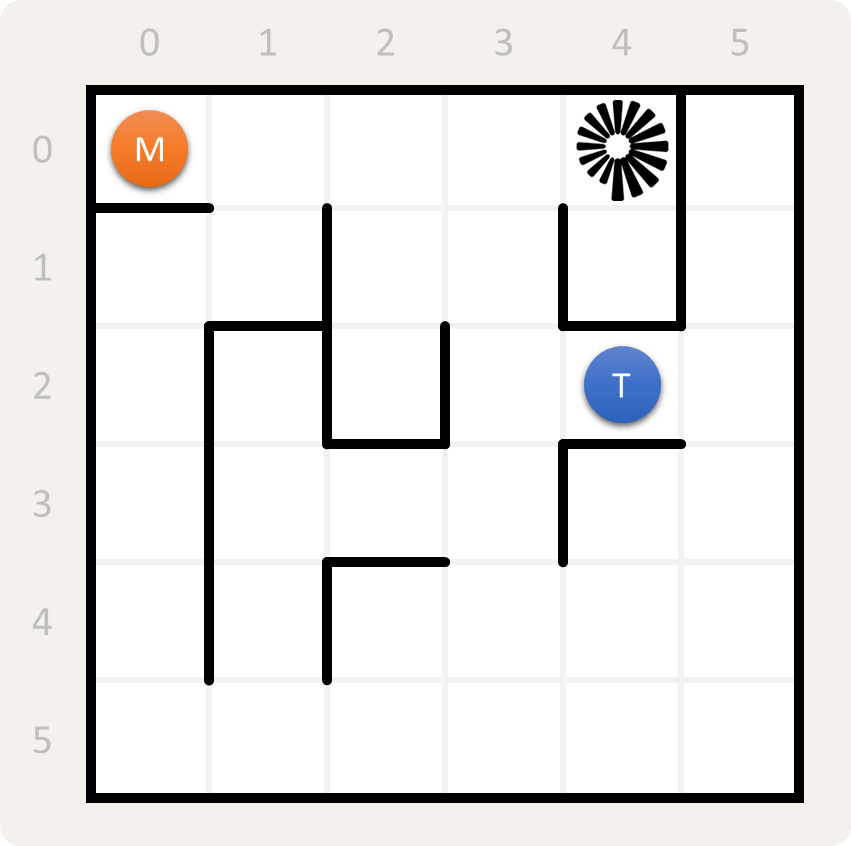
Hoewel de Minotaurus dus sneller is dan Theseus, zijn zijn beweging compleet voorspelbaar en vaak inefficiënt: ze worden bepaald door te kijken of hij dichter bij Theseus kan komen door horizontaal te bewegen, en vervolgens te kijken of hij dichter kan komen door verticaal te bewegen. Als geen van beide bewegingen hem dichter bij Theseus zou brengen, dan slaat de Minotaurus zijn beurt over. Ook Theseus mag zijn beurt overslaan.

Dit type doolhof werd voor het eerst gepubliceerd in 1990 in het boek Mad Mazes van Robert Abbott. Het idee werd later gepubliceerd in het Britse tijdschrift Games & Puzzles.

Opgave

Het $$m \times n$$ rooster van een doolhof uit Theseus en de Minotaurus bestaat uit $$m$$ rijen en $$n$$ kolommen. De rijen worden van boven naar onder genummerd, en de kolommen van links naar rechts, telkens vanaf nul. Daardoor kan de positie van een vakje in het rooster voorgesteld worden door een reeks $$[r, k]$$ (Array), waarbij $$r \in \mathbb{N}$$ (Number; $$0 \leq r < m$$) het nummer is van de rij en $$k \in \mathbb{N}$$ (Number; $$0 \leq k < n$$) het nummer van de kolom waarop het vakje zicht bevindt. Bij de beginopstelling van het $$6 \times 6$$ doolhof uit de inleiding bevindt de uitgang zich bijvoorbeeld op positie $$(0, 4)$$, Theseus op positie $$(2, 4)$$ en de Minotaurus op positie $$(0, 0)$$.

Als afstand tussen twee vakjes op posities $$(r_1, k_1)$$ en $$(r_2, k_2)$$ gebruiken we de Manhattan-afstand: \[ |r_1 - r_2| + |k_1 - k_2| \]

De $$(m + 1) \times n$$ posities waar er horizontale muren kunnen staan in het rooster worden rij per rij (van boven naar onder) van links naar rechts genummerd vanaf nul. Op alle posities langs de boven- en onderrand staan er horizontale muren die hieronder links aangeduid worden met oranje lijnen. De bijkomende horizontale muren worden voorgesteld door een reeks (Array) met nummers (Number) van posities waar er horizontale muren staan die zich niet op de rand van het rooster bevinden. Het doolhof uit de inleiding heeft bijvoorbeeld bijkomende horizontale muren op posities $$[6, 13, 16, 20, 22, 26]$$ die hieronder links aangeduid worden met groene lijnen.

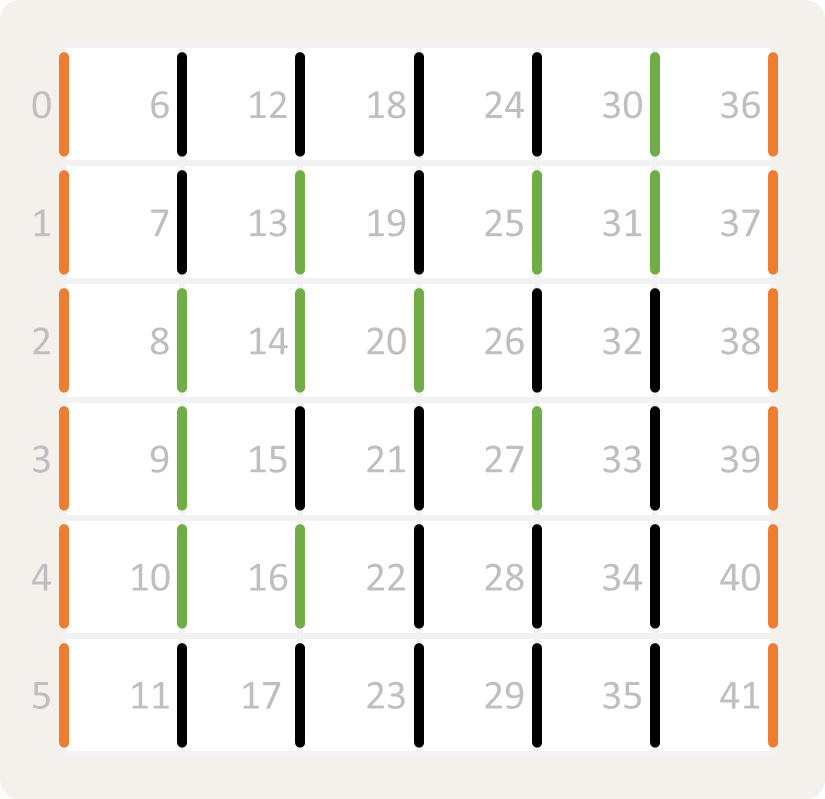
De $$m \times (n + 1)$$ posities waar er verticale muren kunnen staan in het rooster worden kolom per kolom (van links naar rechts) van boven naar onder genummerd vanaf nul. Op alle posities langs de linker en rechter rand staan er verticale muren die hierboven rechts aangeduid worden met oranje lijnen. De bijkomende verticale muren worden voorgesteld door een reeks (Array) met nummers (Number) van posities waar er verticale muren staan die zich niet op de rand van het rooster bevinden. Het doolhof uit de inleiding heeft bijvoorbeeld bijkomende verticale muren op posities $$[8, 9, 10, 13, 14, 16, 20, 25, 27, 30, 31]$$ die hierboven rechts aangeduid worden met groene lijnen.

De vier richtingen waarin Theseus en de Minotaurus zich kunnen verplaatsen, worden voorgesteld door een hoofdletter (String): L (naar links), R (naar rechts), U (naar boven) en D (naar onder). Het overslaan van een beurt wordt gezien als de vijfde richting waarin Theseus en de Minotaurus zich kunnen verplaatsen, die wordt voorgesteld door de hoofdletter P (String).

Definieer een klasse Doolhof waarmee het verloop van een spelletje Theseus en de Minotaurus kan gesimuleerd worden. Elk spel heeft een gegeven configuratie van het doolhof en een gegeven beginopstelling van Theseus en de Minotaurus. Bij het aanmaken van een nieuw spel (Doolhof) moeten er zeven argumenten doorgegeven worden: i) het aantal rijen $$m$$ van het rooster (Number; $$m \geq 3$$), ii) het aantal kolommen $$n$$ van het rooster (Number; $$n \geq 3$$), iii) de bijkomende horizontale muren, iv) de bijkomende verticale muren, v) de positie van de uitgang, vi) de beginpositie van Theseus en vii) de beginpositie van de Minotaurus. Een spel (Doolhof) minstens ook de volgende methoden ondersteunen:

• Een methode isGeldig waaraan drie argumenten moeten doorgegeven worden: i) een rijnummer $$r$$ (Number), ii) een kolomnummer $$k$$ (Number) en iii) een letter $$d$$ (String). De methode moet een Booleaanse waarde (Boolean) teruggeven, die aangeeft of men zich vanaf positie $$[r, k]$$ naar een aangrenzend vakje in richting $$d$$ zou kunnen verplaatsen. Dat is het geval als i) het vakje op positie $$(r, k)$$ binnen het rooster ligt, ii) letter $$d$$ een richting aanduidt (L, R, U, D of P) en iii) men bij een verplaatsing vanaf positie $$(r, k)$$ in richting $$d$$ niet tegen een muur botst.

• Een methode toString waaraan geen argumenten moeten doorgegeven worden. De methode moet een stringvoorstelling (String) van het doolhof teruggegeven met de huidige positie van Theseus en de huidige positie van de Minotaurus. Het exacte formaat van de stringvoorstelling kan je afleiden uit onderstaand voorbeeld. De snijpunten van rijen en kolommen waarop muren kunnen staan, worden voorgesteld door plustekens (+). Een positie waarop een horizontale muur staat wordt voorgesteld door een koppelteken (-) en een positie waar geen horizontale muur staat door een spatie. Een positie waarop een verticale muur staat wordt voorgesteld door een verticale streep (|) en een positie waar geen verticale muur staat door een spatie. De positie van de uitgang wordt aangeduid met hoofdletter S, de huidige positie van Theseus met hoofdletter T en de huidige positie van de Minotaurus met hoofdletter M. Als twee of drie van deze items op dezelfde positie staan, dan gebruiken we de hoofdletter van het laatste item uit voorgaande zin. Posities waarop geen enkel item staat worden voorgesteld met een spatie.

• Een methode verzetTheseus waaraan een letter $$d$$ (String) moet doorgegeven worden. De methode moet ervoor zorgen dat Theseus zich vanaf zijn huidige positie verplaatst naar het aangrenzend vakje in richting $$d$$ (L, R, U, D of P). Als dit geen geldige verplaatsing is, dan moet Theseus blijven staan en moet er een Error opgeworpen worden met de boodschap ongeldige zet.

• Een methode verzetMinotaurus waaraan geen argumenten moeten doorgegeven worden. De methode moet ervoor zorgen dat de Minotaurus zich vanaf zijn huidige positie verplaatst naar een aangrenzend vakje volgens een vast algoritme. Als er een geldige horizontale verplaatsing (naar links (L) of rechts (R)) is die de Manhattan-afstand tussen de Minotaurus en Theseus kleiner maakt, dan is dit de richting waarin de Minotaurus zich verplaatst. Anders, als er een geldige verticale verplaatsing (naar boven (U) of onder (D)) is die de Manhattan-afstand tussen de Minotaurus en Theseus kleiner maakt, dan is dit de richting waarin de Minotaurus zich verplaatst. Anders blijft de Minotaurus gewoon staan (P). De methode moet de richting (String) teruggeven waarin de Minotaurus zich verplaatst — of P als de Minotaurus blijft staan.

• Een methode isGewonnen waaraan geen argumenten moeten doorgegeven worden. De methode moet een Booleaanse waarde (Boolean) teruggeven die aangeeft of Theseus het spel gewonnen heeft. Dat is het geval als Theseus zich op dezelfde positie bevindt als de uitgang.

• Een methode isVerloren waaraan geen argumenten moeten doorgegeven worden. De methode moet een Booleaanse waarde (Boolean) teruggeven die aangeeft of Theseus het spel verloren heeft. Dat is het geval als Theseus zich op dezelfde positie bevindt als de Minotaurus.

• Een methode verzet waaraan een string (String) moet doorgegeven worden. Voor elke letter $$d$$ in de gegeven string moet

  1. Theseus zich vanaf zijn huidige positie verplaatsen naar het aangrenzend vakje in richting $$d$$ (L, R, U, D of P); als dit geen geldige verplaatsing is, dan moet Theseus blijven staan en moet er een Error opgeworpen worden met de boodschap ongeldige zet

  2. de Minotaurus zich vanaf zijn huidige positie verplaatsen naar een aangrenzend vakje op basis van het vaste algoritme waarmee de Minotaurus zich verplaatst; de Minotaurus verplaatst zich enkel als Theseus het spel nog niet gewonnen of verloren heeft

  3. de vorige stap nog een keer herhaald worden

  De methode moet een string (String) teruggeven met hoofdletters die de opeenvolgende richtingen (L, R, U, D of P) aangegeven waarin de Minotaurus zich verplaatst heeft als reactie op de verplaatsingen van Theseus.

Voorbeeld

> const doolhof = new Doolhof(6, 6, [6, 13, 16, 20, 22, 26], [8, 9, 10, 13, 14, 16, 20, 25, 27, 30, 31], [0, 4], [2, 4], [0, 0]);
> doolhof.isGeldig(3, 4, "U")
false
> doolhof.isGeldig(3, 4, "D")
true
> doolhof.isGeldig(3, 4, "L")
false
> doolhof.isGeldig(3, 4, "R")
true
> console.log(doolhof.toString())
+-+-+-+-+-+-+
|M       S| |
+-+ + + + + +
|   |   | | |
+ +-+ + +-+ +
| | | |  T  |
+ + +-+ +-+ +
| |     |   |
+ + +-+ + + +
| | |       |
+ + + + + + +
|           |
+-+-+-+-+-+-+
> doolhof.verzetTheseus("U")
Error: ongeldige zet
> doolhof.verzetTheseus("R")
> console.log(doolhof.toString())
+-+-+-+-+-+-+
|M       S| |
+-+ + + + + +
|   |   | | |
+ +-+ + +-+ +
| | | |    T|
+ + +-+ +-+ +
| |     |   |
+ + +-+ + + +
| | |       |
+ + + + + + +
|           |
+-+-+-+-+-+-+
> doolhof.isGewonnen()
false
> doolhof.isVerloren()
false
> doolhof.verzetMinotaurus()
"R"
> console.log(doolhof.toString())
+-+-+-+-+-+-+
|  M     S| |
+-+ + + + + +
|   |   | | |
+ +-+ + +-+ +
| | | |    T|
+ + +-+ +-+ +
| |     |   |
+ + +-+ + + +
| | |       |
+ + + + + + +
|           |
+-+-+-+-+-+-+
> doolhof.verzetMinotaurus()
"R"
> console.log(doolhof.toString())
+-+-+-+-+-+-+
|    M   S| |
+-+ + + + + +
|   |   | | |
+ +-+ + +-+ +
| | | |    T|
+ + +-+ +-+ +
| |     |   |
+ + +-+ + + +
| | |       |
+ + + + + + +
|           |
+-+-+-+-+-+-+
> doolhof.verzet("D")
"RR"
> console.log(doolhof.toString())
+-+-+-+-+-+-+
|        M| |
+-+ + + + + +
|   |   | | |
+ +-+ + +-+ +
| | | |     |
+ + +-+ +-+ +
| |     |  T|
+ + +-+ + + +
| | |       |
+ + + + + + +
|           |
+-+-+-+-+-+-+
> doolhof.verzet("L")
"DP"
> console.log(doolhof.toString())
+-+-+-+-+-+-+
|        S| |
+-+ + + + + +
|   |   |M| |
+ +-+ + +-+ +
| | | |     |
+ + +-+ +-+ +
| |     |T  |
+ + +-+ + + +
| | |       |
+ + + + + + +
|           |
+-+-+-+-+-+-+
> doolhof.verzet("DLLDLLUUUURUDLDDDDRRRUUUUUR")
"PPPPPPPPPPPPPPPPPPPPPPULLLLPPPPPPPPPRDPPPPPPPPPPPPUR"
> console.log(doolhof.toString())
+-+-+-+-+-+-+
|    M   T| |
+-+ + + + + +
|   |   | | |
+ +-+ + +-+ +
| | | |     |
+ + +-+ +-+ +
| |     |   |
+ + +-+ + + +
| | |       |
+ + + + + + +
|           |
+-+-+-+-+-+-+
> doolhof.isGewonnen()
true