The Racetrack Playa is a scenic dry lake that is located above the northwestern side of Death Valley, in Death Valley National Park, California, U.S.. The playa is exceptionally flat and level, elevates 1132 m above sea level, with the northern end being only 4 cm higher than the southern end. During periods of heavy rain, water washes down from the Racetrack mountain area draining into the playa, forming a shallow, short-lived endorheic lake. Under the desert sun, the thin veneer of water quickly evaporates, leaving behind a surface layer of soft slick mud. As the mud dries, it shrinks and cracks into a mosaic pattern of interlocking polygons.
The lake is famous for a mysterious geological phenomenon of "sailing stones" that move and inscribe long tracks along the smooth valley floor without human or animal intervention. Stones with rough bottoms leave straight striated tracks, while those with smooth bottoms tend to wander. Stones sometimes turn over, exposing another edge to the ground and leaving a different track in the stone's wake. Trails differ in both direction and length. Rocks that start next to each other may travel parallel for a time, before one abruptly changes direction to the left, right, or even back to the direction from which it came. Trail length also varies – two similarly sized and shaped rocks may travel uniformly, then one could move ahead or stop in its track.

The phenomenon of rock motion has excited considerable interest, and there is scientific and popular literature extending back to the first report in 1948. Initial studies showed that the rocks move once every two or three years and that their traces usually remain visible for three to four years. Over time, many theories and hypotheses about the movement mechanism have been put forward. Rock movement has been variously attributed to high winds (over 145 kilometers per hour), liquid water, ice or ice flotation, but no one had observed the rock motion in action.
During the 2013-2014 winter, geologists from the Scripps Institute of Oceanography1 finally succeeded to observe rock movements using GPS and time-lapse photography2. The research team witnessed and documented rock movement on December 20, 2013, that involved more than 60 rocks, with some rocks moving up to 224 m between December 2013 and January 2014 in multiple move events. These observations contradicted earlier hypotheses of winds or thick ice floating rocks off the surface. Instead, rocks move when large ice sheets a few millimeters thick floating in an ephemeral winter pond start to break up during sunny days. These thin floating ice panels, frozen during cold winter nights, are driven by light winds and shove rocks at up to 5 m/min (0.3 km/h). Some GPS-measured moves lasted up to 16 minutes, and a number of stones moved more than five times during the existence of the playa pond in the winter of 2013-14. How massive rocks of hundreds of kilograms move and why some trails are missing rocks at the end of the track remains a mystery.
Assignment
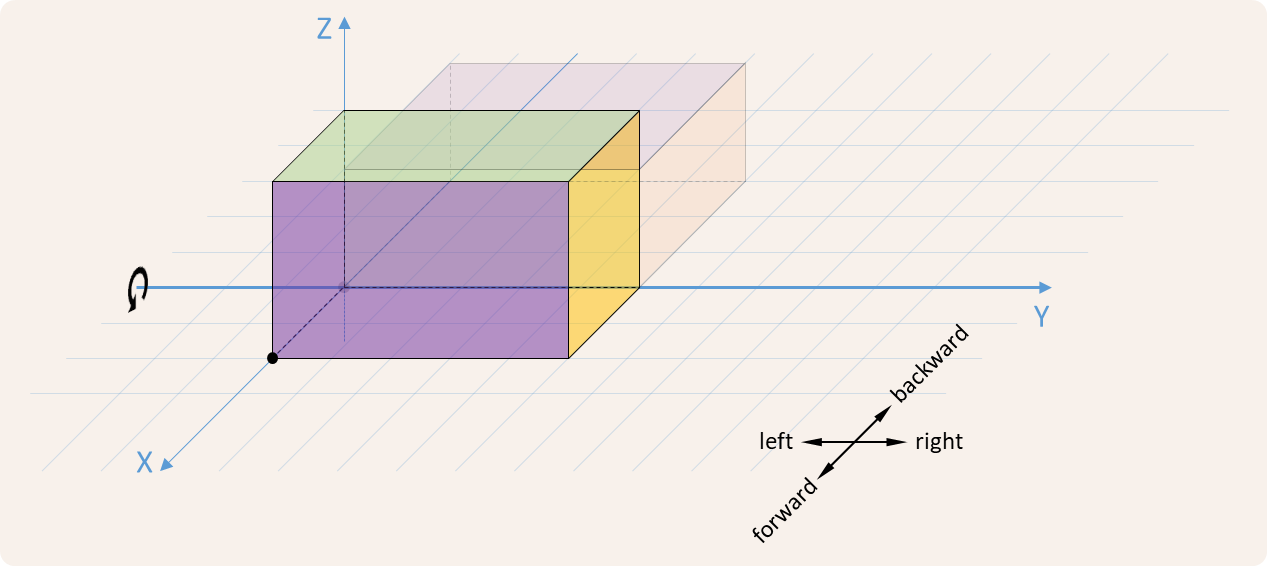
We represent a rock as a cuboid block that always sits on the base plane
(XY-plane) of a three-dimensional space with a fixed coordinate system, as
shown in the figure below. The rock is always viewed from a vantage point
along the positive X-axis in the direction of the YZ-plane. The front face
of the rock is always parallel to the YZ-plane. The dimensions of the rock
are described by its width
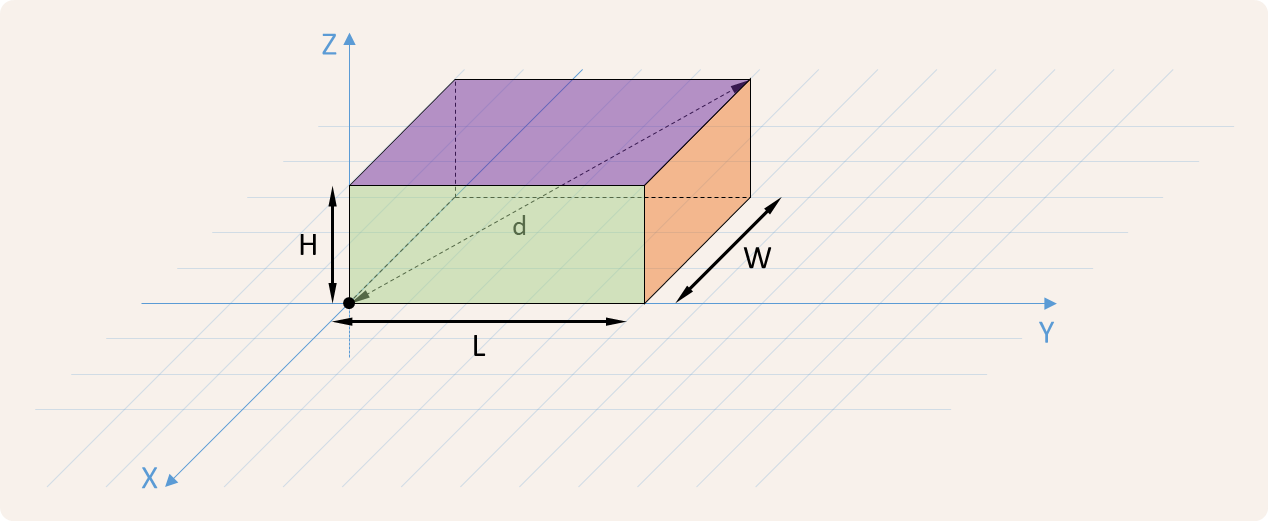
The area
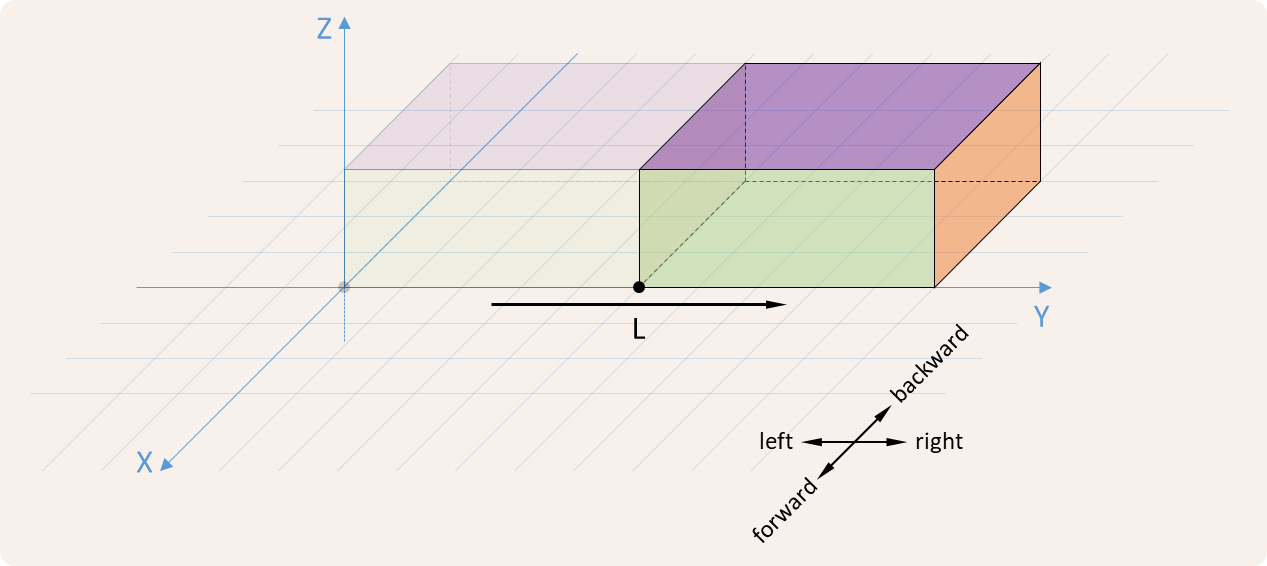
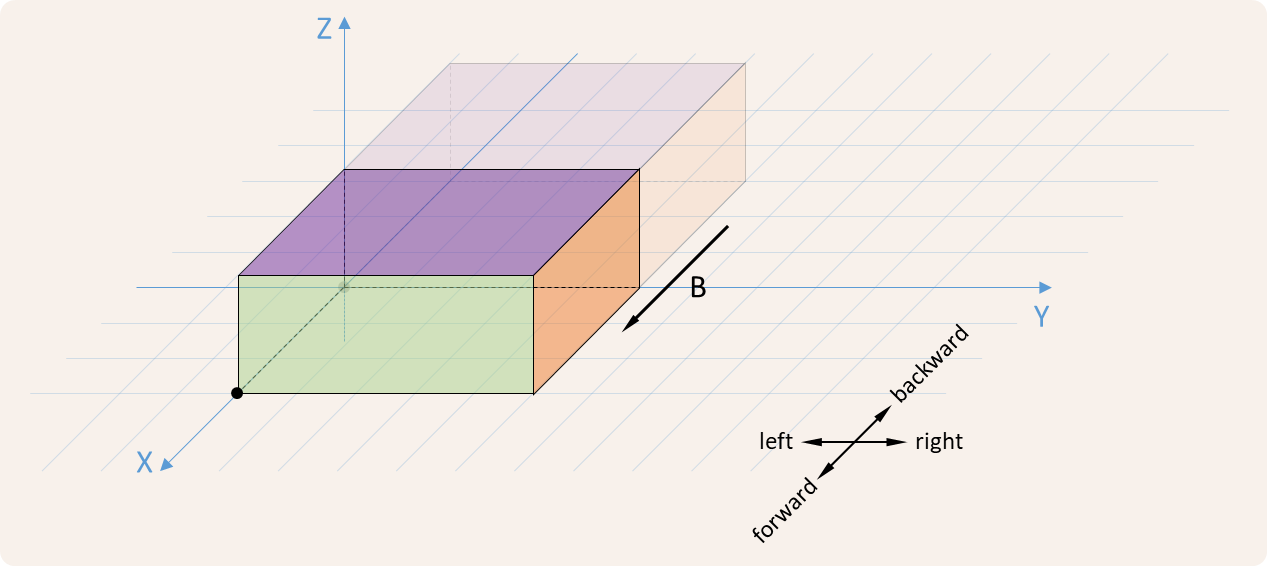
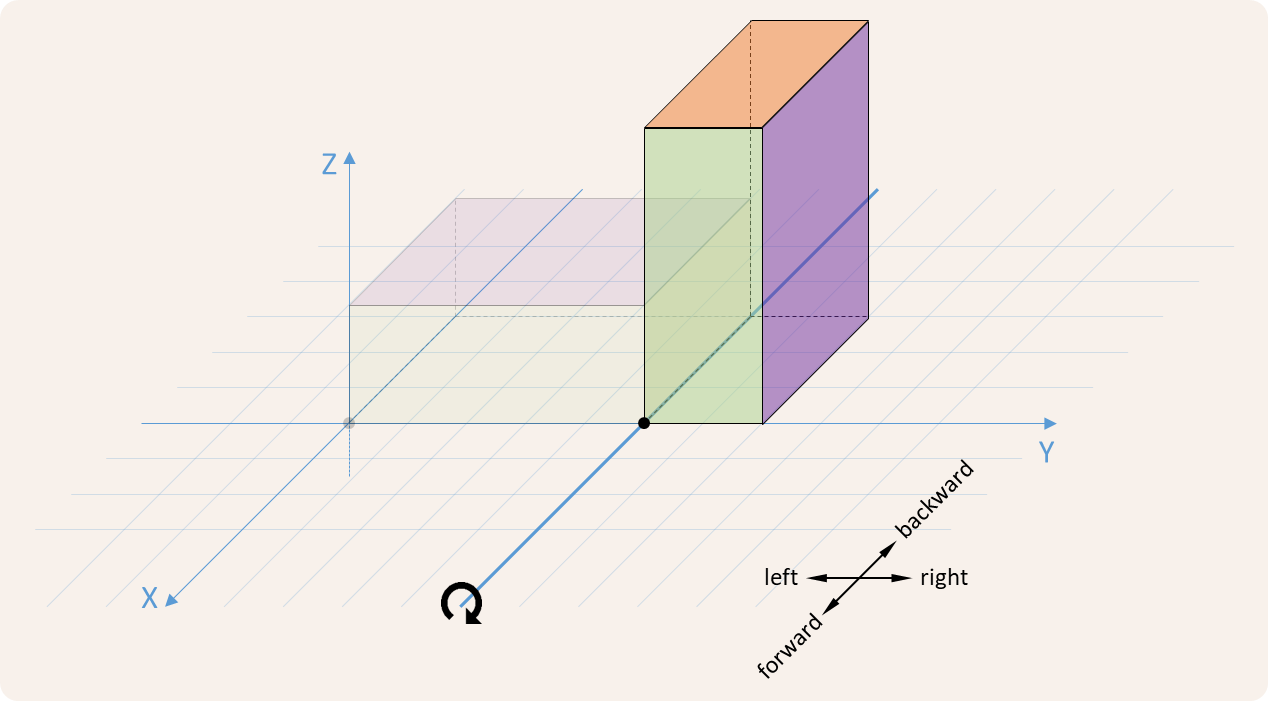
The rock may also tilt to the left, to the right, forward or backward. This is illustrated in the figures below.
Define a class Block to represent rocks that have
dimensions and a position as described above, and that can move in the two
ways specified. When creating a new rock (Block), integers (int)
must be passed to the three parameters length, height,
and width, which respectively specify the length, the height
and the width of the rock. There is also an optional fourth parameter position
to which a sequence (list or tuple) of two
integers (int) can be passed, specifying the position of the
bottom-left vertex in the front face of the rock. If no value is
explicitly passed to the position parameter, this vertex
lies in the origin
When a rock
On a rock
-
A method area that takes no arguments. The method must return the surface area (float) of rock
-
A method volume that takes no arguments. The method must return the volume (float) of rock
-
A method diagonal that takes no arguments. The method must return the length (float) of the space diagonal of rock
-
A method slide that takes a string (str) consisting of a single letter. This letter indicates the direction in which rock
-
A method tilt that takes a string (str) consisting of a single letter. This letter indicates the direction in which rock
-
A method sail that takes a string (str) with an even length. The string must alternately consist of letters indicating a particular movement (S for slide or T for tilt) and letters indicating a particular direction (L for left, R for right, F for forward and B for backward). For example, SB stands for slide backward, TR for tilt to the right, and SBTR for first slide backward and then tilt to the right. If a character at an even position in the string does not match any of the uppercase letters representing movements, then rock
Example
>>> rock = Block(5, 2, 3) >>> rock Block(length=5, height=2, width=3, position=(0, 0)) >>> rock.area() 62.0 >>> rock.volume() 30.0 >>> rock.diagonal() 6.164414002968976 >>> rock2 = rock.slide('R') >>> rock2 Block(length=5, height=2, width=3, position=(0, 5)) >>> rock is rock2 True >>> rock.slide('F') Block(length=5, height=2, width=3, position=(3, 5)) >>> rock.tilt('L') Block(length=2, height=5, width=3, position=(3, 3)) >>> rock.tilt('B') Block(length=2, height=3, width=5, position=(0, 3)) >>> rock.tilt('B').slide('L').tilt('L').slide('B') Block(length=5, height=2, width=3, position=(-8, -4)) >>> rock.sail('SB') Block(length=5, height=2, width=3, position=(-11, -4)) >>> rock.sail('TR') Block(length=2, height=5, width=3, position=(-11, 1)) >>> rock.sail('SFSFTLSLTBTBSRSFTRTFTRTRSBSF') Block(length=2, height=3, width=5, position=(-2, 6)) >>> rock.tilt('X') Traceback (most recent call last): AssertionError: invalid direction >>> rock.sail('XY') Traceback (most recent call last): AssertionError: invalid movement >>> rock.sail('TY') Traceback (most recent call last): AssertionError: invalid direction
Epilogue
Something significant happened on February 29, 1912 in Tandil, Argentina. A 300-ton stone that had perched impossibly on the edge of a local hill suddenly tumbled to the bottom and broke into pieces. Whether this happened due to vandalism or to blasting at a local quarry is unknown — there were no witnesses.

In 2007 the town replaced it with an exact replica. To date, it's still there.
Resources
-
Norris RD, Norris JM, Lorenz RD, Ray J, Jackson B (2014). Sliding rocks on Racetrack Playa, Death Valley National Park: first observation of rocks in motion. PloS one 9(8), e105948. 3
-
Lorenz RD, Jackson BK, Barnes JW, Spitale J, Keller JM (2011). Ice rafts not sails: Floating the rocks at Racetrack Playa. American Journal of Physics 79(1), 37-42. 4