Hermit is a strategy game for two players. It is played on a board with $$n \times n$$ squares, arranged in a square grid with $$n$$ rows and $$n$$ columns. At the start of the game, the board is empty. Off the board is a supply of three dimensional blocks with dimensions of $$1 \times 1 \times 2$$ units, where a unit is about the same length as the side of a square on the board. The blocks have three different colors: red, yellow and blue.

This Hermit game board has 16 squares arranged in a square $$4 \times 4$$ grid with 4 rows and 4 columns. Both players already placed some blocks on the board and off the board is a supply of some more blocks they can place on the board. The yellow circles indicate that there are only two possibilities left to place another block in this configuration of the board: a yellow block that is placed upright at one of the two empty squares touching the left border of the grid.

Schematic representation of a $$4 \times 4$$ Hermit board. At the start of the game, the board is empty as indicated by the white colored squares.

Each player in turn chooses a block of any color and places it either upright on the board so that it covers just one square, or on its side so that it covers two adjacent squares.

The colored three dimensional blocks can be placed upright on the board so that they cover just one square (left). They can also be placed horizontally (central) or vertically (right) or on their side so that they cover two adjacent squares.

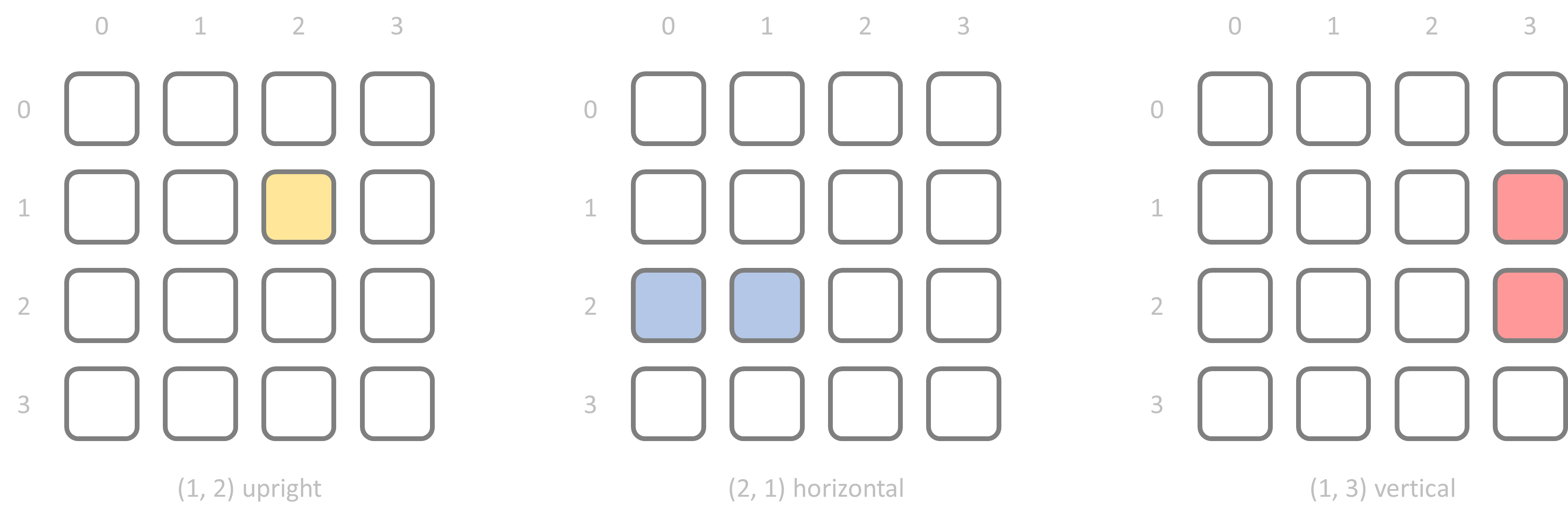
Blocks may only be placed on empty squares and can not touch a block of the same color, not even diagonally. The configuration in the diagram below has its blocks positioned as in the above picture. Yellow circles indicate the only two possibilities to place another block: a yellow block that is placed upright at position $$(1, 0)$$ or at position $$(3, 0)$$.

The two yellow circles indicate the only two possibilities to place another block in this configuration of the board: a yellow block that is placed upright at position $$(1, 0)$$ or at position $$(3, 0)$$.

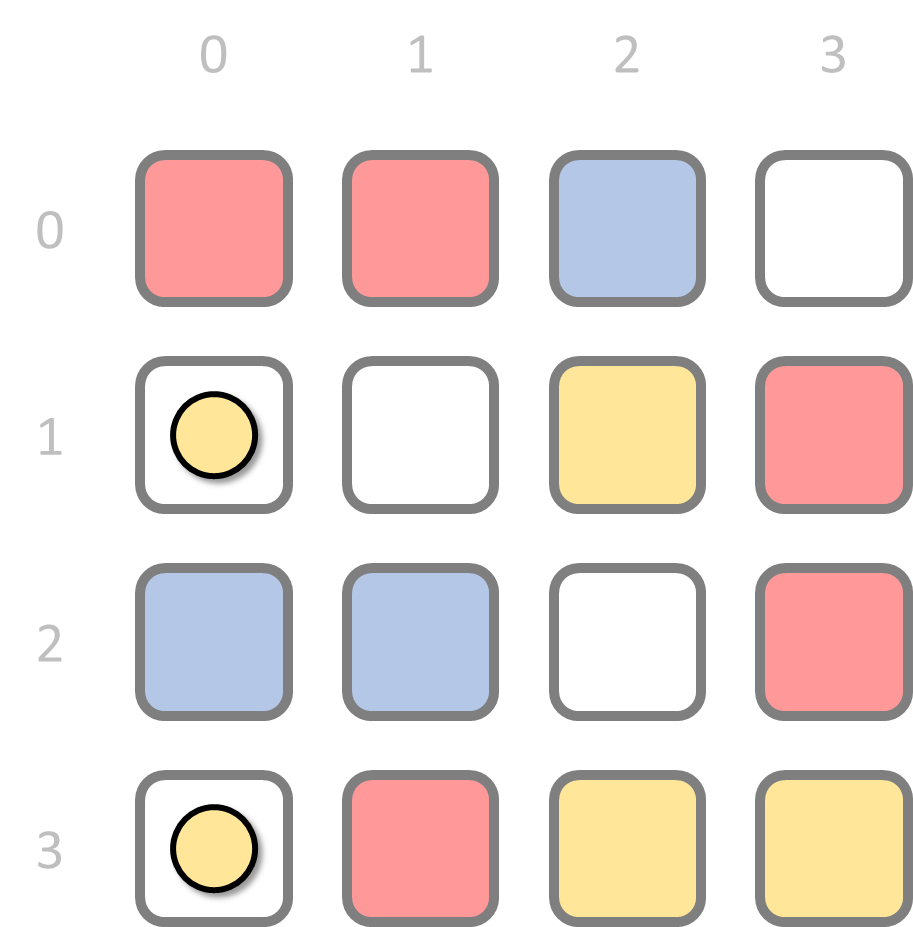
The first player who is unable to put another block on the board loses the game. Ties are not possible.

Assignment

To refer to the squares on a Hermit board, we number the rows from top to bottom and the columns from left to right, starting from zero. The position of a square on the board is then indicated by a tuple $$(r, c)$$, where $$r \in \mathbb{N}$$ (int) is the row number and $$c \in \mathbb{N}$$ (int) the column number.

The color of a block is indicated by an uppercase letter: Y (yellow), B (blue) or R (red).

The placement of a block is indicated by an uppercase letter: U (upright), H (horizontal) or V (vertical).

Define a class Hermit that can be used to simulate the progress of a Hermit game. The dimension $$n$$ (int) of the board must passed when creating a new game (Hermit). There are no blocks on the board at the start of the game.

If a game (Hermit) is passed to the built-in function str, a string representation (str) of the board must be returned in which each row of the board forms a separate line. Empty squares are represented as a dot (.) and squares covered by a block as the uppercase letter that indicates the color of the block. Representations of adjacent squares on the same row are separated from each other by a single space.

In addition, a game $$g$$ (Hermit) must at least support the following methods:

A method positions that takes two arguments: i) the position $$(r, c)$$ of a square on the board and ii) the placement $$P$$ (str) of a block. The method must return a set containing all positions that would be covered by a block with placement $$P$$ that has its top left corner at square $$(r, c)$$ on the board. A block that is placed upright only covers square $$(r, c)$$, a block that is placed horizontally covers squares $$(r, c)$$ and $$(r, c + 1)$$ and a block that is placed vertically covers squares $$(r, c)$$ and $$(r + 1, c)$$.

Note

Th method positions should not take into account the dimension of the game board: the set it returns may contain positions that lie outside the game board. The method should also not take into account other blocks that may have already been placed on the game board.
A method isvalid that takes two arguments: i) the color $$C$$ (str) of a block and ii) the position $$(r, c)$$ of a square on the board. The method must return a Boolean value (bool) that indicates whether position $$(r, c)$$ is an empty square within the board grid that does not touch another square of color $$C$$, not even diagonally.
A method move that takes three arguments: i) the color $$C$$ (str) of a block, ii) the position $$(r, c)$$ of a square on the board and iii) the placement $$P$$ (str) of a block. The method must place a block of color $$C$$ with its top left corner at square $$(r, c)$$ of the board and with placement $$P$$, and must return a reference to the game $$g$$ on which the method is called. If the block cannot be validly placed at the given position according to the rules of the game, no block may be placed and an AssertionError must be raised with message invalid move.
A method possible_moves that takes no arguments. The method must return a set containing all possibilities to put a block on the board during the next move. Such a possibility is represented as a tuple with three elements that correspond to the three arguments that are passed to the method move.

Example

        >>> board = Hermit(4)
>>> print(board)
. . . .
. . . .
. . . .
. . . .
>>> board.positions((0, 0), 'H')
{(0, 0), (0, 1)}
>>> board.isvalid('R', (0, 0))
True
>>> board.isvalid('R', (0, 1))
True
>>> print(board.move('R', (0, 0), 'H'))
R R . .
. . . .
. . . .
. . . .
>>> print(board.move('R', (1, 2), 'V'))
Traceback (most recent call last):
AssertionError: invalid move
>>> print(board.move('B', (0, 2), 'U').move('Y', (1, 2), 'U'))
R R B .
. . Y .
. . . .
. . . .
>>> print(board.move('R', (3, 1), 'U').move('Y', (3, 2), 'H'))
R R B .
. . Y .
. . . .
. R Y Y
>>> print(board.move('R', (1, 3), 'V').move('B', (2, 0), 'H'))
R R B .
. . Y R
B B . R
. R Y Y
>>> board.possible_moves()
{('Y', (1, 0), 'U'), ('Y', (3, 0), 'U')}
>>> print(board.move('Y', (3, 0), 'U'))
R R B .
. . Y R
B B . R
Y R Y Y
>>> board.possible_moves()
{('Y', (1, 0), 'U')}
>>> print(board.move('Y', (1, 0), 'U'))
R R B .
Y . Y R
B B . R
Y R Y Y
>>> board.possible_moves()
set()