Suppose that we have subdivided the rotating drum of a washing machine into sixteen equal parts, as shown in the left figure below. The dark segments represent conductive materials, whereas the lighter segments represent non-conductive materials. The position of the drum is represented by four binary digits $$a$$, $$b$$, $$c$$ and $$d$$ as shown in the right figure below. Depending on the position of the drum, the connection points represented by $$a$$, $$b$$, $$c$$ en $$d$$ either are grounded or insulated from the earth — in the example figure below the grounded connection points are $$a$$, $$c$$ and $$d$$. Grounded connection points send out a signal that is represented by 1, and isolated connection points send out a signal represented by 0.

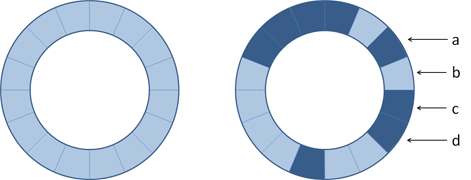
In order to ensure that each of the sixteen positions of the rotating drum can be represented in a unique way by a word $$abcd$$ of four binary digits, the conductive and non-conductive materials need to be allocated to the sixteen segments in such a way that each of the sixteen possible words of four binary digits $$abcd$$ occurs. The question that arises is whether this is possible. And if so, then how can the materials be ranked?

The right figure above immediately gives a solution to this problem. The position shown corresponds to the binary word 1011. If we rotate the drum counterclockwise we successively obtain the following sequence of binary words:

0110, 1100, 1001, 0010, 0100, 1000, 0000, 0001, 0011, 0111, 1111, 1110, 1101, 1010, 0101, 1011.

All of these words of four binary words are different, and together they form the sixteen possible positions of the rotating drum.

The problem of the rotating drum and its solution based on de Bruijn sequences, finds applications in computational biology, the generation of pseudo-random numbers, cryptography, telecommunications, and yes, even in the design of washing machines.

Algorithm

A de Bruijn sequence of order $$n$$ is a shortest possible (circular) binary string such that every sequence of $$n$$ bits appears as a substring at least once. For example, the string 0000111101100101 is a de Bruijn sequence of order 4, and all $$2^4$$ possible 4-bit sequences (0000, 0001, …, 1111) occur exactly once. A possible algorithm to generate a de Bruijn sequence of order $$n$$ works as follows:

start with a string of $$n$$ consecutive zeroes
append 1 to the end of the string if the $$n$$-digit suffix that would be formed this way has not already appeared in the sequence; otherwise a 0 is appended to the end of the string
repeat step 2 until the length of the sequence equals $$2^n$$

Input

An integer $$n \in \mathbb{N}_0$$.

Output

The de Bruijn sequence of order $$n$$ that results from the algorithm given above.

Example

Input:

Output:

0000111101100101