Given a number of cities that have to be visited by a salesman to sell a certain product. The salesman wants to minimise the travel time between the cities and return to the city where he started. This problem is known as the traveling salesman problem (TSP).
Find a route that visits each city exactly once and minimises the distance traveled.
We use a greedy approximation algorithm known as 2-opt in the context of TSP. The basic principle of this algorithm is to start with a route, and to improve it step by step by executing a local change.
For example: in this given route, replace C - A and D - B by A - B and C - D.
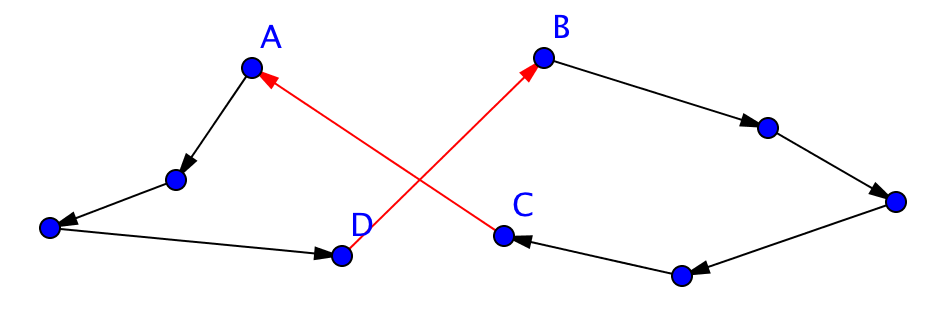
This changes the route:
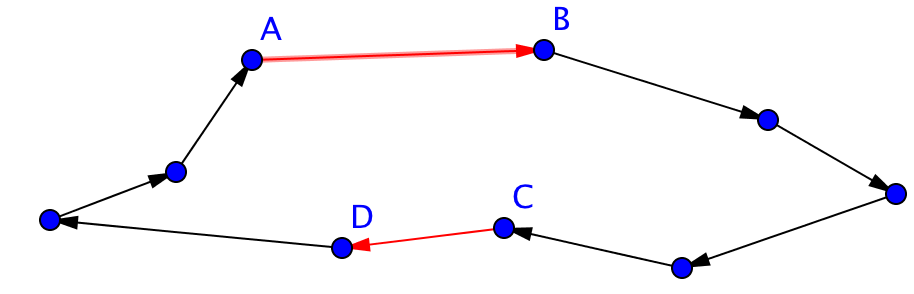
The cities between A and D have to be visited in reverse order, but since the distance is symmetric, the total distance is not changed.
The algorithm works like this:
- Start with a random travel
- repeat until no improvements are found:
- Evaluate all 2-opt changes until 1 is found that lowers the distance travelled
- If an improvement is found, execute it.
Assignment
Write a Python function TSP2opt(points: list): that takes a list of (x,y) coordinates and executes the TSP2opt algorithm on the given points.
The function returns the order in which the points have to be visited.
Examples
>>> TSP2opt([(0,0),(1,0),(0,1),(1,1)])`
[0,1,3,2]
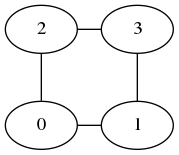
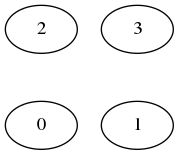 ->
-> 
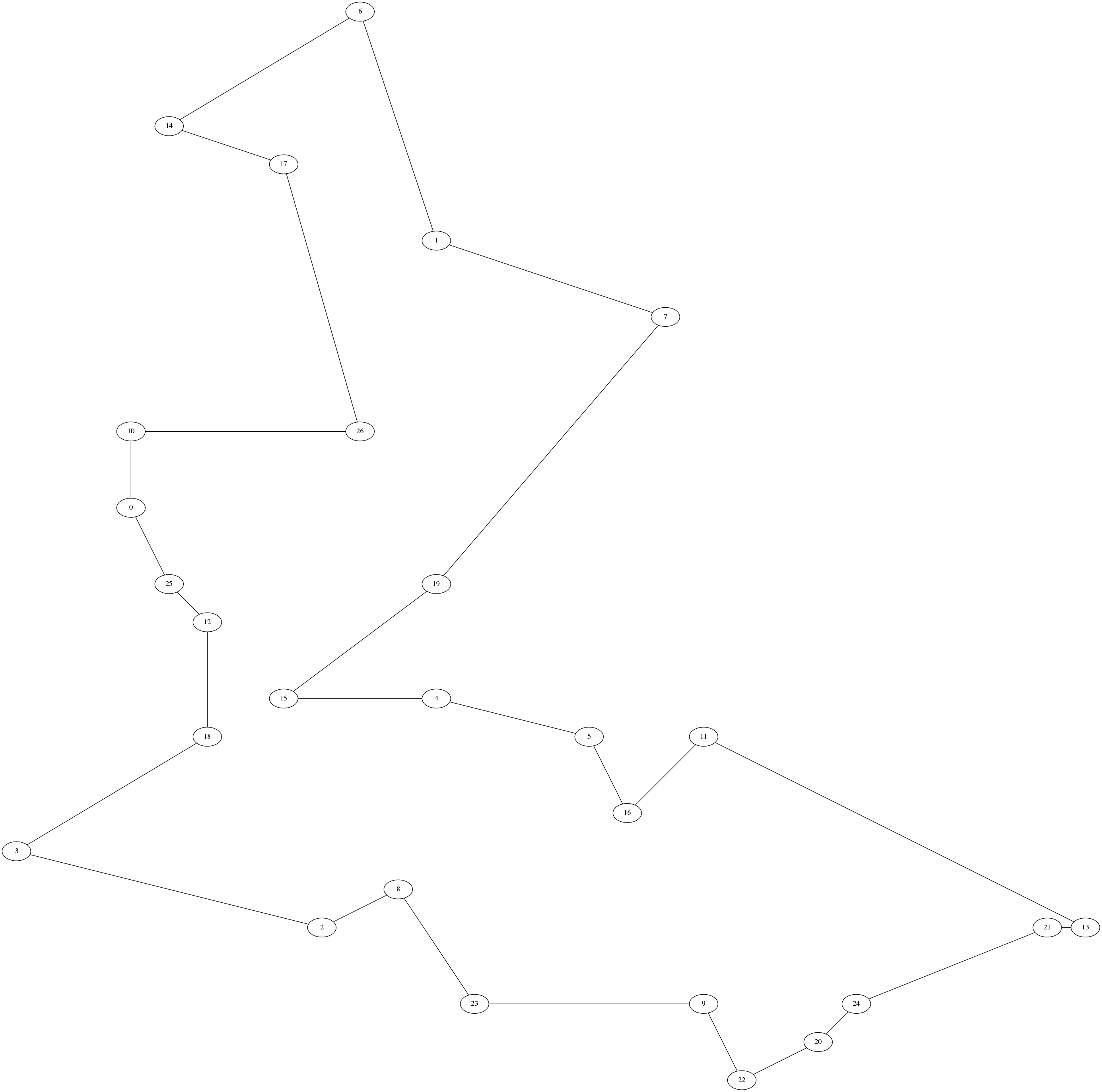
>>> TSP2opt([(3, 15), (11, 22), (8, 4), (0, 6), (11, 10), (15, 9), (9, 28), (17, 20), (10, 5), (18, 2), (3, 17), (18, 9), (5, 12), (28, 4), (4, 25), (7, 10), (16, 7), (7, 24), (5, 9), (11, 13), (21, 1), (27, 4), (19, 0), (12, 2), (22, 2), (4, 13), (9, 17)])
[0, 25, 12, 18, 3, 2, 8, 23, 9, 22, 20, 24, 21, 13, 11, 16, 5, 4, 15, 19, 7, 1, 6, 14, 17, 26, 10]
 ->
-> 
To visualise your solution, you can use this1.
Extra: There are a lot of possibilities to improve this algorithm. For example, you can design more complex changes to escape a local minimum. Feel free to experiment with your own ideas.