Invloedrijke observaties

In onderstaande code wordt data gesimuleerd om de impact van outliers te illustreren.

set.seed(112358)
nobs<-20
sdy<-1
x<-seq(0,1,length=nobs)
y<-10+5*x+rnorm(nobs,sd=sdy)
x1<-c(x,0.5)
y1 <- c(y,10+5*1.5+rnorm(1,sd=sdy))
x2 <- c(x,1.5)
y2 <- c(y,y1[21])
x3 <- c(x,1.5)
y3 <- c(y,11)
plot(x,y,xlim=range(c(x1,x2,x3)),ylim=range(c(y1,y2,y3)))
points(c(x1[21],x2[21],x3[21]),c(y1[21],y2[21],y3[21]),pch=as.character(1:3),col=2:4)
abline(lm(y~x),lwd=2)
abline(lm(y1~x1),col=2,lty=2,lwd=2)
abline(lm(y2~x2),col=3,lty=3,lwd=2)
abline(lm(y3~x3),col=4,lty=4,lwd=2)
legend("topleft",col=1:4,lty=1:4,legend=paste("lm",c("",as.character(1:3))),text.col=1:4)

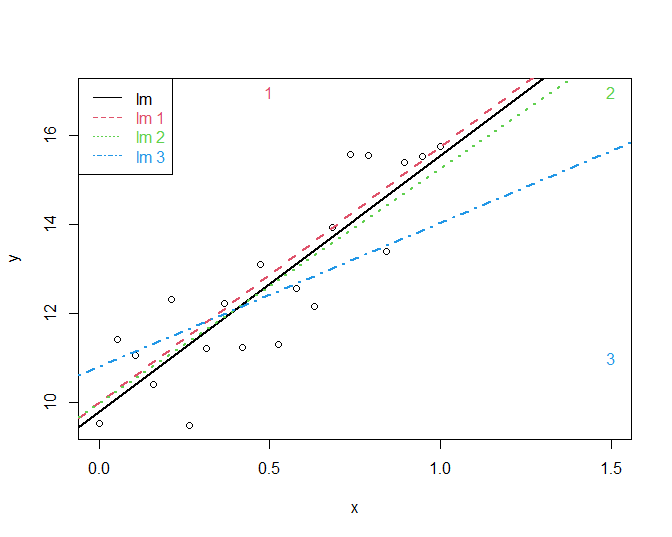
Figuur 66: Impact van outliers op de regressie. Regressie zonder outliers (zwart), regressie met outlier 1 (groen), regressie met outlier 2 (rood), regressie met outlier 3 (blauw).

Een dataset bevat vaak extreme observaties voor zowel de uitkomst $Y$ als de predictoren $X$ . Deze kunnen de geschatte regressieparameters en regressielijn sterk beïnvloeden. Dat is niet verwonderlijk vermits de regressielijn de gemiddelde uitkomst voorstelt in functie van $X$ en gemiddelden zeer gevoelig zijn aan outliers. Figuur 66 toont een puntenwolk met 3 afwijkende observaties samen met 4 lineaire regressielijnen één zonder en één met elk van deze observaties. Merk op dat de regressielijn in bijzondere mate afwijkt wanneer observatie 3 wordt opgenomen in de dataset. Dit kan als volgt worden verklaard. De aanwezigheid van observatie 1 impliceert dat de regressielijn (en bijgevolg het intercept) naar boven wordt getrokken, maar heeft verder geen invloed op het patroon van de regressielijn. Observatie 2 is extreem, maar heeft geen impact op de regressielijn omdat ze het patroon van de rechte volgt. Hoewel observatie 3 niet met een zeer extreme uitkomst $y$ overeenstemt, zal deze observatie toch het meest invloedrijk zijn omdat de predictorwaarde $x$ en, in het bijzonder, de $(x, y)$ -combinatie zeer afwijkend is.

Het spreekt voor zich dat het niet wenselijk is dat een enkele observatie het resultaat van een lineaire regressie-analyse grotendeels bepaalt. We wensen daarom over diagnostieken te beschikken die ons toelaten om extreme observaties op te sporen. Residu’s geven weer hoe ver de uitkomst afwijkt van de regressielijn en kunnen bijgevolg gebruikt worden om extreme uitkomsten te identificeren. In het bijzonder hebben we eerder vermeld dat residu’s bij benadering Normaal verdeeld zijn wanneer het model correct is en de uitkomst Normaal verdeeld (bij vaste predictorwaarden) met homogene variantie. Of een residu extreem is, kan in dat opzicht geverifieerd worden door haar te vergelijken met de Normale verdeling. Stel bijvoorbeeld dat men over 100 observaties beschikt, dan verwacht men dat ongeveer 5% van de residu’s in absolute waarde extremer zijn dan 1.96 $\hat{σ}$ . Indien men veel meer extreme residu’s observeert, dan is er een indicatie op outliers.

In de literatuur heeft men een aantal modificaties van residu’s ingevoerd met als doel deze nuttiger te maken voor de detectie van outliers. Studentized residu’s zijn een transformatie van de eerder gedefinieerde residu’s die $t$ -verdeeld zijn met $n - 1$ vrijheidsgraden onder de onderstellingen van het model. Outliers kunnen aldus nauwkeuriger worden opgespoord door na te gaan of veel meer dan 5% van de studentized residu’s in absolute waarde het 97.5% percentiel van de $t_{n - 1}$ -verdeling overschrijden.

Extreme predictorwaarden kunnen in principe opgespoord worden via een scatterplot matrix voor de uitkomst en verschillende predictoren. Wanneer er meerdere predictoren zijn, hebben deze echter ernstige tekortkomingen omdat het een combinatie van meerdere predictoren kan zijn die ongewoon is en dit niet kan opgespoord worden via dergelijke grafieken. Om die reden is het veel zinvoller om de zogenaamde leverage (invloed, hefboom) van elke observatie te onderzoeken. Dit is een diagnostische maat voor de mogelijkse invloed van predictor-observaties (in tegenstelling tot de residu’s die een diagnostische maat vormen voor de invloed van de uitkomsten). In het bijzonder is de leverage van de $i$ -de observatie een maat voor de afstand van predictorwaarde voor de $i$ -de observatie tot de gemiddelde predictorwaarde in de steekproef. Hieruit volgt bijgevolg dat indien de leverage voor de $i$ -de observatie groot is, ze predictorwaarden heeft die sterk afwijken van het gemiddelde. In dat geval heeft die observatie mogelijks ook grote invloed op de regressieparameters en predicties. Leverage waarden variëren normaal tussen $1 / n$ en 1 en zijn gemiddeld $p / n$ met $p$ het aantal ongekende parameters (intercept + $p - 1$ hellingen). Een extreme leverage wordt typisch aanschouwd als een waarde groter dan $2 p / n$ .

Cook’s distance

Een meer rechtstreekse maat om de invloed van elke observatie op de regressie-analyse uit te drukken is de Cook’s distance. De Cook’s distance voor de $i$ -de observatie is een diagnostische maat voor de invloed van die observatie op alle predicties of, equivalent, voor haar invloed op alle geschatte parameters. Men bekomt deze door elke predictie ${\hat{Y}}_{j}$ die men op basis van het regressiemodel heeft bekomen voor de $j$ -de uitkomst, $j = 1, . . ., n$ , te vergelijken met de overeenkomstige predictie ${\hat{Y}}_{j (i)}$ die men zou bekomen indien de $i$ -de observatie niet gebruikt werd om het regressiemodel te fitten

D_{i} = \frac{\sum_{j = 1}^{n} ({\hat{Y}}_{j} - {\hat{Y}}_{j (i)})^{2}}{p MSE}

Indien de Cook’s distance $D_{i}$ groot is, dan heeft de $i$ -de observatie een grote invloed op de predicties en geschatte parameters. In het bijzonder stelt men dat een extreme Cook’s distance het 50% percentiel van de $F_{p, n - p}$ -verdeling overschrijdt.

Deze plots komen standaard bij diagnose van het lineair model. We evalueren dit voor het additieve model en het model met de lcavol:lweight interactie voor de prostaatkanker studie.

par(mfrow=c(2,2))
plot(lmVWS,which=5)
plot(lmVWS_IntVW,which=5)
plot(cooks.distance(lmVWS),type="h",ylim=c(0,1),main="Additive model")
abline(h=qf(0.5,length(lmVWS$coef),nrow(prostate)-length(lmVWS$coef)),lty=2)
plot(cooks.distance(lmVWS_IntVW),type="h",ylim=c(0,1), main="Model with lcavol:lweight interaction")
abline(h=qf(0.5,length(lmVWS_IntVW$coef),nrow(prostate)-length(lmVWS_IntVW$coef)),lty=2)

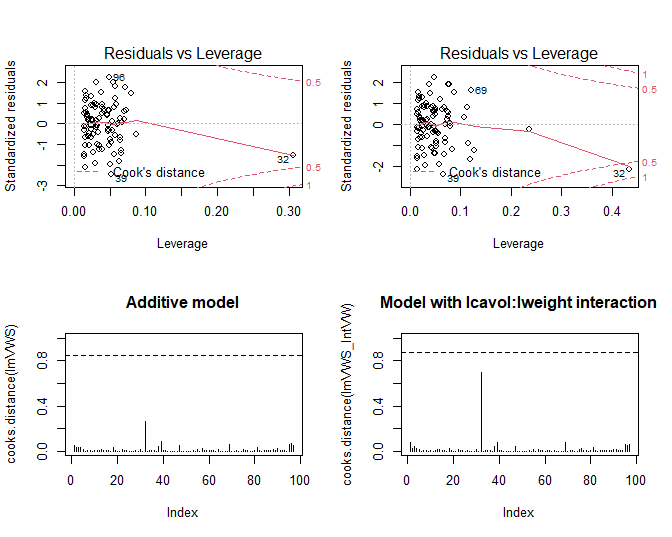
Figuur 67: Evaluatie van de invloed van individuele observaties op het additieve model (links) en het model met de lcavol:lweight interactie (rechts).

Het is duidelijk dat observatie 32 een grote leverage heeft. Het heeft in het model met interactie ook de grootste invloed van alle datapunten op de fit van het model.

Eenmaal men vastgesteld heeft dat een observatie invloedrijk is, kan men zogenaamde DFBETAS gebruiken om te bepalen op welke parameter(s) ze een grote invloed uitoefent. De DFBETAS van de $i$ -de observatie vormen een diagnostische maat voor de invloed van die observatie op elke regressieparameter afzonderlijk, in tegenstelling tot de Cook’s distance die de invloed op alle parameters tegelijk evalueert. In het bijzonder bekomt men de DFBETAS voor de $i$ -de observatie en de $j$ -de parameter door de $j$ -de parameter ${\hat{β}}_{j}$ te vergelijken met de parameter ${\hat{β}}_{j (i)}$ die men zou bekomen indien het regressiemodel gefit werd zonder de $i$ -de observatie in de analyse te betrekken:

{DFBETAS}_{j (i)} = \frac{{\hat{β}}_{j} - {\hat{β}}_{j (i)}}{SD ({\hat{β}}_{j})}

Uit bovenstaande uitdrukking volgt dat het teken van de DFBETAS voor de $i$ -de observatie aangeeft of het weglaten van die observatie uit de analyse een stijging (DFBETAS $< 0$ ) of daling (DFBETAS $> 0$ ) in de overeenkomstige parameter veroorzaakt. In het bijzonder stelt men dat een DFBETAS extreem is wanneer ze 1 overschrijdt in kleine tot middelgrote datasets en $2 / \sqrt{n}$ overschrijdt in grote datasets.

par(mfrow=c(2,2))
dfbetasPlots(lmVWS)

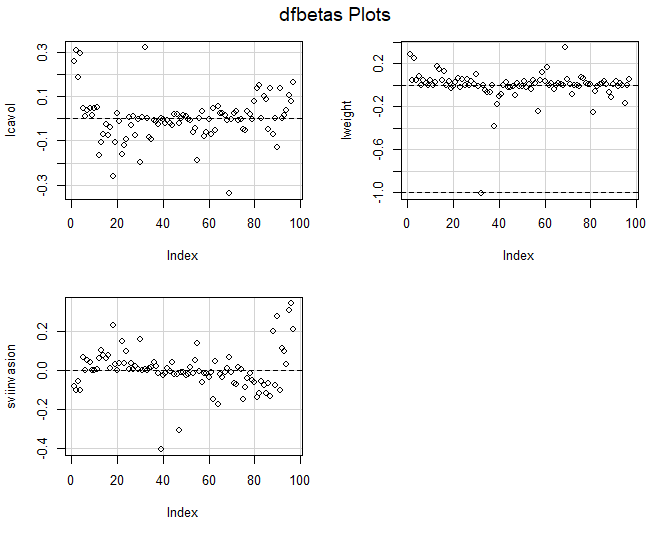
Figuur 68: DFBETAS voor additieve model in prostaatkanker.

par(mfrow=c(2,2))
dfbetasPlots(lmVWS_IntVW)

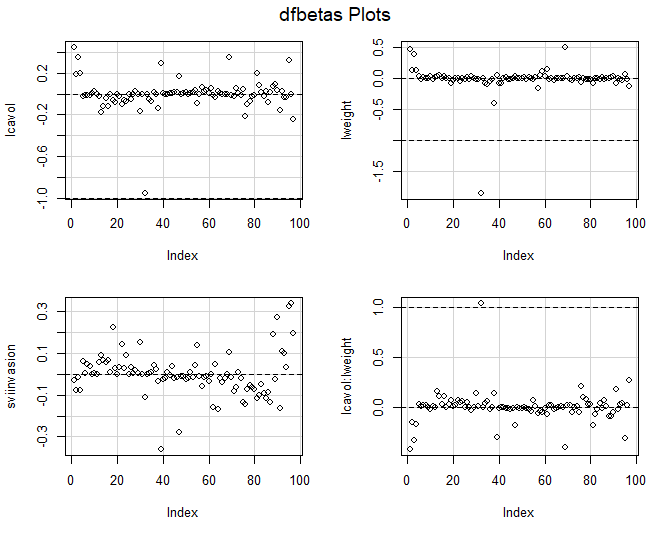
Figuur 69: DFBETAS voor model met lcavol:lweight interactie.

De Cooks distances en de DFBETAS plots geven aan dat observatie 32 het grootste effect heeft op de regressieparameters. Daarnaast heeft deze observatie ook een extreme “influence”.

We gaan observatie 32 nu wat beter bestuderen.

exp(prostate[32,"lweight"])

## # A tibble: 1 x 1
##   lweight
##     <dbl>
## 1    449.

boxplot(exp(prostate$lweight),ylab="Prostaatgewicht (g)")

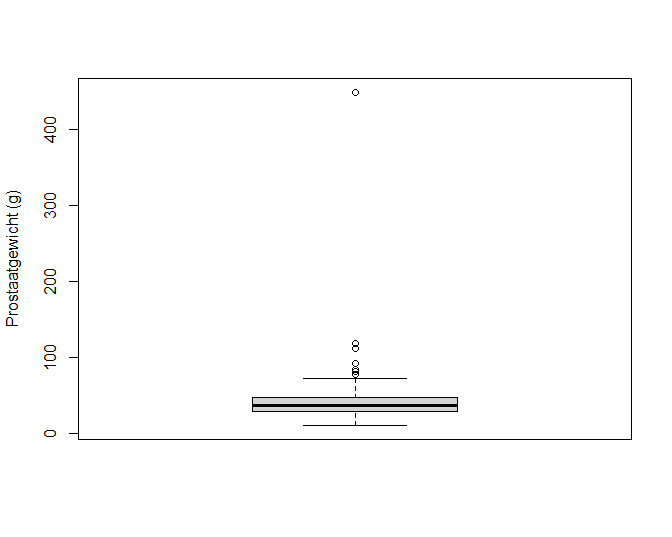
Figuur 70: Boxplot met outlier voor prostaatgewicht.

Wanneer we het gewicht terugtransformeren naar de originele schaal zien we dat het prostaatgewicht voor deze patiënt449.25g bedraagt. De prostaat van een man heeft gewoonlijk een gewicht van 20-30 gram en het kan vergroten tot 50-100 gram. Een prostaatgewicht van meer dan 400 gram komt dus niet voor. De auteurs die de dataset uit de originele publicatie hebben opgenomen in een handboek, hebben gerapporteerd dat ze een tikfout hebben gemaakt en ze hebben het extreme prostaat gewicht later gecorrigeerd naar 49.25 gram, het gewicht dat in de originele publicatie werd gerapporteerd.

Ga zelf na welke invloed het corrigeren van het prostaatgewicht heeft op het geschatte regressiemodel.