Powerful numbers are positive integers that equal the sum of the $$n$$-th powers of their digits for some $$n \in \mathbb{N}$$. The smallest $$n$$ for which this property holds is called the order of the powerful number.
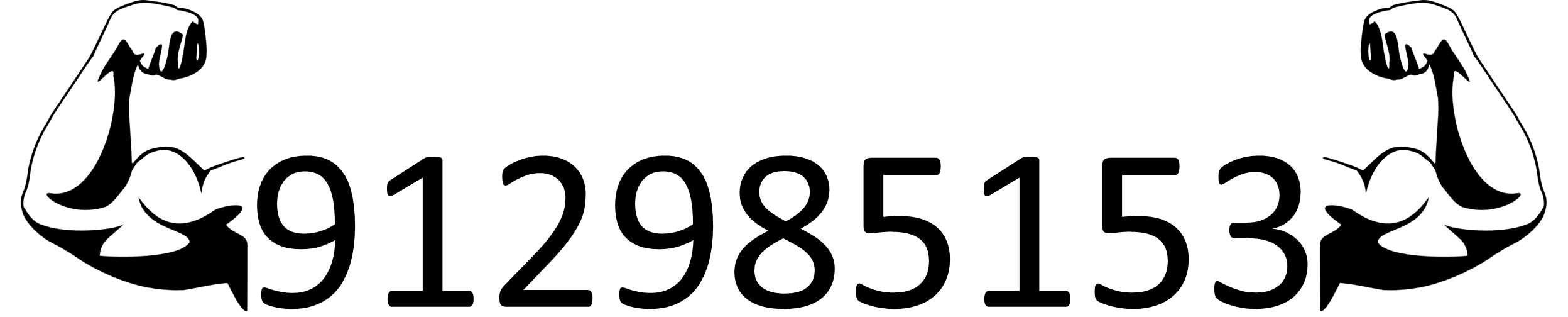
Consider, for example, the number 912985153. This is a powerful number of order 9 because \[9^9 + 1^9 + 2^9 + 9^9 + 8^9 + 5^9 + 1^9 + 5^9 + 3^9 = 912985153\]
Input
An integer $$m \in \mathbb{N}$$.
Output
A line that indicates whether or not $$m \in \mathbb{N}$$ is a powerful number. In case $$m \in \mathbb{N}$$ is a powerful number, the output must also indicate the order $$n \in \mathbb{N}$$ of the powerful number. The format of the output can be derived from the examples below.
Example
Input:
912985153Output:
912985153 is a powerful number of order 9Example
Input:
123456789
Output:
123456789 is not a powerful number