Temple University¹ anthropologist Wayne Zachary was studying a local karate club in the early 1970s when a disagreement arose between the club’s instructor and its president, dividing the club’s 34 members into two factions. By studying the communication flow among the members, Zachary was able to predict correctly, with one exception, which side each member would take in the dispute between the club's instructor and its president.

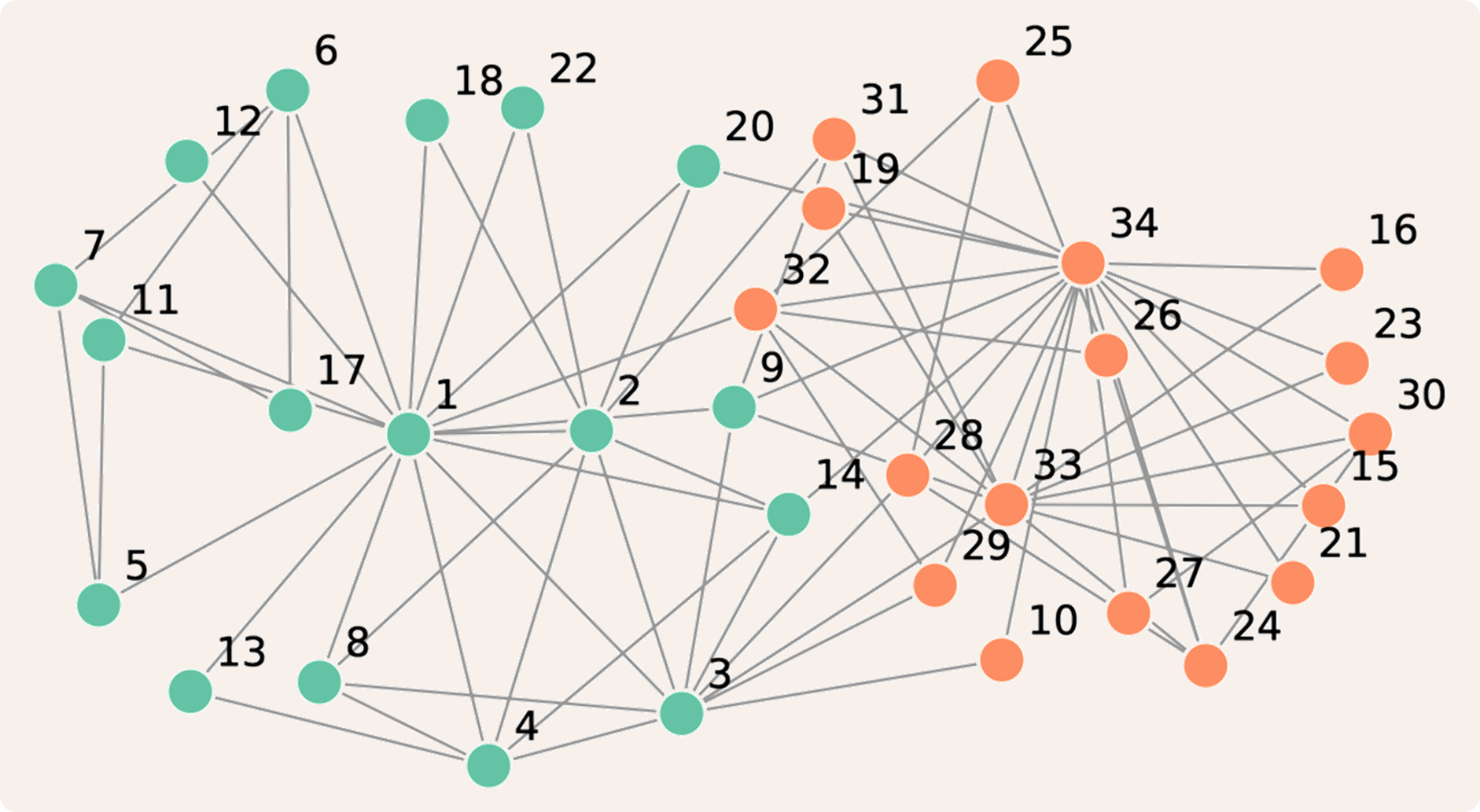
This episode has become a popular example in discussions of community structure in networks, so much so that scientists now award a trophy to the first person to use it at a conference. The original example is known as Zachary’s Karate Club; the trophy winners are the Zachary’s Karate Club Club².

Assignment

In a network $$\mathcal{N}$$ with $$n$$ nodes, the nodes are numbered from 1 to $$n$$. The capacity $$c_{i,j}$$ is a measure of the strength of the communication flow between node $$i$$ and node $$j$$ in network $$\mathcal{N}$$: the higher the capacity, the stronger the communication flow between the two nodes. We only consider networks whose capacities satisfy the following conditions:

• $$c_{i,j} \in \mathbb{N}$$, with $$0 \leq c_{i,j} < 10$$ for all $$1 \leq i, j \leq n$$

• $$c_{i,j} = c_{j,i}$$ for all $$1 \leq i, j \leq n$$

• $$c_{i,i} = 0$$ for all $$1 \leq i \leq n$$

A capacity file for a network $$\mathcal{N}$$ is a text file that describes all capacities of the network. The file contains $$n$$ lines that each consist of $$n$$ digits (0–9). If we number the lines from top to bottom starting at 1, and also number the positions of the digits on each line from left to right starting at 1, then the $$j$$-th digit on line $$i$$ represents the capacity $$c_{i,j}$$ of network $$\mathcal{N}$$. For example, this is the capacity file for the 34 members of Zachary's Karate Club (karate.txt³):

0453333220232300020202000000000200
4063000400000500010202000000002000
5603000451000300000000000002200030
3330000300003300000000000000000000
3000002000300000000000000000000000
3000005000300000300000000000000000
3000250000000000300000000000000000
2443000000000000000000000000000000
2050000000000000000000000000003043
0010000000000000000000000000000002
2000330000000000000000000000000000
3000000000000000000000000000000000
2003000000000000000000000000000000
3533000000000000000000000000000003
0000000000000000000000000000000032
0000000000000000000000000000000034
0000033000000000000000000000000000
2100000000000000000000000000000000
0000000000000000000000000000000012
2200000000000000000000000000000001
0000000000000000000000000000000031
2200000000000000000000000000000000
0000000000000000000000000000000020
0000000000000000000000000504020054
0000000000000000000000000203000200
0000000000000000000000052000000700
0000000000000000000000000000040002
0020000000000000000000043000000004
0020000000000000000000000000000202
0000000000000000000000020040000042
0200000030000000000000000000000033
2000000000000000000000002700200044
0030000040000033001030250000043405
0000000032000324002110340024223450

A group of nodes of a network $$\mathcal{N}$$ with $$n$$ nodes is a collection (list, tuple or set) containing the node numbers (int). As such, the collection may only consist of integers between 1 and $$n$$. Moreover, each node number may occur at most once in the collection. The order of the node numbers in the collection plays no role.

Your task:

• Write a function read_network that takes the location (str) of a capacity file for a network $$\mathcal{N}$$. The function must return a dictionary (dict) that maps each node $$i$$ (int) in network $$\mathcal{N}$$ onto a dictionary (dict) that maps each node $$j$$ (int) for which $$c_{i,j} > 0$$ in network $$\mathcal{N}$$ onto the capacity $$c_{i,j}$$ (int) of network $$\mathcal{N}$$. The result returned by this function is called the capacity dictionary of network $$\mathcal{N}$$.

• Write a function complementary_group that takes two arguments: i) a group $$g$$ (list, tuple or set) with nodes (int) of a network $$\mathcal{N}$$ and ii) the capacity dictionary (dict) of network $$\mathcal{N}$$. If the first argument does not represent a valid group, the function must raise an AssertionError with message invalid group. Otherwise, the function must return the complementary group $$\bar{g}$$: a set (set) with all nodes (int) of network $$\mathcal{N}$$ that do not belong to group $$g$$.

• Write a function flow that takes two arguments: i) a group $$g$$ (list, tuple or set) with nodes (int) of a network $$\mathcal{N}$$ and ii) the capacity dictionary (dict) of network $$\mathcal{N}$$. If the first argument does not represent a valid group, the function must raise an AssertionError with message invalid group. Otherwise, the function must return the strength of the communication flow (int) between group $$g$$ and its complementary group $$\bar{g}$$: the sum of all capacities $$c_{i,j}$$ for all $$i \in g$$ and all $$j \in \bar{g}$$.

Example

In this interactive session we assume the text file karate.txt⁴ to be located in the current directory.

>>> network = read_network('karate.txt5')
>>> network[11]
{1: 2, 5: 3, 6: 3}
>>> network[24]
{26: 5, 28: 4, 30: 2, 33: 5, 34: 4}

>>> group = [1, 2, 3, 4, 5, 6, 7, 8, 11, 12, 13, 14, 17, 18, 20, 22]
>>> complementary_group(group, network) # doctest: +SKIP
{9, 10, 15, 16, 19, 21, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34}
>>> complementary_group((1, 2, 3, 2), network)
Traceback (most recent call last):
AssertionError: invalid group

>>> flow(group, network)
23
>>> flow(set(group) | {9}, network)
26
>>> flow((1, 2, 3, 2), network)
Traceback (most recent call last):
AssertionError: invalid group

Sources

• Girvan M, Newman ME (2002). Community structure in social and biological networks. Proceedings of the national academy of sciences 99(12), 7821–7826. ⁶

• Zachary WW (1977). An information flow model for conflict and fission in small groups. Journal of anthropological research 33(4), 452–473. ⁷