Trilateration is the process of determining absolute or relative locations of points by measurement of distances, using the geometry of circles or spheres. In addition to its interest as a geometric problem, trilateration does have practical applications in surveying and navigation, including global positioning systems (GPS) and determining epicenters of earthquakes. In contrast to triangulation, trilateration does not involve the measurement of angles. In two-dimensional geometry, it is known that if a point lies on two circles, then the circle centers and the two radii provide sufficient information to narrow the possible locations down to two. Additional information may narrow the possibilities down to one unique location.
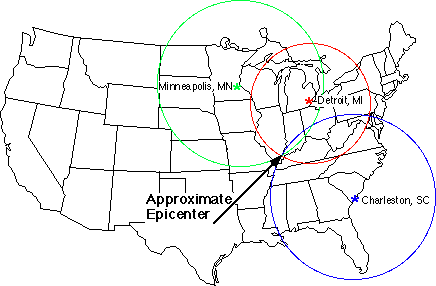
For example, this is how trilateration can be used to determine the epicenter of an earthquake. During an earthquake, seismic waves1 propagate spherically out from the hypocenter. Seismic shadowing2 occurs on the opposite side of the Earth from the earthquake epicenter because the liquid outer core refracts the longitudinal or compressional (P-waves3) while it absorbs the transverse or shear waves (S-waves4). Outside of the seismic shadow zone both types of wave can be detected but, due to their different velocities and paths through the Earth, they arrive at different times. By measuring the time difference on any seismograph as well as the distance on a travel-time graph at which the P-wave and S-wave have the same separation, geologists can calculate the distance to the earthquake's epicenter. This distance is called the epicentral distance.
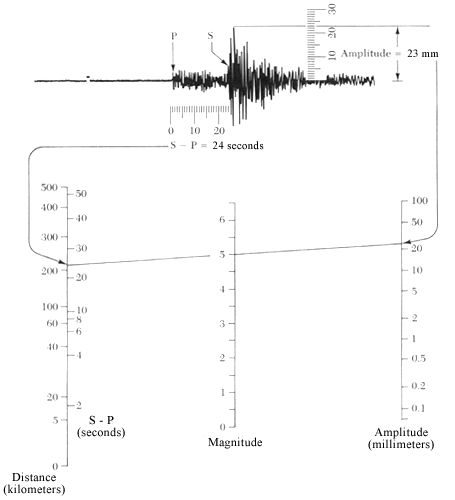
In the picture below we see that a difference of 24 seconds between the first P-wave and the first S-wave corresponds to an epicenter in a 215 km radius. Drawing a circle centered in the measuring station with a radius of 215 km, we can locate the epicenter somewhere around the circle. Once epicentral distances have been calculated from at least three seismographic measuring stations, it is thus a simple matter to find out where the epicenter was located by finding the point where the circles intersect. In practice, however, there will always be a mistake in the measurements and the circles will never really intersect. As a result, we will find a narrow zone of possible locations of the epicenter.
Assignment
An important subtask of trilateration is determining the relative position of two circles. In the following table, you can find an overview of all possible relative positions of two circles, where $$d$$ indicates the distance between the centers of both circles and $$r_1$$ (respectively $$r_2$$) indicates the radius of the first (respectively the second) circle.
| position | condition |
|---|---|
| concentric | $$d = 0$$ |
| touching inside | $$d = |r_1 - r_2|$$ |
| touching outside | $$d = r_1 + r_2$$ |
| enclosing | $$d < |r_1 - r_2|$$ |
| intersecting | $$|r_1 - r_2| < d < r_1 + r_2$$ |
| separate | $$d > r_1 + r_2$$ |
The distance $$d$$ between two points $$(x_1, y_1)$$ and $$(x_2, y_2)$$ is calculated using the formula:
$$d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$$
Warning
If you work with floating point numbers on a computer, you will often be confronted with rounding errors. As a result, real valued numbers that are equal in a mathematical sense might turn out to be not equal in computing. As a result, we always use a small margin of error while comparing floating point numbers: for example, we say that two floating point numbers are equal if they do not differ more than, let's say, $$10^{-6}$$.
Input
Six real valued numbers: one number per line. The first three numbers are the $$x$$-coordinate, the $$y$$-coordinate and the radius of a first circle. The last three numbers are the $$x$$-coordinate, the $$y$$-coordinate and the radius of a second circle.
Output
The output contains one of the following terms:
-
concentric
-
touching inside
-
touching outside
-
enclosing
-
intersecting
-
separate
The outputted term must describe the relative position of the two given circles.
Example
Input:
3.5
2.7
7.86
6.5
6.7
2.86Output:
touching insideFrom the graphical representation of the two given circles, we can clearly see that they indeed touch each other on the inside. The first circle is depicted in orange, the second circle in purple.