The audience was stunned when contestant Michael Larson won $110.237 on Press Your Luck in 1984. Easily the largest one-day total ever won on a game show to that date. As lights flashed randomly on the Big Board — the name given to the eighteen-square gameboard used in the show — somehow Larson was consistently able to stop on squares that led to cash and additional play, and avoid the "whammy" that would bankrupt him.

Paul Michael Larson

It turned out that the light indicator wasn't random. In studying the game at home, Larson had discovered that it followed five recognizable patterns. After memorizing these he could always be sure of landing on winning squares.

CBS producers divined the scheme, but they could find no cause to disqualify Larson, as he had broken no rules. They paid him his money, fixed the board, and established a maximum sum that future contestants could win. Larson may have congratulated himself, but he didn't get to enjoy his winnings — he lost the money in bad real estate investments and died of throat cancer at age 49.

Assignment

Below is an example configuration of the Big Board, the gameboard used in the television show Press Your Luck. The board consisted of $$p$$ squares (in the example $$p = 18$$) arranged in a rectangle, each of which displayed one of $$s$$ screens (in the example $$s = 3$$). If a player took turn, a fast cycle was initiated where at each step all squares displayed the next screen and a random square lit up. The player could stop the cycle by hitting his buzzer, which either won him the price that was shown on the screen marked by the randomizer light or made him loose al his money if he hit a screen marked with the whammy.

Configuration of the Big Board, the game board that was used in the television show Press Your Luck. The board is composed of 18 square, with each square showing one of three screens in turn. The "+S" denotes screens that award contestants an additional spin, a feature critical to allowing Larson to go on his run.

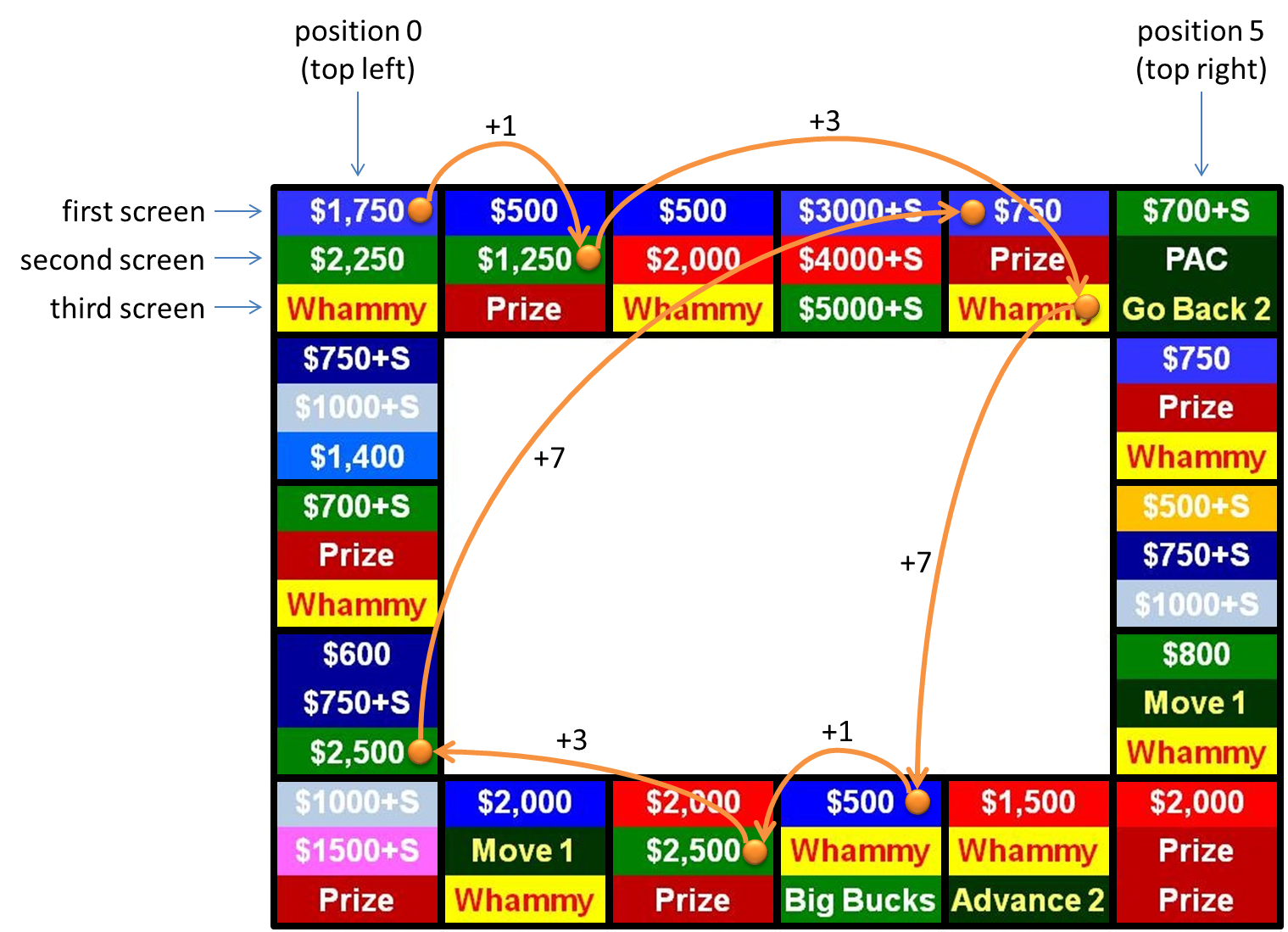
However, Larson had discovered a certain regularity in the apparently random behaviour of the gameboard. Each cycle turned out to be completely determined by a pattern that was composed of a sequence of positive integers and a square that was lit at the start of the cycle. At each step in the cycle, the gameboard is modified in two ways, that work completely independent of each other:

The next square that is lit is determined by selecting the next integer $$m$$ from the pattern (starting at the first number, and returning to the first number after the last number), and moving clockwise to the screen that is $$m$$ positions upstream on the gameboard. The rectangular configuration of the gameboard causes the last square to be followed by the first square.
At the start of a cycle, each square shows its first screen. Each step of the cycle switches all squares to their next screen from the sequence of $$s$$ screens, where the last screen is followed again by the first screen from the sequence.

The above figure illustrates this procedure with a cycle that uses the pattern [1, 3, 7] and starts at the square in the top left-hand of the gameboard. At the start of the cycle, the square in the top left-hand of the gameboard displays the screen containing $1750, the square to the right displays the screen containing $500, and so on. In the first step the randomizer light moves ahead 1 square clockwise through the rectangular board, and each square displays its second screen. If we would hit the buzzer at this point in time, the screen containing $1250 would be lit. In the second stap the randomizer light moves ahead 3 squares clockwise through the rectangular board, and the third screen containing whammy is lit. In the next step the randomizer light moves ahead 7 squares clockwise through the rectangular board, and the first screen displaying $500 is lit (during the previous step, each square displayed the last of its three screens). In the next step the randomizer light again moves ahead 1 square clockwise through the rectangular board (after the last integer from the pattern has been used, we continue with the first integer), and the second screen containing $2500 is lit. The figure continues to show the next two steps from the cycle. Your task:

Write a function board that takes a sequence (a list or a tuple) of strings. This sequence of strings represents the prices (or Whammies) that are used to configure a Big Board with $$s \in \mathbb{N}_0$$ screens per square. The value $$s$$ can be passed to the second optional parameter screens (default value: 1). The function must return a list of squares, where each square is represented as a list that is filled with the next $$s$$ strings from the given sequence of strings. Each square thus represents a sequence of screens containing prices that are displayed round robin at the position of that square.
Use the function board to write a function price. The function must return the price (string) that is lit up on the gameboard after it has cycled a given number of steps using a given pattern and a given starting position. The gameboard, the number of steps, the pattern and the starting position are determined by the values passed to the mandatory and optional parameters of the function:

pattern (mandatory): sequence (list or tuple) of integers $$\in \mathbb{N}_0$$ that describes the pattern
steps (mandatory): integer $$\in \mathbb{N}_0$$ that indicates the number of steps
prices (mandatory): sequence (list or tuple) of strings that describes the gamebord (see function board)
start (optional; default value: 0): integer $$\in \mathbb{N}_0$$ that indicates the position of the square where the cycle starts; squares are indexed clockwise, starting at the square in the top left-hand corner that is at position 0
screens (optional; default value: 1): integer $$\in \mathbb{N}_0$$ that indicates the number of screens per square (see function board)

Both functions must raise an AssertionError with the message invalid board, in case the number of prices in the given sequence of strings is not a multiple of $$s$$.

Example

>>> prices = ('$100', '$200', '$300', '$400', '$500', '$600', '$700', '$800', '$900', '$1000', 'whammy', '$1100', '$1200', '$1300', '$1400', '$1500')

>>> board(prices)
[['$100'], ['$200'], ['$300'], ['$400'], ['$500'], ['$600'], ['$700'], ['$800'], ['$900'], ['$1000'], ['whammy'], ['$1100'], ['$1200'], ['$1300'], ['$1400'], ['$1500']]
>>> board(prices, screens=2)
[['$100', '$200'], ['$300', '$400'], ['$500', '$600'], ['$700', '$800'], ['$900', '$1000'], ['whammy', '$1100'], ['$1200', '$1300'], ['$1400', '$1500']]
>>> board(prices, screens=4)
[['$100', '$200', '$300', '$400'], ['$500', '$600', '$700', '$800'], ['$900', '$1000', 'whammy', '$1100'], ['$1200', '$1300', '$1400', '$1500']]
>>> board(prices, screens=3)
Traceback (most recent call last):
AssertionError: invalid board

>>> price(pattern=[1, 3, 7], steps=1, prices=prices, screens=2)
'$400'
>>> price(pattern=[1, 3, 7], steps=2, prices=prices, screens=2, start=1)
'whammy'
>>> price(pattern=[5, 2, 9, 3], steps=20, prices=prices, screens=4, start=4)
'$1200'