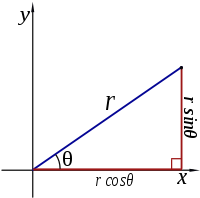
There are two common ways to represent each point of a surface by a pair of co-ordinates: Cartesian co-ordinates and polar co-ordinates. The first coordinate system is the best known. Here, each point is represented by a $$x$$ and a $$y$$ co-ordinate. In the second co-ordinate system, each point is represented by a radius $$r$$ (the distance from the origin), and an angle $$\theta$$ (the angle between the link to the origin and the positive $$X$$ axis). Of course there is a connection between these two co-ordinate systems. If a point has the co-ordinates $$(x,y)$$ and $$(r,\theta)$$, then the following relationships apply: \[\begin{cases} x = & r \cos(\theta) \\ \\ y= & r\sin(\theta) \end{cases}\] en \[\begin{cases} r = & \sqrt{x^2+y^2} \\ \\ \theta = & \arctan\left(\frac{y}{x}\right) \end{cases}\]

To solve this exercise you need functions from the math module. These functions are not available by default in a Python program, but you can make them readily available by placing the following line at the head of your code

from math import *

Later we will see a better way to only insert the functions that you need. What functions are available in the math module, can be checked by running the following commands in an interactive Python session:

>>> import math
>>> help(math)

Input

The Input consists of two real numbers, each on a separate line, representing respectively the $$x$$ and $$y$$ co-ordinate of a given point in the Cartesian co-ordinate system.

Output

The output consists of two real numbers, each on a separate line, respectively the radius $$r$$ and the angle $$\theta$$ of the given point, expressed in polar co-ordinates.

Example

Input:

1.0
0.0

Output:

1.0
0.0

Example2

Input:

0.0
3.0

Output:

3.0
1.5707963267948966