Continue toevallig veranderlijke

Een continue toevallig veranderlijke kan binnen bepaalde grenzen alle mogelijke waarden aannemen. De kans dat een continue toevallige veranderlijke exact één bepaalde waarde aan te nemen is daarom gelijk aan 0.

De distributie (verdeling) wordt daarom weergegeven a.d.h.v. de densiteitsfunctie of de dichtheidsfunctie \(f(x)\)

Veel biologische karakteristieken zijn approximatief normaal verdeeld (lengte, bloeddruk, IQ, concentratie metingen na logaritmische transformatie)

\[f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

Dat wordt kort genoteerd als

\[f(x) = N(\mu,\sigma^2)\]

Van het IQ is geweten dat het normale verdeling volgt met gemiddelde \(\mu=100\) en standaardafwijking \(\sigma=15\).

\[IQ \sim N(100,15^2)\]

In R kunnen we de dnorm functie gebruiken om de densiteit te berekenen voor een bepaalde waarde X=x.

iq <- tibble(
  IQ = seq(40,150,.1),
  Densiteit = dnorm(seq(40,150,.1),mean=100,sd=15)
  )
iq %>%
  ggplot(aes(x=IQ,y=Densiteit)) +
  geom_line()

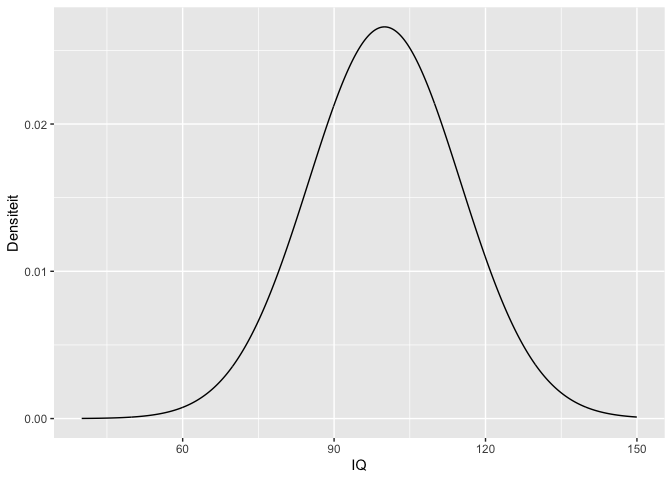
Binnen bepaalde grenzen kunnen continue toevallig veranderlijken alle mogelijke waarden aannemen dus is \(\Omega\) oneindig groot.

Cumulatieve distributie

Opnieuw is de cumulatieve distributie

\[F(X)=Pr(X\leq x).\]

Omdat X continu is berekenen we deze probabiliteit a.d.h.v. een integraal

\[F(x)=\int \limits_{-\infty}^x f(x) dx\]

Merk op dat \(f(x)=0\) als x niet tot de steekproefruimte behoord.

We kunnen \(F(x)\) berekenen voor een normaal verdeelde toevallig veranderlijke met de functie pnorm die opnieuw argumenten mean en sd heeft.

iq %>%
  mutate(Probability=pnorm(IQ,mean=100,sd=15)) %>%
  ggplot(aes(x=IQ,y=Probability)) +
  geom_line()

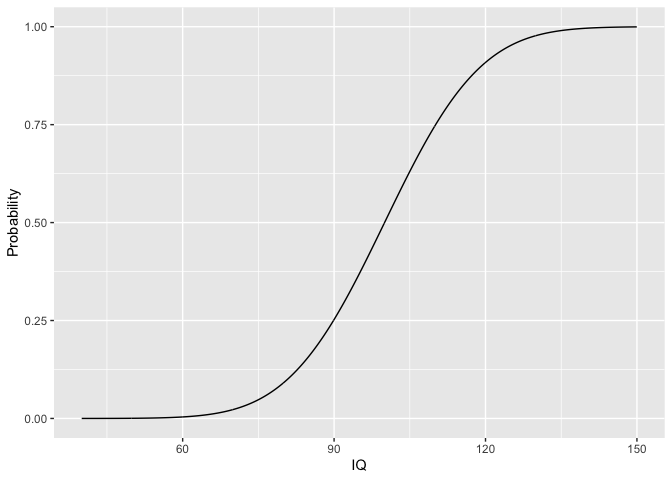
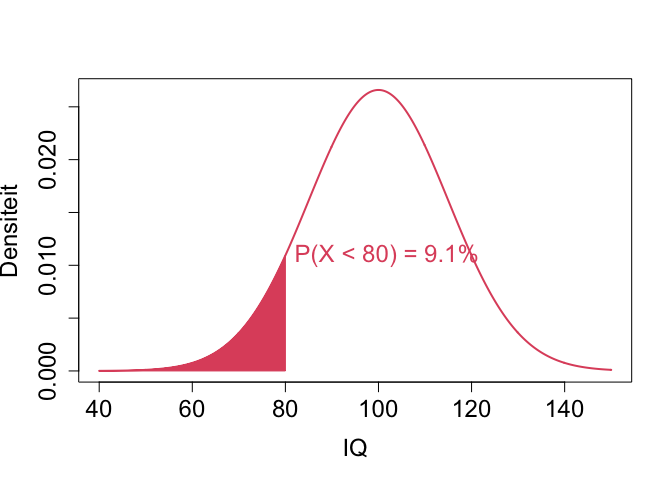
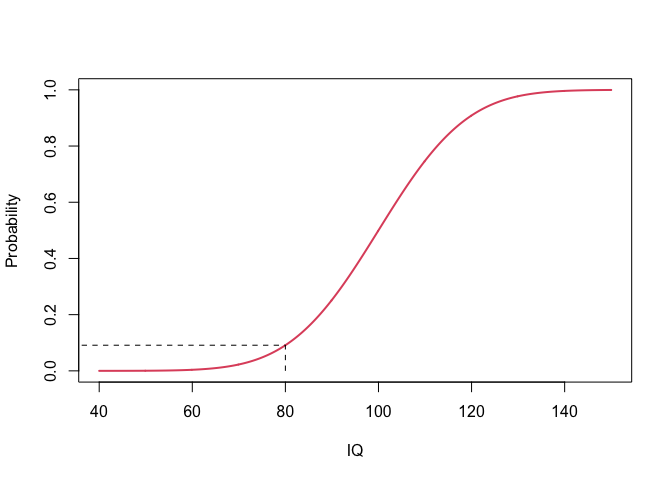
De probabiliteit dat het IQ van een random subject lager is dan 80 wordt in R berekend door

pnorm(80,mean=100,sd=15)

## [1] 0.09121122

Voor de grootst mogelijke waarde voor \(X\) integreren we over de volledige steekproefruimte \(\Omega\) dus

\[\int \limits_{x \in \Omega} f(x) dx=1.\]

De oppervlakte onder de dichtheidsfunctie is dus steeds 1!