A jumble of numbers. As macroeconomic data comes across with most people. Just try to discover an irregularity or mistake. For years, the Greek government, could mislead the EU with its macroeconomic figures. The Greeks had discovered the seemingly perfect fraud: simple to implement and difficult to trace. The government presented its macroeconomic data, but adapted a annoying number here and there. The data was then sent to Eurostat, the European statistics agency, to prove that Greece fulfilled the Stability Pact of the EU. No questions asked, especially since checking macroeconomic data — summaries of complex economic processes — is a very complex task.

However, economists who control national accounts, are getting some unexpected help. A mathematical curiosity, called the law of Benford¹, seems to bring financial irregularities to light - without having to check numbers indefinitely. The law prescribes that in the initial digits of natural numbers intervals can be discovered. A wide range of data, from stocks to surfaces of lakes and primes to bids on eBay, all exhibit the same pattern. Surprisingly often the initial digit of such numbers is a 1, i.e. in about one in three numbers. Slightly less often is the initial digit 2, and even less often 3.

The "natural" distribution of leading digits is defined in detail in the original 1937 article that describes the law of Benford. It states that the probability $$P (c)$$ that a natural number starts with the digit $$c$$ is equal to
\[ P(c) = \log_{10}\left(1 + \frac{1}{c}\right) \]
This probability is graphically shown in the figure below.

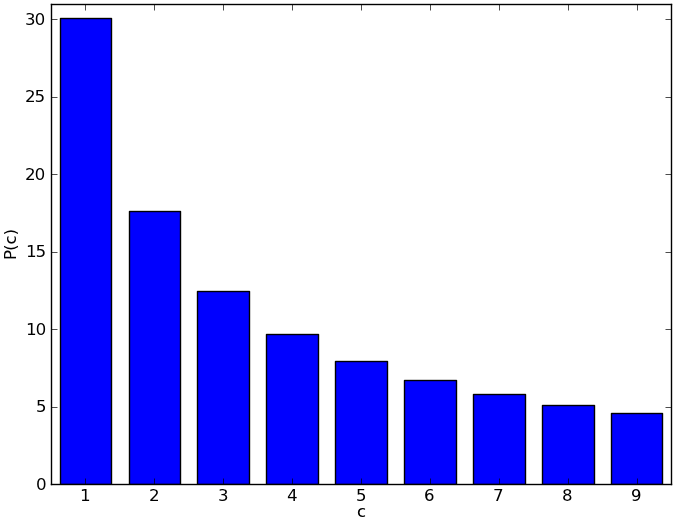
If a series of numbers deviates from this pattern, then the series is unlikely to have come about in a natural way and is possibly adjusted.

Assignment

Write a function benford that returns the theoretical chance $$P(c)$$ that a natural number starts with the digit $$c$$. This chance must be expressed as a percentage. The digit $$c$$ must be passed to the function as an argument.
Write a function readData, to which a file object must be passed as an obligatory argument. This file object must refer to an opened text file, of which all lines contains the same amount of information fields that are separated by one single dash. The function should return a list of integers, that contains the values of a given column of the text file. This column (field numbers are counted from 1) must be passed on as a second obligatory argument. If the given field of the text file contains real numbers, then these have to be rounded off to the closest integer value. Optionally, a third argument can be passed to the function: the dash that is used to separate the information fields in the text file. Use a tab as the default value for this optional argument.
Write a function testBenford that can be used to check if a given list of integer values (that is passed to the function as an argument) meets the law of Benford. For each digit $$c$$ from 1 to 9 the function must print the first digit $$c$$ on a separate line, followed by the theoretical chance $$P(c)$$ (as percentage) that a natural number starts with the digit $$c$$ and the percentage of the integer values in the given list that start with the digit $$c$$. Both percentages are right aligned over 8 positions, and are rounded off to two decimal places.

Example

The file lakes.txt² contains a list of all lakes in the American state Minnesota. Minnesota is sometimes called The Land of 10.000 Lakes, but an official count shows that there are about 11,842 lakes with a surface of 40,000 $$\text{m}^2$$. For each lake, the file contains the following information fields on a separate line, separated by a comma: i) name, ii) county, iii) nearby city, iv) total surface(in acres), v) surface littoral zone (in acres), vi) maximum depth (in feet) and vii) turbidity (in feet). For these data, the law of Benford still applies, as can be concluded from the interactive Python session below (with the surface of the littoral zone as an example).

>>> benford(3)
12.4938736608
>>> benford(7)
5.79919469777

>>> surface = readData('lakes.txt, 5, ',')
>>> surface
[417, 269, 424, 238, 453, 2654, 96, ..., 1953, 367, 432, 345, 387, 89]
>>> testBenford(surface)
1   30.10   31.81
2   17.61   20.55
3   12.49   12.51
4    9.69    9.29
5    7.92    6.61
6    6.69    6.17
7    5.80    5.00
8    5.12    4.47
9    4.58    3.57

Example

The following interactive Python session uses the file inhabitants.txt³. This is the text file that consists of two columns (separated by a tab): i) the name and ii) the number of inhabitants of a state.

>>> data = readData('inhabitants.txt', 2)
>>> data
[33609937, 3639453, 34178188, ..., 48508972, 9059651, 7604467]
>>> testBenford(data)
1   30.10   25.11
2   17.61   16.88
3   12.49   11.69
4    9.69   14.29
5    7.92    5.19
6    6.69    8.23
7    5.80    7.36
8    5.12    6.93
9    4.58    4.33