The Parsons code (formally named the Parsons Code for Melodic Contours) is a simple notation used to identify a piece of music through melodic motion — movements of the pitch up and down. Denys Parsons developed this system for his 1975 book The Directory of Tunes and Musical Themes. Representing a melody in this manner makes it easier to index or search for pieces, particularly when the notes values are unknown.

In the Parsons code, the first note of a melody is denoted with an asterisk (*). All succeeding notes are denoted with one of three letters to indicate the relationship of its pitch to the previous note:

• the letter U (up) when the note is higher than the previous note

• the letter D (down) when the note is lower than the previous note

• the letter R (repeat) when the note has the same pitch as the previous note

These letters are called the movements of the melody. Remark that the difference in pitch between two consecutive notes is ignored in this representation. Below you can see a graphical representation of the Parsons code *RUURDDDDRUURDR of the Ode to Joy¹ theme (original German title: An die Freude) from the Ninth Symphony² of Ludwig van Beethoven³, adopted as the anthem of the European Union.

     * R U U R D D D D R U U R D R

+2         *-*                    
          /   \                   
+1       *     *                  
        /       \                 
 0   *-*         *         *-*    
                  \       /   \   
-1                 *     *     *-*
                    \   /         
-2                   *-*          

If the pitch of the first note is used as a reference (level 0) then this theme moves between two levels below (-2) and two levels above (+2) the reference level. These extreme movements are respectively called the maximum deviation downwards and the maximum deviation upwards.

This representation turns out to be surprisingly effective. Parsons, who spent five years indexing practically every well-known classical theme from the 16th century onward, wrote

I continue to be astonished that such a simple test, taken to the sixteenth note (or less), should be adequate to distinguish more than 10.000 classical themes.

For example, can you identify these classical melodies from their Parsons code? Click here to show the answers.Click here to hide the answers.

Assignment

We represent a Parsons code as a string (str) that starts with an asterisk (*), followed by zero or more occurrences of the letters U, D and R. Parsons codes are treated as case insensitive¹⁸.

A contour plot is a graphical representation of a Parsons code in the form of a rectangular grid. Below you can see an example of such a contour plot for the Parsons code *RUURDDDDRUURDR, where the empty cells represent spaces.

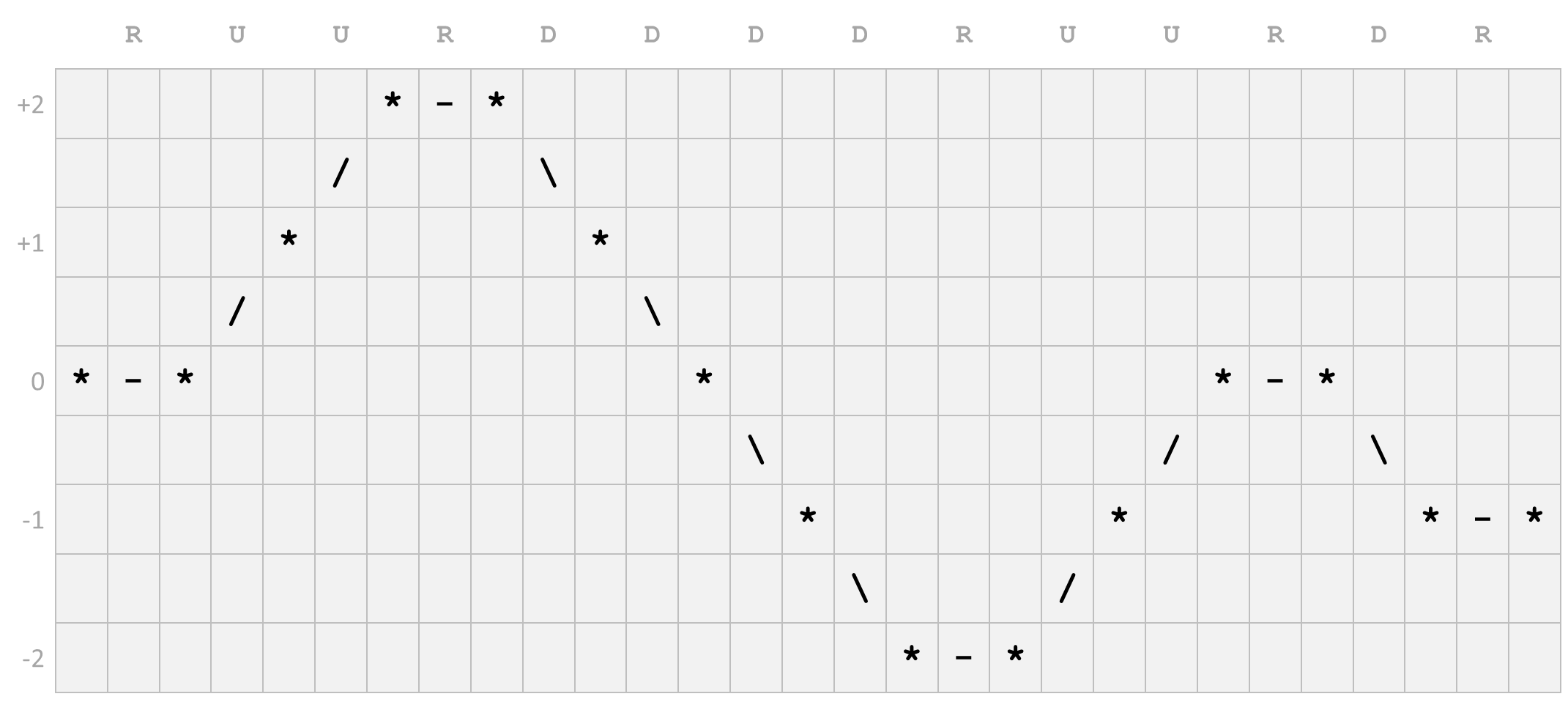
The pitch of the first note is indicated with an asterisk in the first column. Each movement of the Parsons code puts two movement symbols in the next two columns of the grid: with the letter U the symbols / and * are put upwards, with the letter D the symbols \ and * are put downwards and with the letter R the symbols - and * are put on the current row. The grid of the contour plot is chosen so that the first and the last columns respectively correspond to the first and the last notes, and the first and the last rows respectively correspond to the maximum deviation upwards and downwards. Your task:

• Write a function maximum_deviation that takes a Parsons code (str). The function must return a tuple (tuple) containing the maximum deviation downwards (int) and the maximum deviation upwards (int) of the given Parsons code.

• Write a function parsons that takes the location (str) of a text file containing the contour plot of a Parsons code. The function must return the corresponding Parsons code (str) in uppercase letters.

• Write a function contour that takes a Parsons code (str). The function must print the contour plot of the given Parsons code. The function also has a second optional parameter that may take the location (str) of a text file. If a value is explicitly passed to the second parameter, the function must not print the contour plot, but write it to this text file. If the text file did not yet exist, it must be created. If the text file already existed, it must be overwritten.

>>> print('Answer with yes\nope')
Answer with yes\
ope
>>> print('Answer with yes\\nope')
Answer with yes\nope

Example

In the following interactive session we assume the text files parsons_01.txt¹⁹, parsons_02.txt²⁰ and parsons_03.txt²¹ to be located in the current directory.

>>> maximum_deviation('*RUURDDDDRUURDR')
(-2, 2)
>>> maximum_deviation('*uduududdduu')
(-1, 2)
>>> maximum_deviation('*DRRUUDDRUURDUDURDDU')
(-1, 1)

>>> parsons('parsons_01.txt22')
'*RUURDDDDRUURDR'
>>> parsons('parsons_02.txt23')
'*UDUUDUDDDUU'
>>> parsons('parsons_03.txt24')
'*DRRUUDDRUURDUDURDDU'

>>> contour('*RUURDDDDRUURDR')
      *-*                    
     /   \                   
    *     *                  
   /       \                 
*-*         *         *-*    
             \       /   \   
              *     *     *-*
               \   /         
                *-*          
>>> contour('*RUURDDDDRUURDR', 'contour_01.txt25')

>>> contour('*uduududdduu')
        *   *          
       / \ / \         
  *   *   *   *       *
 / \ /         \     / 
*   *           *   *  
                 \ /   
                  *    
>>> contour('*uduududdduu', 'contour_02.txt26')

>>> contour('*DRRUUDDRUURDUDURDDU')
          *         *-*   *   *-*      
         / \       /   \ / \ /   \     
*       *   *     *     *   *     *   *
 \     /     \   /                 \ / 
  *-*-*       *-*                   *  
>>> contour('*DRRUUDDRUURDUDURDDU', 'contour_03.txt27')

Resources

• Parsons D (1975). The Directory of Tunes and Musical Themes. S. Brown. ISBN-13 978-0904747003 ²⁸

• Uitdenbogerd AL, Yap YW (2003). Was Parsons right? An experiment in usability of music representations for melody-based music retrieval. ISMIR. ²⁹