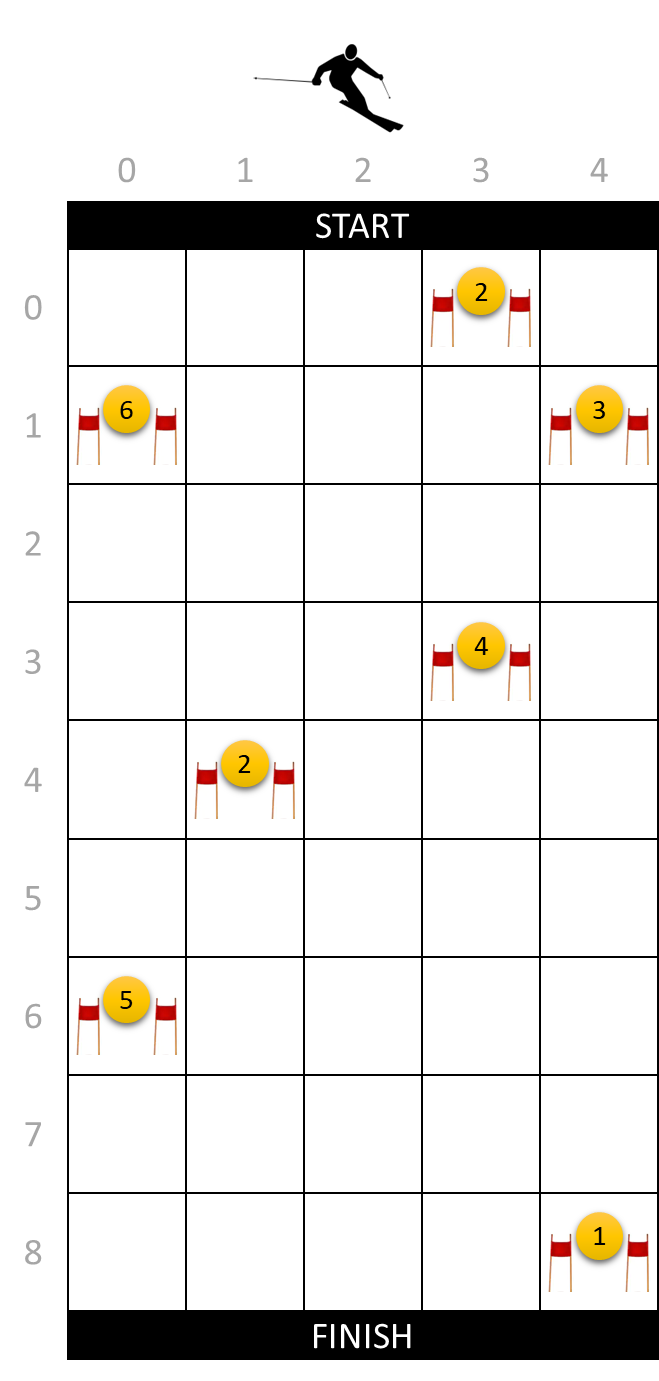
For a slalom competition, the ski slope is divided into a rectangular grid. A number of gates are placed across this grid, each of which is assigned an integer score $$s \in \mathbb{N}_0$$. The rows of the grid are numbered from top to bottom, and the columns from left to right, starting at zero in both cases. This allows us to represent the position of a gate as a tuple $$(r, c)$$, with the row number $$r \in \mathbb{N}$$ and the column number $$c \in \mathbb{N}$$ indicating where the gate is located.

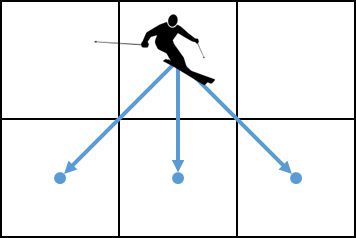
A skier starts at the top (above row 0 of the grid) and can freely choose the position (column) where he starts. With every step the skier always moves

• one row down

• up to one column to the left or to the right

The skier's freedom of movement can therefore be depicted as

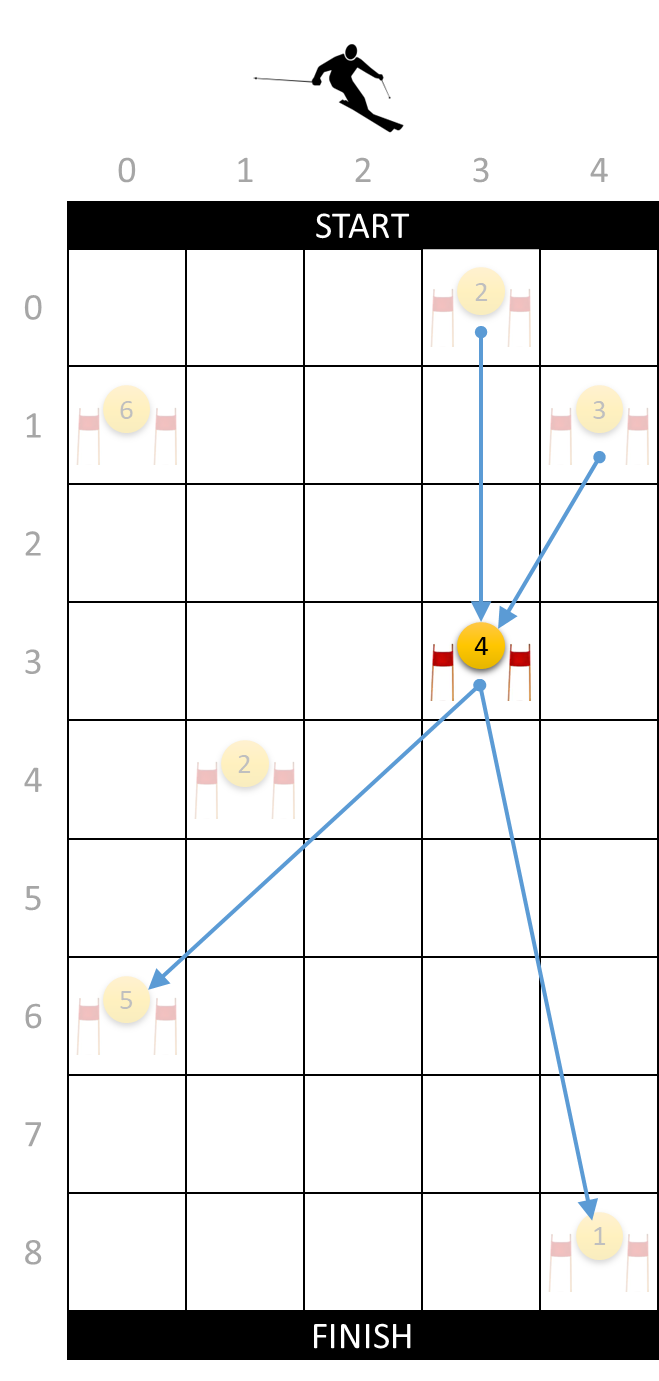
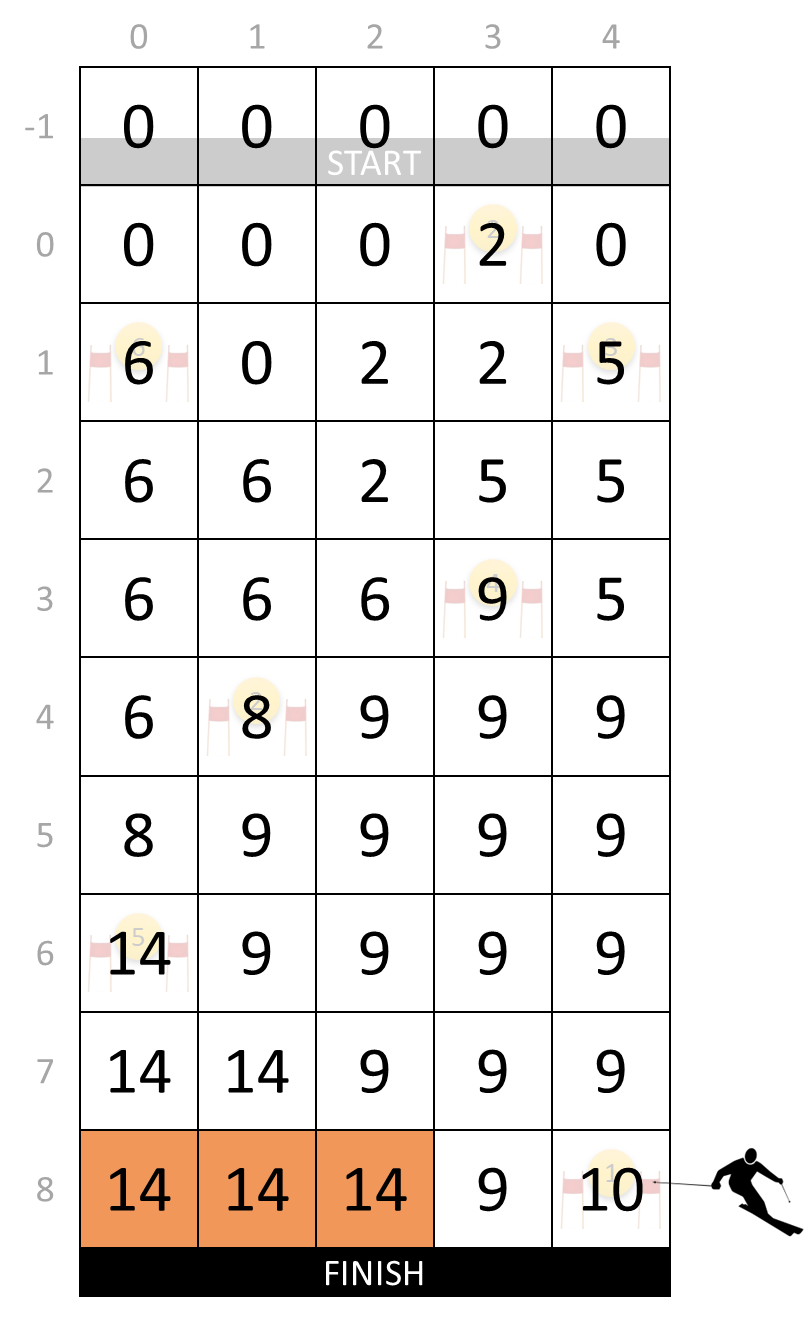
Due to his limited freedom of movement, the skier cannot always follow a course that runs through all the gates on the ski slope. Because he can freely choose his starting position, every gate is reachable from the start, but he cannot necessarily ski from every gate to every other gate. For example, in the left figure below you can see that the gate at position $$(3, 3)$$ is reachable from two higher gates at positions $$(0, 3)$$ and $$(1, 4)$$, and that from this gate only two of the lower gates at positions $$(6, 0)$$ and $$(8, 4)$$ can be reached.

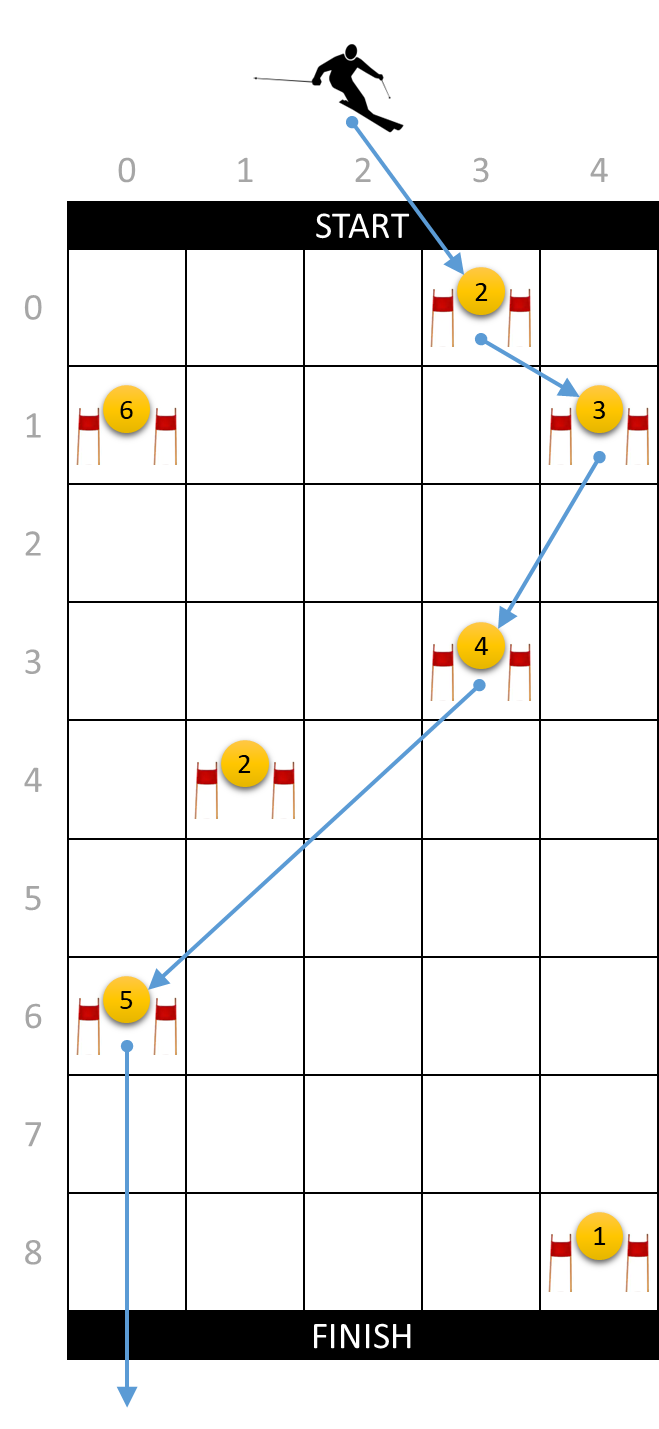
The sum of the scores of all the gates along the course that a skier has followed is called the total score of the course. For a given configuration of a ski slope, we can therefore ask ourselves what maximum total score a skier can get. For the ski slope that we used as an example above, the maximum total score is 14. In the right figure above you see the course the skier must follow to get that total score.

Assignment

Suppose we have a rectangular ski slope with $$m$$ rows and $$n$$ columns, with a number of gates placed across the grid. The following algorithm can be used to find the maximum total score a skier can get on this slope:

1. Initialize a row $$[0, 0, \ldots, 0]$$ with $$n$$ zeros. This row contains the maximum scores in the $$n$$ columns at the start (in row $$-1$$, the row above row $$0$$).

2. Compute the maximum scores in the $$n$$ columns on row $$i$$ ($$i = 0, 1, \ldots, m - 1$$) based on the maximum scores in the $$n$$ columns on the previous row (row $$i - 1$$). The maximum score on row $$i$$ and column $$j$$ ($$j = 0, 1, \ldots, m - 1$$) is the sum of

   • the score of the gate at position $$(i, j)$$ if there is a gate at that position, or $$0$$ otherwise

   • the maximum of three maximum scores in the previous row (row $$i - 1$$), namely in the column to the left of the current column (column $$j - 1$$), in the current column (column $$j$$) and in the column to the right of the current column (column $$j + 1$$); note that we do not necessarily have a column to the left or to the right of the current column at the edges of the ski slope; in those cases we take the maximum over two maximum scores

3. The maximum total score is equal to the maximum of the maximum scores in the bottom row (row $$m  - 1$$).

The following animation shows how this algorithm is applied to the ski slope we used as an example above.

Your task:

• Write a function read_gates that takes the location (str) of a text file that describes the positions of the gates on a ski slope. Each line of the file describes a single gate by three integers $$r$$, $$c$$ and $$s$$, that are separated from each other by a single space. The row number $$r$$ and the column number $$c$$ indicate where the gate is located, and $$s$$ indicates the score of the gate. The function must return a dictionary (dict) that maps the positions $$(r, c)$$ of all gates on the slope onto their score $$s$$ (int).

• Write a function next_row that computes and returns the maximum scores in the $$n$$ columns on row $$i$$, according to the algorithm we described above. The function takes three arguments: i) the row number $$i$$ (int), ii) the maximum scores in the $$n$$ columns in the previous row (row $$i - 1$$) and iii) a dictionary (dict) with the positions and the scores of all gates on the ski slope (formatted like the dictionaries returned by the function read_gates). The maximum scores (int) in the $$n$$ columns on a row are represented as a list.

• Write a function max_total_score that returns the maximum total score (int) a skier can get on a ski slope. The function takes three arguments: i) the number of rows (int) of the ski slope, ii) the number of columns (int) of the ski slope and iii) the location (str) of a text file that describes the positions of the gates on the ski slope (same format as the file passed to the function read_gates).

Example

In the following interactive session we assume the text file slope.txt¹ to be located in the current directory.

>>> gates = read_gates('slope.txt2')
>>> gates
{(0, 3): 2, (1, 0): 6, (1, 4): 3, (3, 3): 4, (4, 1): 2, (6, 0): 5, (8, 4): 1}
>>> next_row(0, [0, 0, 0, 0, 0], gates)
[0, 0, 0, 2, 0]
>>> next_row(1, [0, 0, 0, 2, 0], gates)
[6, 0, 2, 2, 5]
>>> next_row(2, [6, 0, 2, 2, 5], gates)
[6, 6, 2, 5, 5]
>>> next_row(3, [6, 6, 2, 5, 5], gates)
[6, 6, 6, 9, 5]
>>> next_row(4, [6, 6, 6, 9, 5], gates)
[6, 8, 9, 9, 9]
>>> next_row(5, [6, 8, 9, 9, 9], gates)
[8, 9, 9, 9, 9]
>>> next_row(6, [8, 9, 9, 9, 9], gates)
[14, 9, 9, 9, 9]
>>> next_row(7, [14, 9, 9, 9, 9], gates)
[14, 14, 9, 9, 9]
>>> next_row(8, [14, 14, 9, 9, 9], gates)
[14, 14, 14, 9, 10]
>>> max_total_score(8, 5, 'slope.txt3')
14