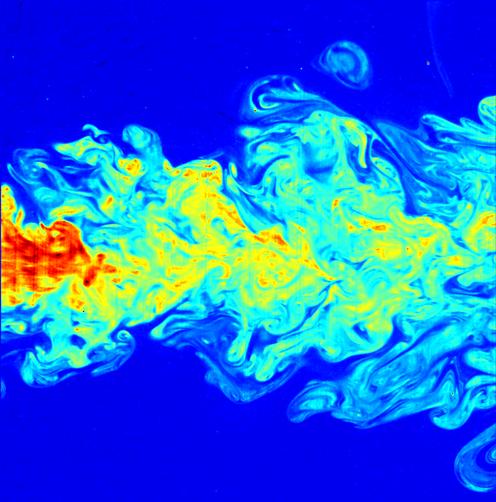
In hydraulics, hydrodynamics and aerodynamics, a distinction is made between laminar and turbulent flows. A laminar flow¹ occurs when a medium (a gas or a fluid) flows in parallel layers, with no disruption between the layers. At low velocities, the medium tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. There are no cross-currents perpendicular to the direction of flow, nor eddies or swirls of fluids. In contrast to laminar flow, turbulent flow² is characterized by chaotic changes in pressure and flow velocity. In general terms, in turbulent flow, unsteady vortexes appear of many sizes which interact with each other, consequently drag due to friction effects increases.

The process of a laminar flow becoming turbulent is known as laminar-turbulent transition. This is an extraordinarily complicated process which at present is not fully understood. However, as the result of many decades of intensive research, certain features have become gradually clear, and it is known that the process proceeds through a series of stages. The moment when laminar flow turns into turbulent flow, and the other way around, is characterized by the dimensionless Reynolds number. The Reynolds number is also used to express the similarity between two flows. This can be useful in studying the behavior of airplane wings or water systems using scale models.

The Reynolds number $$Re$$ is named after Osbourne Reynolds³ (1842-1912) and represents the relation between viscous and inertial forces in the movement a medium makes with regard to an object. \[ Re = \frac{V \cdot L \cdot \rho}{\mu}\, \] Here, $$V$$ [$$\text{m}$$/$$\text{s}$$] is the characterizing speed (in case of flow in a pipe, this is the average flow speed), $$L$$ [$$\text{m}$$] is the characterizing length (in case of flow in a pipe, this is the diameter), $$\rho$$ [$$\text{kg}$$/$$\text{m}^3$$] is the specific mass (density) of the flowing medium and $$\mu$$ [$$\text{Pa} \times \text{s}$$] is the dynamic viscosity of the flowing medium. A low Reynolds number indicates dominant viscous powers that provide a constant, smooth (laminar) flow. A high Reynolds number indicates dominant inertial strength which causes the movement to be chaotic and hard (turbulent flow). The transition (usually transition flow) is different for every geometry.

Input

Four real valued numbers $$V$$, $$L$$, $$\rho$$ and $$\mu$$ that represent the quantities used in the formula of the Reynolds number (expressed in SI units). Each of these numbers is on a separate line.

Output

A real valued number that represents the Reynolds number calculated from the four quantities given in the input. This number is followed on the same line by a space and the type of flow that corresponds to the calculated Reynolds number between round brackets. For Reynolds numbers smaller than 2,000 this is laminar flow, for Reynolds numbers between 2,000 and 4,000 this is transition flow, and for Reynolds numbers larger than 4,000 this is turbulent flow.

Example

Input:

40.2
2.0
991.0
72.0

Output:

1106.616667 (laminar flow)