The elevator paradox is a paradox first noted in the 1950s by Moritz Stern and George Gamow. Both physicists had offices on different floors of a multi-story building. Gamow, who had an office on the second floor of the building, noticed that the first elevator to stop at his floor was most often going down. Stern, who had an office near the top, noticed that the first elevator to stop at his floor was most often going up.

At first sight, it was as if elves were manufacturing elevator cars in the middle of the building and sent them upwards to the roof or downwards to the basement to be dismantled. You can observe the same phenomenon in most tall buildings, and there are no elves involved. Do you see why it occurs?
Suppose you are at one of the bottom floors of a building. In this case, a single elevator spends most of its time in the top section of the building. If we start waiting for an elevator at a random point in time, it will thus be more likely that the first elevator approaches from above and continues downwards. The opposite is true if we are at one of the top floors of the building.
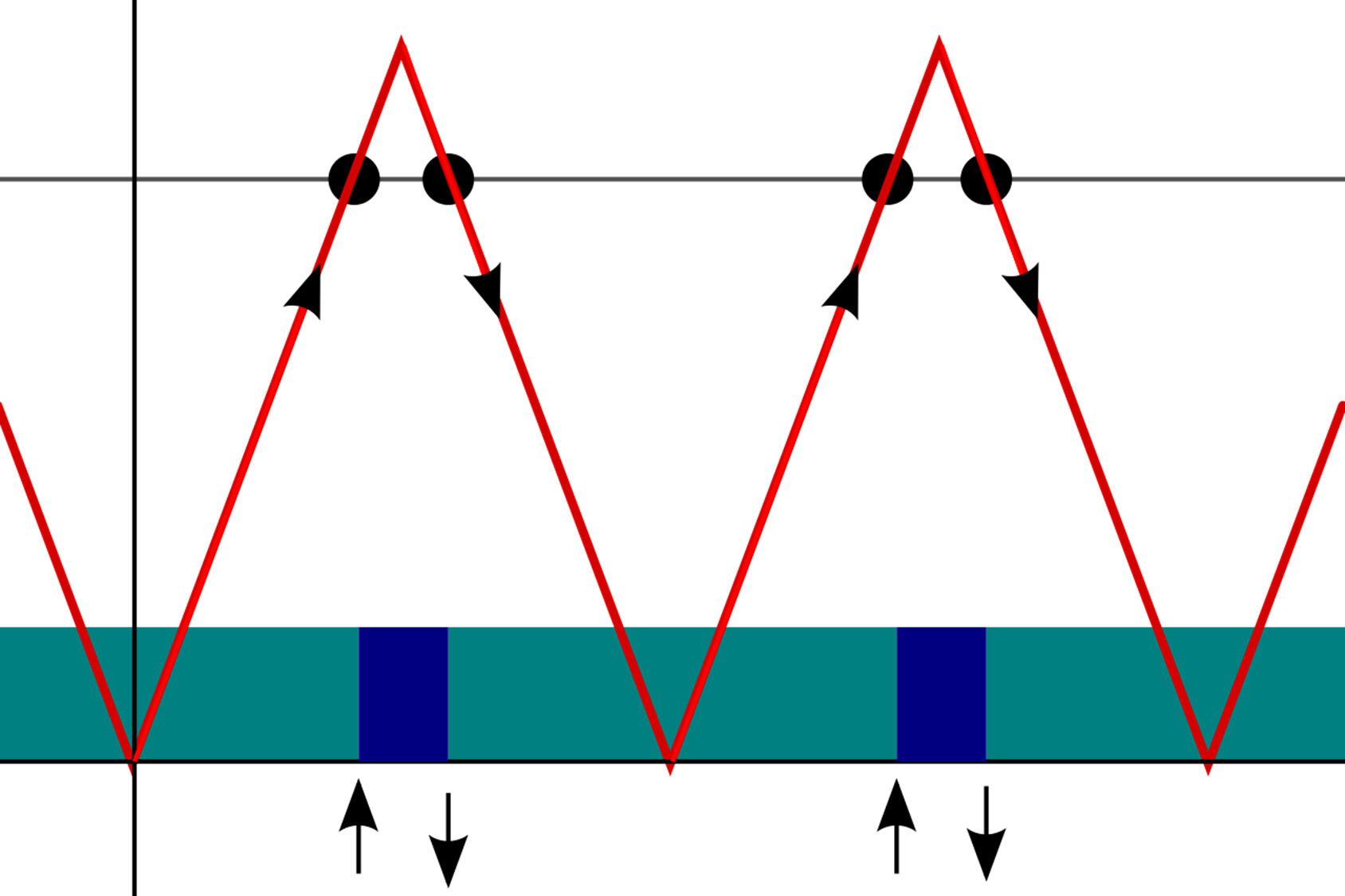
To help visualize this, consider a thirty-story building — plus lobby — with only one slow elevator. The elevator is so slow because it stops at every floor on the way up, and then on every floor on the way down. It takes a minute to travel between floors and wait for passengers. Here is the arrival schedule for people unlucky enough to work in this building. As depicted in the above figure, it forms a triangle wave.
| floor | time on way up | time on way down |
|---|---|---|
| lobby | 8:00, 9:00, … | n/a |
| 1st floor | 8:01, 9:01, … | 8:59, 9:59, … |
| 2nd floor | 8:02, 9:02, … | 8:58, 9:58, … |
| … | … | … |
| 29th floor | 8:29, 9:29, … | 8:31, 9:31, … |
| 30th floor | n/a | 8:30, 9:30, … |
If you were on the first floor and walked up randomly to the elevator, chances are high that the next elevator would be heading down. The next elevator would be heading up only during the first two minutes at each hour, e.g. at 9:00 and 9:01. The number of elevator stops going upwards and downwards are the same, but the odds that the next elevator is going up is only 2 in 60.
Assignment
Generate the arrival schedule for a slow elevator that stops at every floor and takes a minute to travel between floors and wait for passengers. At the start of the simulation, the elevator is at a given floor and moves in a given direction. If the elevator reaches the lobby, it continues going up. If the elevator reaches the top floor, in continues going down.
Input
Seven lines that contain the following information that must be used to simulate the trajectory of the elevator:
-
number of simulated steps ($$\in \mathbb{N}$$); each floor visited by the elevator — including the floor at the start of the simulation — forms a single step in the simulation
-
number $$i \in \mathbb{N}$$ ($$0 \le i \le k$$) of the floor where the simulation starts; lobby is assigned number 0
-
number $$k \in \mathbb{N}_0$$ assigned to the top floor
-
character that indicates whether the elevator goes up or down at the start of the simulation; a caret (circumflex accent; ^) indicates that the elevator initially goes up; a letter v indicates that the elevator initially goes down
-
number of hours on a 24-hour clock at the start of the simulation; for example, 23 if the simulation starts at 23:14
-
number of minutes on a 24-hour clock at the start of the simulation; for example, 14 if the simulation starts at 23:14
-
text that indicates the amount of detail for the output of the simulation; the text verbose indicates that output needs to be generated during each step of the simulation; the text quiet indicates that output only needs to be generated if the elevator visits floor $$i$$
Output
The elevator starts at floor $$i$$ and starts moving in the given direction. For each floor that needs to be included in the arrival schedule, a line must be outputed that contains the current time, the number of the floor that is visited by the elevator, and the direction into which the elevator leaves the current floor (^ if the elevator continues going up, and v is the elevator continues going down). Derive the format of the output from the examples given below. If the last input line contains the text verbose, all floors visited by the elevator during the simulation must be included in the arrival schedule. If the last input line contains the text quiet, only floor $$i$$ at which simulation starts must be included in the arrival schedule.
Example
Input:
30
6
8
^
23
50
verboseOutput:
23:50 6 [^]
23:51 7 [^]
23:52 8 [v]
23:53 7 [v]
23:54 6 [v]
23:55 5 [v]
23:56 4 [v]
23:57 3 [v]
23:58 2 [v]
23:59 1 [v]
00:00 0 [^]
00:01 1 [^]
00:02 2 [^]
00:03 3 [^]
00:04 4 [^]
00:05 5 [^]
00:06 6 [^]
00:07 7 [^]
00:08 8 [v]
00:09 7 [v]
00:10 6 [v]
00:11 5 [v]
00:12 4 [v]
00:13 3 [v]
00:14 2 [v]
00:15 1 [v]
00:16 0 [^]
00:17 1 [^]
00:18 2 [^]
00:19 3 [^]Example
Input:
30
6
8
v
9
30
quietOutput:
09:30 6 [v]
09:42 6 [^]
09:46 6 [v]
09:58 6 [^]