The cells of a rectangular $$m \times n$$ grid with $$m$$ rows and $$n$$ columns each contain a number between 0 and 9. Connected cells containing the same number form a group, where cells are connected if they share a common side (horizontally or vertically). For example, the following $$4 \times 4$$ grid has five groups, marked with a distinct color.

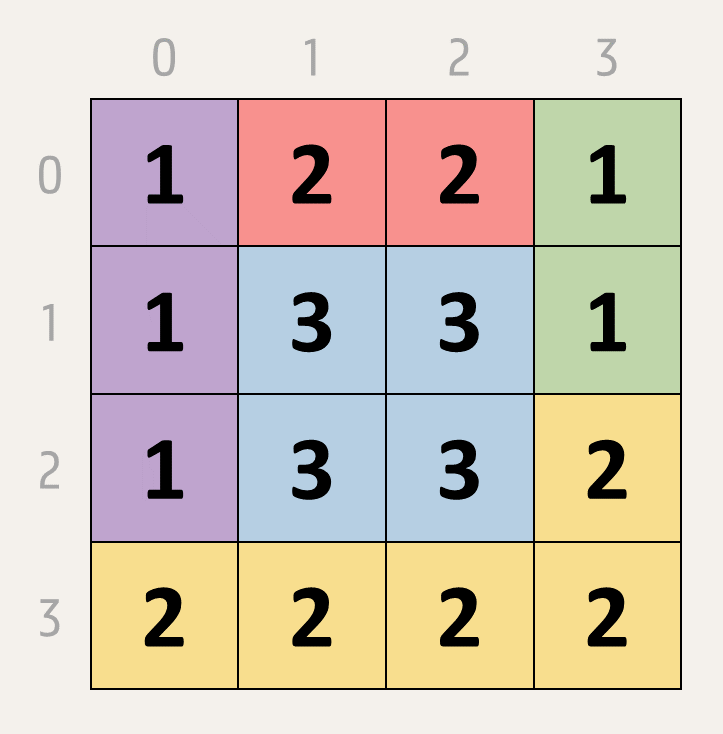
A move increments or decrements all cells in a group by 1, possibly fusing it with other groups. In doing so, the group number may not fall below 0 or exceed 9. The challenge is to fuse the entire grid into a single group using a minimum number of moves. The above example takes just two moves:

• decrement the blue group in the center of the grid, fusing it with the red and yellow groups

• decrement this new larger group, fusing it with the purple and green groups

Assignment

The list representation of a sequence of digits arranged in a rectangular $$m \times n$$ grid consists of a list containing the $$m$$ rows of the grid (top to bottom), where each row is itself represented as a list containing the $$n$$ numbers (int) in the row (from left to right).

The string representation of a sequence of digits arranged in a rectangular $$m \times n$$ grid consists of a tuple containing three elements: i) a string (str) containing the digits as read from left to right and from top to bottom from the grid, ii) the number of rows (int) in the grid and iii) the number of columns (int) in the grid.

We number the rows of the grid from top to bottom and the columns from left to right, each time starting from zero. This way, the position of a cell in the grid can be represented as a tuple $$(r, k)$$, where $$r$$ and $$k$$ indicate the number of the row and the column where the cell is located in the grid.

Your task:

• Write a function list_representation that takes three arguments corresponding to the three separate elements in the string representation of a grid. The third argument may be left out for square grids that have same number of rows and columns. The function must return the list representation of the given grid.

• Write a function string_representation that takes the list representation of a grid. The function must return the string representation of the given grid.

• Write a function move that takes three arguments: i) a number $$\alpha \in \mathbb{N}$$ (int), ii) a set with the positions of some cells in a grid and iii) the list representation of the grid. The function must add the number $$\alpha$$ to all given cells in the grid, and must return a reference to the given grid.

• Write a function is_solved that takes the list representation of a grid. The function must return a Boolean value (bool) that indicates if all cells in the grid contain the same number.

• Write a function group that takes two arguments: i) the position of a cell in a grid and ii) the list representation of the grid. The function must return a set with the positions of all cells in the group containing the given cell.

• Write a function is_solution that takes two arguments: i) a list of moves and ii) the list representation of a grid. Each move is represented as a tuple $$(r, k, b)$$, where $$(r, k)$$ indicates the position of a cell in the group that must be incremented or decremented, and $$b$$ is a Boolean value (bool) that indicates if the group must be incremented (True) or decremented (False). The function must return a Boolean value (bool) that indicates if the moves result in a grid whose cells contain the same number.

The functions string_representation, is_solved, group and is_solution may not modify the given grid. On the other hand, the function move must modify the numbers in the given grid itself and return a reference to the given grid.

Example

>>> grid = list_representation('1221133113322222', 4)
>>> grid
[[1, 2, 2, 1], [1, 3, 3, 1], [1, 3, 3, 2], [2, 2, 2, 2]]
>>> string_representation(grid)
('1221133113322222', 4, 4)
>>> move(-1, {(1, 2), (1, 1), (2, 1), (2, 2)}, grid)
[[1, 2, 2, 1], [1, 2, 2, 1], [1, 2, 2, 2], [2, 2, 2, 2]]
>>> grid
[[1, 2, 2, 1], [1, 2, 2, 1], [1, 2, 2, 2], [2, 2, 2, 2]]
>>> move(+1, {(0, 3), (1, 3)}, grid)
[[1, 2, 2, 2], [1, 2, 2, 2], [1, 2, 2, 2], [2, 2, 2, 2]]
>>> grid
[[1, 2, 2, 2], [1, 2, 2, 2], [1, 2, 2, 2], [2, 2, 2, 2]]
>>> move(+1, {(2, 0), (1, 0), (0, 0)}, grid)
[[2, 2, 2, 2], [2, 2, 2, 2], [2, 2, 2, 2], [2, 2, 2, 2]]
>>> is_solved(grid)
True

>>> grid = list_representation('1221133113322222', 4)
>>> group((2, 1), grid)
{(1, 2), (1, 1), (2, 1), (2, 2)}
>>> group((0, 3), grid)
{(0, 3), (1, 3)}
>>> group((1, 0), grid)
{(2, 0), (1, 0), (0, 0)}
>>> is_solution([(1, 1, False), (3, 2, False)], grid)
True
>>> is_solution([(1, 3, True), (3, 2, False), (0, 1, True)], grid)
False
>>> grid
[[1, 2, 2, 1], [1, 3, 3, 1], [1, 3, 3, 2], [2, 2, 2, 2]]