In the history of science, vis viva (Latin for living force) is an obsolete scientific theory that served as an elementary and limited early formulation of the law of conservation of energy¹. It was the first known description of what we now call kinetic energy² or of energy related to sensible motions. Proposed by Gottfried Leibniz³ over the period 1676–1689, the theory was controversial as it seemed to oppose the theory of conservation of momentum⁴ advocated by Sir Isaac Newton⁵ and René Descartes⁶. The two theories are now understood to be complementary. Leibniz used the term living force to refer to the total kinetic energy of an isolated system⁷.

The theory was eventually absorbed into the modern theory of energy⁸ though the term still survives in the context of celestial mechanics through the vis-viva equation⁹: satellites make an elliptic orbit around the Earth according classic (Newtonian) astrodynamics.

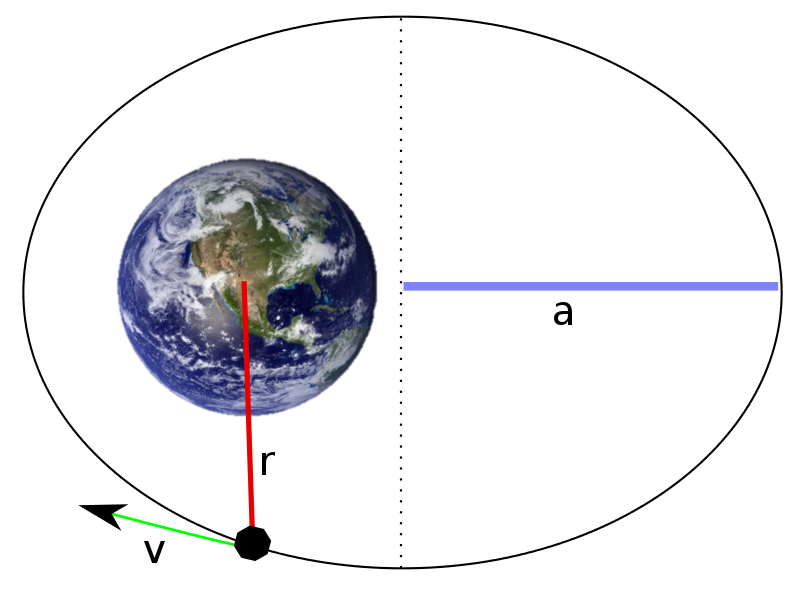
The vis-viva equation relates the semi-major axis $$a$$ of the elliptic orbit, the distance $$r$$ between the satellite and the center of the Earth and the speed $$v$$ of the satellite relative to the Earth: \[ v^2 = \mu \left( \frac{2}{r} - \frac{1}{a} \right) \] The constant $$\mu$$ is the geocentric gravitational constant¹⁰. An approximation of this constant can be computed as the product of the gravitational constant¹¹ $$G$$ and the mass $$M$$ of the Earth expressed in kilograms: \[ \mu = G \cdot M \] However, there are alternative methods to measure the value of $$\mu$$ with greater accuracy by observational astronomy alone. In this assignment we therefore use the more accurate value: \[ \mu = 398600{,}4418 \cdot 10^9\,m^3s^{-2}\] If the length of semi-major axis $$a$$ of the elliptic orbit is known, the period $$p$$ of the satellite can be determined (expressed in seconds): \[ p = 2\pi \sqrt{\frac{a^3}{\mu}}\] The period $$p$$ is the time it takes for the satellite to make a single orbit around the Earth.

Input

Two real-valued numbers, each on a separate line:

• the distance $$r$$ between a satellite and the center of the Earth (expressed in meters)

• the speed $$v$$ of the satellite relative to the Earth (expressed in meters/second)

Output

The given data can be used to compute the length $$a$$ of the semi-major axis of the elliptic orbit the satellite makes around the Earth. This can be done by rewriting the vis-viva equation: \[ a = \frac{\mu r}{2\mu - r v^2} \] The period $$p$$ of the satellite (expressed in seconds) can then be computed as \[ 2\pi \sqrt{\frac{a^3}{\mu}} \]

Three lines of output need to be generated:

• the length $$a$$ of the semi-major axis of the elliptic orbit, expressed in meters

• the length of the period $$p$$, expressed in seconds

• the length of the period $$p$$, expressed as an integer number of days $$d$$, hours $$h$$ and minutes $$m$$ that completely fall within the period; make sure that $$0 \leq h < 24$$ and that $$0 \leq m < 60$$

Take a look at the examples given below to see how the output needs to be formatted.

Example

Satellite: the International Space Station (ISS¹²)

Input:

6792000
7658

Output:

major axis: 6787166.808499204 meters
period: 5564.7257424392155 seconds
period: 0 days, 1 hours and 32 minutes

Example

Satellite: ASTRA 1L¹³, a geostationary satellite which broadcasts BVN¹⁴ among other TV channels

Input:

35785400
3580.9

Output:

major axis: 42160215.133579694 meters
period: 86151.96905571753 seconds
period: 0 days, 23 hours and 55 minutes

Example

Satellite: PROBA-2¹⁵

Input:

7104000
7485

Output:

major axis: 7093371.63898765 meters
period: 5945.52283951033 seconds
period: 0 days, 1 hours and 39 minutes

Example

Satellite: the Moon¹⁶

Input:

400000000
977.75

Output:

major axis: 384375790.60599077 meters
period: 2371619.541180138 seconds
period: 27 days, 10 hours and 46 minutes