A triangle is a geometrical shape that is formed when 3 non-collinear points are joined. The joining line segments are the sides of the triangle. The angles in between the sides on the inside of the triangle are the internal angles.
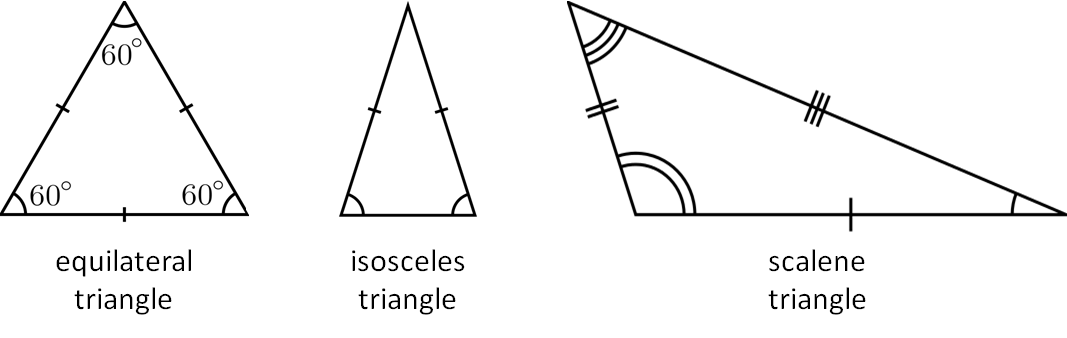
Triangles can be classified according to the length of their sides:
Equilateral triangle: all sides are equal
Isosceles triangle: at least 2 sides are equal in length
Scalene triangle: all sides are unequal
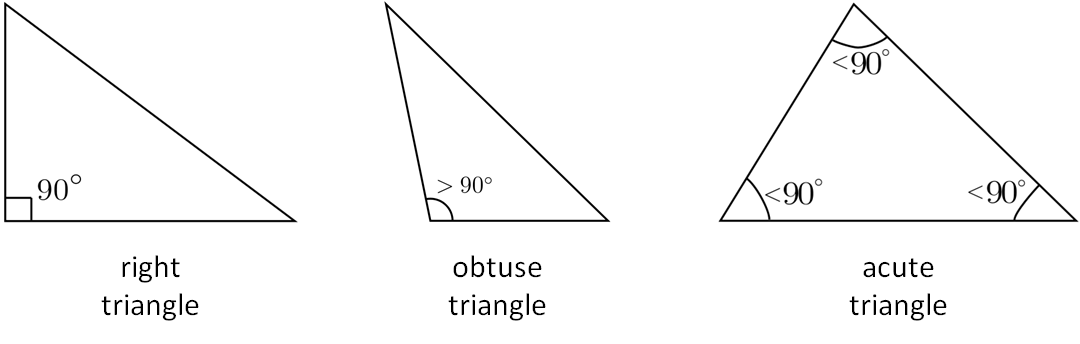
Triangles can also be classified according to their internal angles:
Acute triangle: all interior angles measuring less than 90°
Right triangle: one of its interior angles measures 90°
Obtuse triangle: one interior angle measuring more than 90°
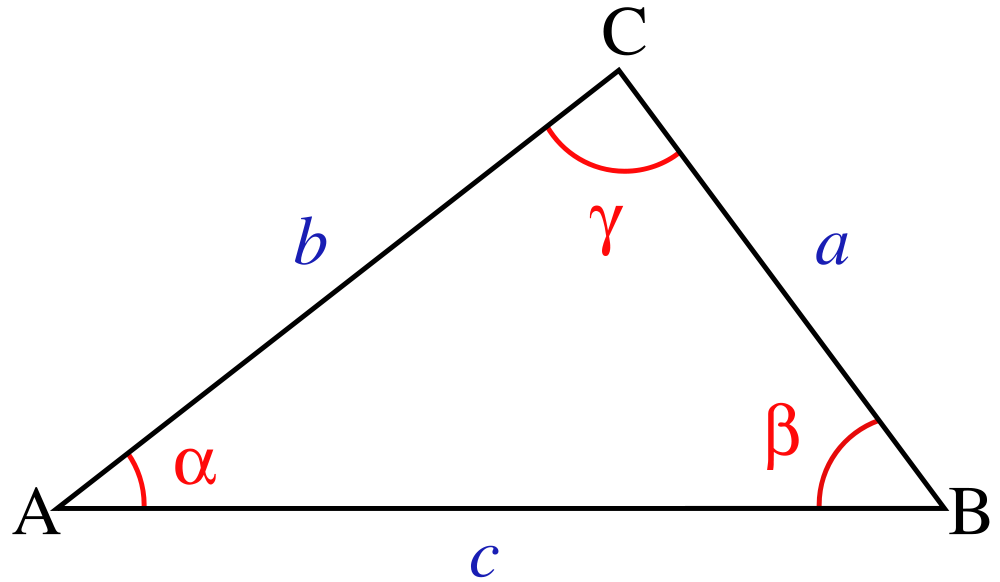
Length of sides between two points
The length $$l$$ of a side that joins the internal angles $$(x_1, y_1)$$ and $$(x_2, y_2)$$ , can be calculated as \[ l = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} \]
Internal angle formed by 2 sides
The size of an internal angle $$\gamma$$ formed by two sides of a triangle can be calculated using the law of cosines $$$cos(\gamma) = \frac{a^2+b^2-c^2}{2ab}$$. $$ , $$a$$ and $$b$$ represent the length of the sides that form the internal angle $$\gamma$$ , $$c$$ represents the length of the side right across the internal angle $$\gamma$ .
Comparing floating point
numbers
For this assignment you have to compare the length of the sides with the size of the angles. Take into consideration that these figures are represented by floating point numbers. When inserted in a computer memory, minor mistakes in rounding off may occur. It is possible that a variable angle representing a 90° angle, has an actual value of 90.00000001. Therefore, testing an angle as follows is a bad idea:
if angle == 90:
print('right angle')Instead, the condition can be reformulated by stating that the size of the corner has to be "in a close range" from 90°. In the code fragment below, an angle may not deviate from 90° by more than 0.000001:
if abs(angle - 90) < 1e-6:
print('right angle')Watch this video1 containing further explanation about working with floating point numbers.
Assignment
Determine the name of the triangle formed by three non-collinear points, based both on its sides as well as on its internal angles.
Input
Six real numbers, each on a separate line. Every pair of consecutive numbers represents the $$(x, y)$$ co-ordinate for an internal angle of a triangle. You may presume that these internal angles are non-collinear.
Output
The name of the triangle that is formed by three points of which the co-ordinates are stated in the input. Use the template Triangle classification: classification_sides classification_angles. Here classification_sides is the term that represents a triangle classified according to the length of its sides. classification_angles is the term that represents a triangle classified according to the size of its internal angles. Always give the most specific term that applies to the triangle.
Example
Input:
-5.018651714882998
5.273815977515895
-4.1327268984230505
5.7376448463677665
-4.596555767274922
6.623569662827715Output:
Triangle classification: isosceles right