Lunar phase or phase of the moon refers to the shape of the illuminated (sunlit) portion of the Moon as seen by an observer, usually on Earth. The lunar phases change cyclically as the Moon orbits the Earth, according to the changing relative positions of the Earth, Moon, and Sun. The half of the lunar surface facing the Sun is always sunlit, but the portion of this illuminated hemisphere that is visible to an observer on Earth can vary from about 100% (full moon) to 0% (new moon). The lunar terminator is the boundary between the illuminated and unilluminated hemispheres. The period of the Moon orbiting the Earth is usually subdivided into eight lunar phases: new moon, waxing crescent, first quarter, waxing gibbous, full moon, waning gibbous, last quarter and waning crescent. If you can determine for a give date how many days have passed since the latest new moon, then the corresponding lunar phase may be determined by looking in which eighth of the period of the lunar rotation this number of days falls (see figure below).

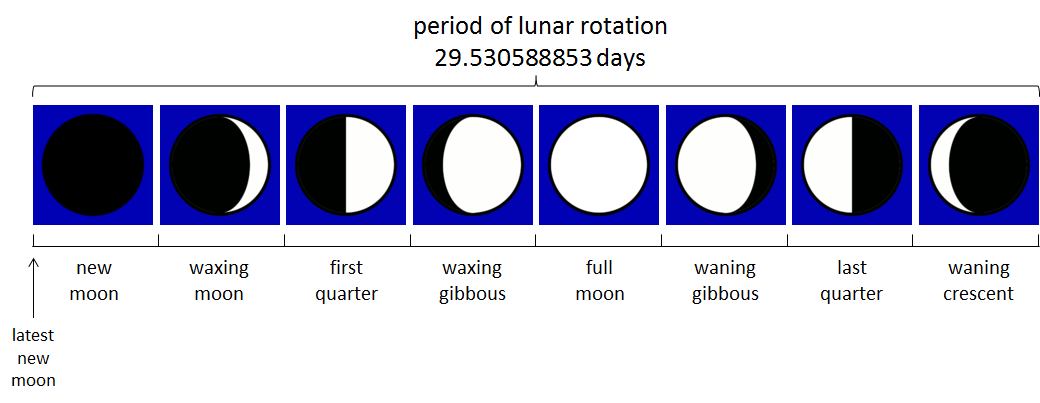
The Moon orbits the Earth with a period of $$p=29.530588853$$ days. If we know that there was a new moon at January 6, 2000, then we can use the following formula to determine the number of days since the last new moon. This number of days will be denoted as $$d_n$$. \[ d_n = d_r - p * \left\lfloor\frac{d_r}{p}\right\rfloor \] Here, $$d_r$$ represents the number of days since the reference day January 6, 2000, and the operator $$\lfloor x\rfloor$$ determines the integer fraction of the floating point number $$x$$. Say, for example, that we want to determine the lunar phase on 28/01/2010. On this day, 3675 days have passed since January 6, 2000, so that $$d_n=13,21$$. Since the value $$d_n$$ falls within the fourth part of the eight-part division of the moon rotation period, this date corresponds to the lunar phase waxing gibbous.

Assignment

Write a function

lunarPhase([day][, month][, year])

that returns the name of the lunar phase corresponding to the given date. The day, the month and the year of the given date must be passed as three separate integer arguments to the function. All parameters of the function are optional, and by default get the value of today's day, month and year respectively. The current date must be determined dynamically, and should not be fixed for example to the date the function was implemented. If the function is called for example with arguments corresponding to the date of January 28th, 2010, the function must return the string waxing gibbous. Try to keep the number and the expression of the conditions that need to be tested in order to compute the result of the function as small as possible.

Hint: Take a look at the datetime module that is part of The Python Standard Library¹. In particular, take a look at what can be done with date objects — representing dates — and timedelta objects — representing time intervals. The following demo contains some clues on how these modules can be used to solve this assignment.

>>> from datetime import date
>>> today = date.today()
>>> type(today)
<type 'datetime.date'>
>>> today.year, today.month, today.day
(2011, 11, 18)
>>> birthday = date(1975, 12, 5)
>>> interval = today - birthday
>>> type(interval)
<type 'datetime.timedelta'>
>>> interval.days
13132
>>> 'Today I am {} days old'.format(interval.days)
'Today I am 13132 days old'

Example

>>> from datetime import date
>>> today = date.today()
>>> print(today)
2011-11-02
>>> lunarPhase(today.day, today.month, today.year)
'waxing moon'
>>> lunarPhase(2, 11, 2011)
'waxing moon'
>>> lunarPhase(day=2, month=11, year=2011)
'waxing moon'
>>> lunarPhase(year=2011, month=11, day=2)
'waxing moon'
>>> lunarPhase(month=11, day=2, year=2011)
'waxing moon'
>>> lunarPhase(2, year=2011, month=11)
'waxing moon'
>>> lunarPhase(month=8)
'new moon'
>>> lunarPhase(month=2)
'waning gibbous'
>>> lunarPhase(year=2020)
'full moon'
>>> lunarPhase(28, 1, 2009)
'new moon'
>>> lunarPhase(28, 1, 2010)
'waxing gibbous'
>>> lunarPhase(28, 1, 2011)
'last quarter'