Rock-paper-scissors is a famous zero-sum1 hand game played between two people. It is often used as a choosing method in a way similar to coin flipping, drawing straws, or throwing dice. It is impossible to gain an advantage over a truly random opponent. However, by exploiting the weaknesses of non-random opponents, it is possible to gain a significant advantage. Indeed, human players tend to be non-random. As a result, there have been programming competitions for algorithms that play rock-paper-scissors.
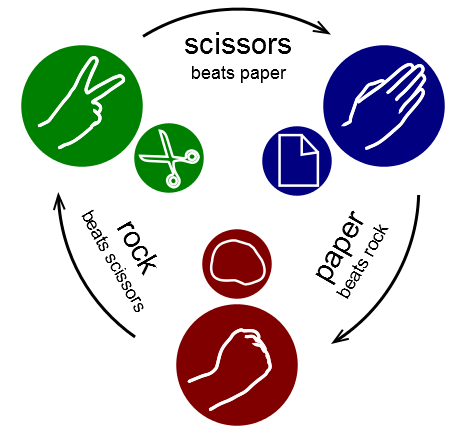
The game goes as follows. The players count aloud to 3, or speak the name of the game (e.g. "Rock! Paper! Scissors!"), each time either raising one hand in a fist and swinging it down on the count or holding it behind. Each player then simultaneously forms one of three shapes with an outstretched hand. These shapes are "rock" (a simple fist), "paper" (a flat hand) and "scissors" (a fist with the index and middle fingers extended, forming a V). Being a zero-sum game, it only has two possible outcomes other than a tie: one of the two players wins, and the other player loses. A player who decides to play rock will beat another player who has chosen scissors ("rock crushes scissors"), but will lose to one who has played paper ("paper covers rock"). A play of paper will lose to a play of scissors ("scissors cut paper"). If both players choose the same shape, the game is tied and is usually immediately replayed to break the tie.

Input
Two lines that each contain one of three possible words: rock, paper or scissors. The first line describes the hand sign formed by player 1, and the second line is the hand sign formed by player2.
Output
A single line that indicates which player wins the game. This line must contain one of the following descriptions:
-
tie
-
player1 wins
-
player2 wins
Try to minimize the total number of conditions that need to be tested to determine the result.
Example
Input:
scissors
rockOutput:
player2 winsEpilogue
A puzzle designed by Yoshinao Katagiri and Nob Yoshigahara.
Andy and Bob play rock-paper-scissors 10 times. Andy plays 3 rocks, 6 scissors, and 1 paper (in some order), and Bob plays 2 rocks, 4 scissors, and 4 paper. There are no ties. Who wins?

If there were no ties, then Andy's 6 scissors used up all of Bob's non-scissors plays (2 rocks and 4 paper). That means that Bob's remaining plays, 4 scissors, were used against Andy's 3 rocks and 1 paper:
| Andy | Bob | winner |
|---|---|---|
| 6 scissors | 2 rocks | Bob (2) |
| 4 papers | Andy (4) | |
| 3 rocks | 4 scissors | Andy (3) |
| 1 paper | Bob (1) |
As such, Andy won 7 out of 10 games.
Epilogue
This robot can win rock-paper-scissors 100% of the time thanks to high speed recognition of high speed vision. Cheater. I'd love to see two of these machines compete against each other.