Introduction to RNA folding

Because RNA is single-stranded, you may have wondered if the cytosine and guanine bases bond to each other like in DNA. The answer is yes, as do adenine and uracil, and the resulting base pairs define the secondary structure of the RNA molecule. Recall that its primary structure is just the order of its bases.

In the greater three-dimensional world, the base pairing interactions of an RNA molecule cause it to twist around on itself in a process called RNA folding. When two complementary intervals of bases located close to each other on the strand bond to each other, they form a structure called a hairpin loop (or stem loop).

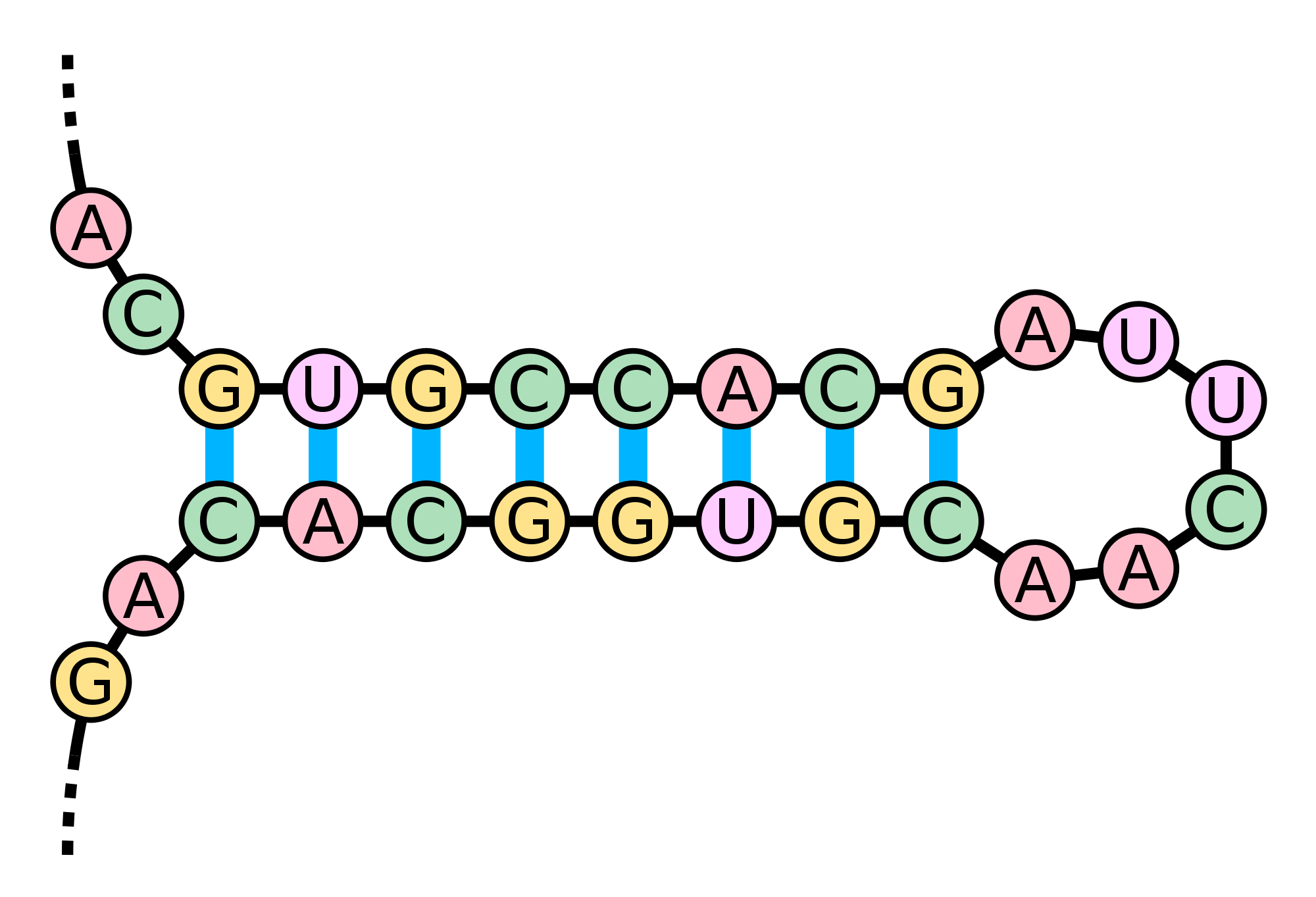
The same RNA molecule may base pair differently at different points in time, thus adopting many different secondary structures. Our eventual goal is to classify which of these structures are practically feasible, and which are not. To this end, we will ask natural combinatorial questions about the number of possible different RNA secondary structures. In this assignment, we will first consider the (impractical) simplified case in which every nucleotide forms part of a base pair in the RNA molecule.

Assignment

A matching in a graph $$G$$ is a collection of edges of $$G$$ for which no node belongs to more than one edge in the collection.

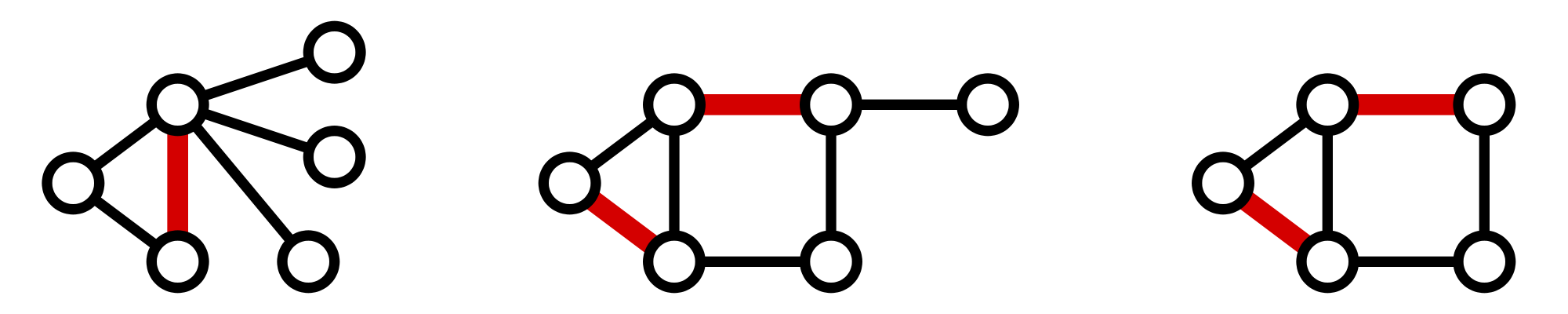
If $$G$$ contains an even number of nodes (say $$2n$$), then a matching on $$G$$ is perfect if it contains $$n$$ edges, which is clearly the maximum possible.

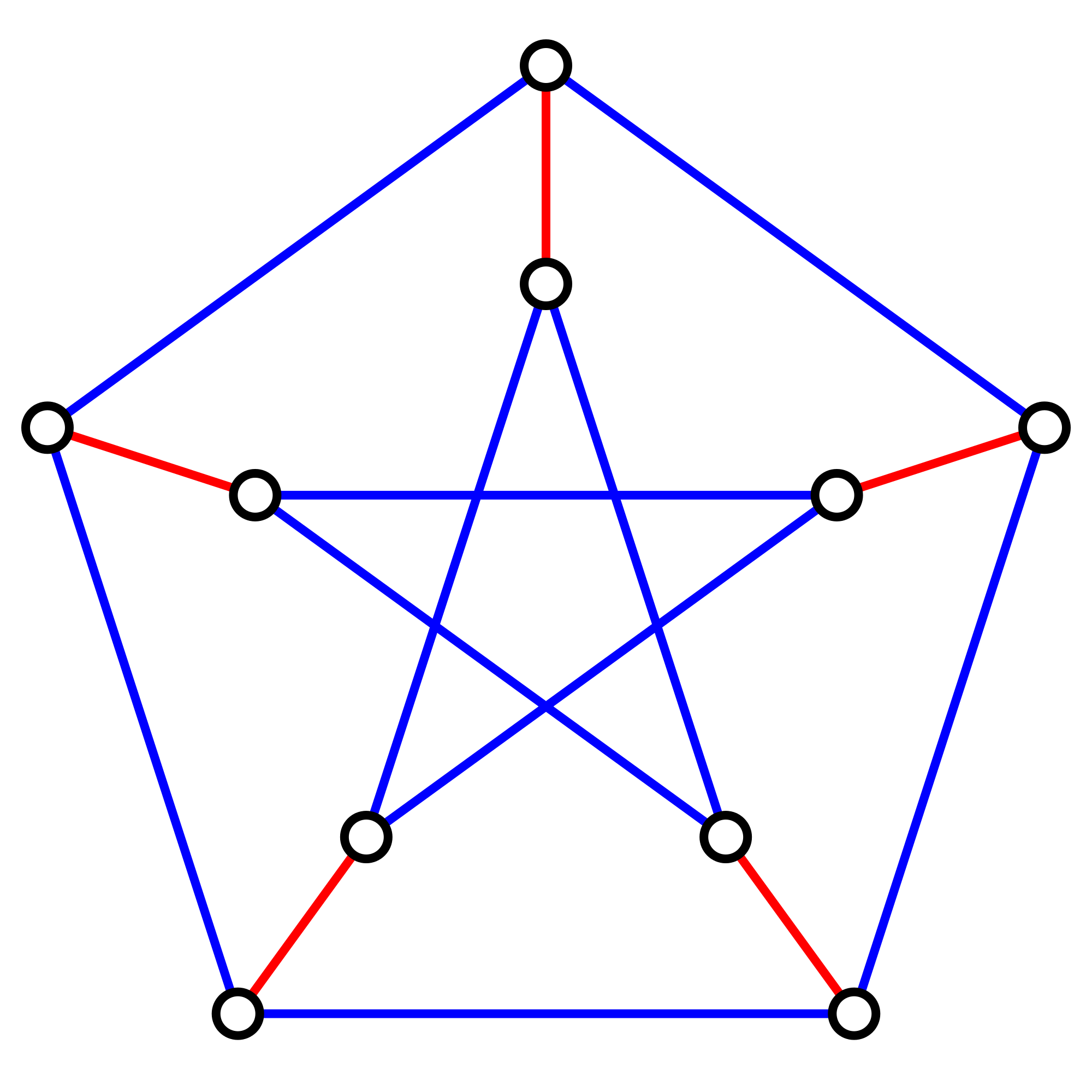
First, let $$K_{2n}$$ denote the complete graph on $$2n$$ labeled nodes, in which every node is connected to every other node with an edge, and let $$p_n$$ denote the total number of perfect matchings in $$K_{2n}$$. For a given node $$x$$, there are $$2n−1$$ ways to join $$x$$ to the other nodes in the graph, after which point we must form a perfect matching on the remaining $$2n−2$$ nodes. This reasoning provides us with the recurrence relation $$p_n = (2n−1)\cdot p_{n−1}$$. Using the fact that $$p_1$$ is 1, this recurrence relation implies the closed equation \[ p_n = (2n−1)(2n−3)(2n−5)\cdots (3)(1) \]

Given an RNA string $$s = s_1s_2\ldots s_n$$, a bonding graph for $$s$$ is formed as follows. First, assign each symbol of $$s$$ to a node, and arrange these nodes in order around a circle, connecting them with edges called adjacency edges. Second, form all possible edges $$\{\mathrm{A}, \mathrm{U}\}$$ and $$\{\mathrm{C}, \mathrm{G}\}$$, called basepair edges. We will represent basepair edges with dashed lines, as illustrated by the bonding graph in the figure below.

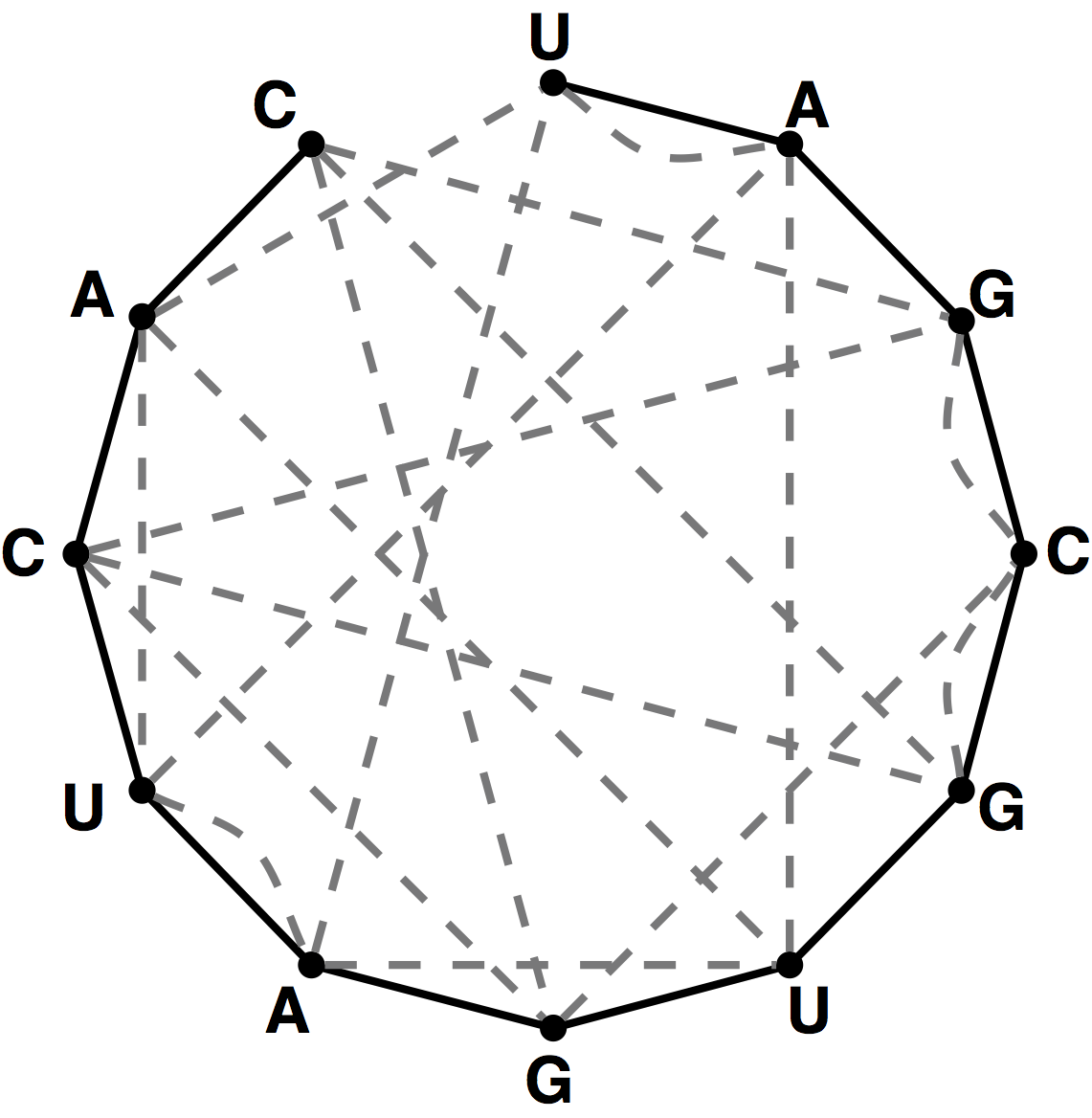
Note that a perfect matching contained in the basepair edges will represent one possibility for base pairing interactions in $$s$$, as shown in the figure below. For such a matching to exist, $$s$$ must have the same number of occurrences of A as U and the same number of occurrences of C as G.

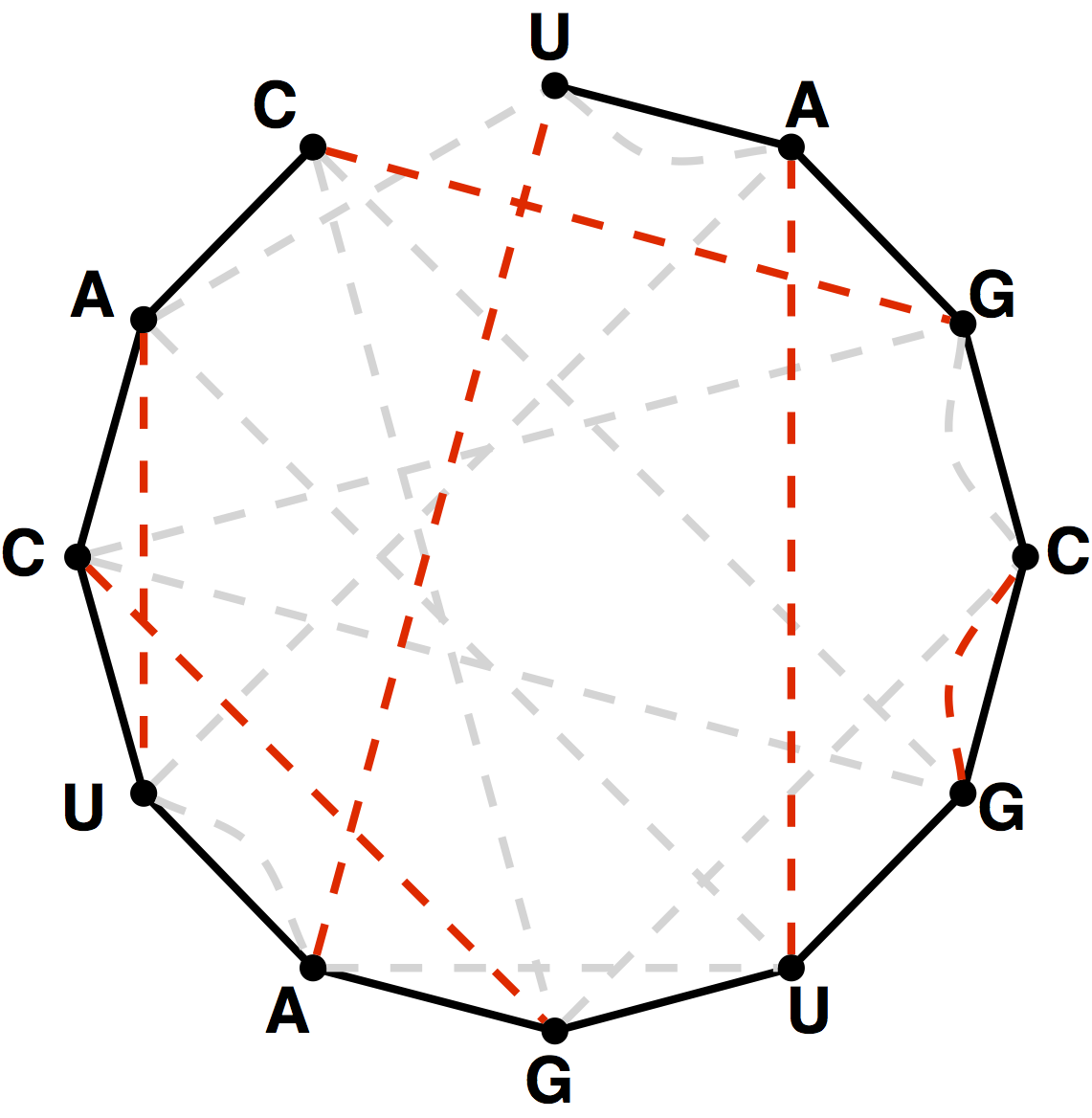
Write a function perfectMatchings that takes an RNA string $$s$$ having the same number of occurrences of A as U and the same number of occurrences of C as G. The function must return the total possible number of perfect matchings of basepair edges in the bonding graph of $$s$$.

Example

>>> perfectMatchings('AGCUAGUCAU')
12
>>> perfectMatchings('GAUCGGUGCGACACAUAUACUCACGGUCGUAGAACGCCUUAGCCGGGCAUUUCCUUAAACUGCCUAGCAAUGAGGGUU')
295950609069496384270872084480000000